
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие о задачах нелинейного программирования
Задачами нелинейного программирования называются задачи математического программирования, в которых нелинейны и (или) целевая функция, и (или) ограничения в виде неравенств или равенств.
Задачи нелинейного программирования можно классифицировать в соответствии с видом функции F(x), функциями ограничений и размерностью вектора х (вектора решений).
Общих способов решения, аналогичных симплекс-методу линейного программирования, для нелинейного программирования не существует.
В каждом конкретном случае способ выбирается в зависимости от вида функции F(x).
Задачи нелинейного программирования на практике возникают довольно часто, когда, например, затраты растут не пропорционально количеству закупленных или произведённых товаров.
Многие задачи нелинейного программирования могут быть приближены к задачам линейного программирования, и найдено близкое к оптимальному решению. Встречаются задачи квадратичного программирования, когда функция есть F(x) полином 2-ой степени относительно переменных, а ограничения линейны. В ряде случаев может быть применён метод штрафных функций, сводящей задачу поиска экстремума при наличии ограничений к аналогичной задаче при отсутствии ограничений, которая обычно решается проще.
Но в целом задачи нелинейного программирования относятся к трудным вычислительным задачам. При их решении часто приходится прибегать к приближенным м етодам оптимизации. Мощным средством для решения задач нелинейного программирования являются численные методы. Они позволяют найти решение задачи с заданной степенью точности.
Общая формулировка нелинейных задач:
Найти переменные х1 , х2, …, хn, удовлетворяющие системе уравнений
| Ψ (х1 , х2, …, хn) = bi , i = 1, 2, …, m | (2.24) |
и обращающие в максимум (минимум) целевую функцию
| Z = f (х1 , х2, …, хn) | (2.25) |
Примером типичной и простой нелинейной задачи является следующая:
Данное предприятие для производства какого-то продукта расходует два средства в количестве х1 и х2 соответственно. Это факторы производства, например, машины и труд, два различных сырья и т.п., а величины х1 и х2 – затраты факторов производства. Факторы производства впредь будем считать взаимозаменяемыми. Если это «труд» и «машины», то можно применять такие методы производства, при которых величина затрат машин в сопоставлении с величиной затрат труда оказывается больше или меньше (производство более или менее трудоемкое).
Объем производства (выраженный в натуральных или стоимостных единицах) является функцией затрат производства Z = f (х1 , х2). Эта зависимость называется производственной функцией. Издержки зависят от расхода обоих факторов (х1 и х2) и от цен этих факторов (c1 и c2). Совокупные издержки выражаются формулой b = c1 х1 + c2 х2. Требуется при данных совокупных издержках определить такое количество факторов производства, которое максимизирует объем продукции Z.
Математическая модель этой задачи имеет вид: определить такие переменные х1 и х2, удовлетворяющие условиям
| c1 х1 + c2 х2 = b | (2.26) |
| х1 ≥ 0, х2 ≥ 0, | (2.27) |
при которых функция
| Z = f (х1, х2) | (2.28) |
достигает максимума. Как правило, функция (2.28) может иметь произвольный нелинейный вид.
Использую классические методы оптимизации, следует четко представлять себе различие между локальным экстремумом функции, глобальным экстремумом и условным экстремумом. Понятие условного экстремума вводится для случая, когда число переменных n не меньше 2 (n ≥ 2). Будем полагать, что функция Z = f (х1 , х2, …, хn) = f (X) дважды дифференцируема в точке Х* = (х1 *, х2 *, …, хn*), (Х* € D(f)) и в некоторой ее окрестности.
Если для всех точек Х этой окрестности f (X*) ≥ f (X) или f (X*) ≤ f (X), то говорят, что функция f (X) имеет экстремум в X* (соответственно максимум или минимум).
Точка X*, в которой все частные производные функции Z = f (Х) равны 0, называется стационарной точкой.
Необходимое условие экстремума.
Если в точке X* функция Z = f (Х) имеет экстремум, то частные производные функции в этой точке равны 0:
f 'x1 (X*) = 0, i = 1, 2,..., n.
Следовательно, точки экстремума функции Z = f (Х) удовлетворяют системе уравнений:
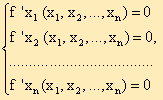
| (2.29) |
Для получения достаточных условий следует определить в стационарной точке знак дифференциала второго порядка. Дифференциала второго порядка обозначается d2f (х1 , х2, …, хn ) f 'x1 (X) найти частную производную по переменной хj, то получим частную производную второго порядка по переменным хi , хj, которая обозначается f ''xi, xj (X). В этом случае
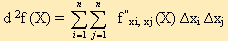
Достаточные условия экстремума.
Двух переменных:
- если Δ > 0 и а11 < 0 (а22 < 0), то в точке Х 0 функция имеет максимум:
если Δ > 0 и а11 > 0 (а22 > 0),то в точке Х 0 – минимум (в этих случаях Х 0 = Х*); - если Δ < 0, то экстремума нет;
- если Δ = 0, то вопрос об экстремуме остается открытым.
· 29. Основы теории массового обслуживания.
· Интенсивное и широкомасштабное использование различных технических устройств привело к необходимости появления специализированных организаций и предприятий, предназначенных для профилактики, ремонта и проведения других работ по поддержанию их работоспособности. Примерами таких обслуживающих структур являются сервисные центры, станции технического обслуживания и ремонтные мастерские, состоящие из некоторого числа подсистем, каждую из которых можно считать каналом обслуживания. В число подобных каналов могут входить различные автоматические устройства и бригады людей, выполняющих определенные заказы или функции.
· Упомянутые структуры иногда выделяют в специализированную отрасль, которую называют системой массового обслуживания, и ее работу уподобляют обслуживанию поступающего потока заявок-требований на выполнение конкретных услуг. Подобные заявки появляются одна за другой в некоторые, вообще говоря, случайные моменты; их обслуживание требует какого-то времени, после чего освободившийся канал снова готов для удовлетворения очередного требования. Так как каждая система массового обслуживания обладает определенной пропускной способностью и ограниченным числом каналов, то возникла необходимость в установлении зависимостей между перечисленными выше ее свойствами и характером потока входящих заявок.
· Установлением подобных зависимостей и иных закономерностей функционирования рассматриваемых здесь систем занимается теория массового обслуживания, а в качестве характеристик их результативности в ней применяют различные показатели и параметры:
· • средний процент требований, покидающих систему необслуженными;
· • среднее время простоя отдельных каналов и системы в целом;
· • среднее время ожидания заявки в очереди на обслуживание;
· • вероятность немедленного приема требования к обслуживанию;
· • закон распределения длины очереди заявок на обслуживание и т.д.
· Нетрудно понять, что все эти характеристики отражают степень приспособленности системы к обслуживанию потока требований, иными словами – ее пропускную способность. Под такой способностью обычно понимают среднее число тех заявок, которые система может обслужить в единицу времени, либо среднее отношение числа удовлетворенных требований к количеству поданных в конкретный период. Очевидно, если заявки поступают в точно определенные промежутки времени и их обслуживание занимает известное время, то оценка пропускной способности не представляет трудности. Однако на практике это не так: в потоке требований возникают сгущения и разрежения, чреватые задержками в обслуживании или простоями как отдельных каналов, так и системы в целом.
· Все это подтверждает, что функционирование систем массового обслуживания представляет собой случайный процесс, требующий детального изучения самих этих систем и классификации обрабатываемых ими потоков событий. При этом под такими потоками часто подразумеваются последовательности событий (обычно однородных), происходящих одно за другим в какие-то моменты времени. Если события наступают через строго определенные промежутки времени, то поток принято называть регулярным.
· Наиболее широко в теории массового обслуживания рассматриваются так называемые простейшие (или стационарные пуассоновские) потоки, которые обладают следующими тремя важными свойствами:
· а) ординарность, когда вероятность попадания на элементарный интервал At времени двух и более событий оказывается пренебрежимо малой по сравнению с вероятностью попадания туда одного события;
· б) отсутствие последействия, если для любых не перекрывающихся интервалов времени число событий, попадающих на один из них, не зависит от числа событий, наблюдаемых на всех других;
· в) стационарность, когда вероятность наблюдения того или иного количества событий за интервал времени [t1; t2] зависит лишь от его продолжительности и не зависит от местоположения на оси времени.
· Кратко и последовательно поясним сущность каждого из этих трех довольно важных для практики свойств. Ординарность означает, что заявки приходят поодиночке, а не парами, тройками и т.д. Если же они поступают только парами или тройками, то неординарный поток можно свести к ординарному – рассматривая заявки как поток пар или троек требований. Наиболее существенным является свойство отсутствие последействия, указывающее на независимость друг от друга тех заявок-требований, которые поступают на вход системы массового обслуживания, чего нельзя сказать о ее выходном потоке. Наконец, стационарность предполагает постоянную плотность потока событий.
· Оказывается, что простейший поток играет в теории массового обслуживания особую роль, до некоторой степени аналогичную роли нормального закона в теории вероятностей и закона больших чисел – в математической статистике. Ранее (см. рис. 2.8) было показано, что при суммировании большого числа независимых случайных величин, подчиненных практически любым законам распределения, получается величина, распределенная по нормальному закону. Аналогично можно доказать, что при взаимном наложении (суммировании) большого числа ординарных стационарных потоков с практически любым последействием получается результирующий поток, довольно близкий к простейшему. Ведь условия, которые должны для этого соблюдаться, подобны условиям центральной предельной теоремы: складываемые потоки оказывают на сумму приблизительно равномерно малое влияние.
· Несмотря на сложность соблюдения подобных условий, на практике существуют потоки, которые правомерно рассматривать как простейшие. Действительно, если сложить 4–5 частных потоков Пi, то этого оказывается достаточно для того, чтобы получить суммарный поток ПS, к которому можно относиться уже как к простейшему.
· 
· Рис. 3.4. Иллюстрация плотности распределения простейшего потока событий
· Убедиться в этом можно с помощью нижней прямой на рис. 3.4, а, точки-события которой на оси времени t свидетельствуют о соблюдении требований стационарности, ординарности и отсутствия последействия.
· При этом оказывается, что число событий, попадающих на участок  , распределено по закону Пуассона с математическим ожиданием а = Xt, а вероятность Р m(t) появления за это время ровно т событий определяется по формуле
, распределено по закону Пуассона с математическим ожиданием а = Xt, а вероятность Р m(t) появления за это время ровно т событий определяется по формуле
· 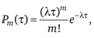
· где λ – плотность потока (среднее число событий, приходящихся на единицу времени).
· Кроме того, нетрудно показать, что промежуток времени между появлением соседних событий простейшего потока подчинен уже упомянутому выше (см. параграф 2.5) экспоненциальному распределению, плотность которого выражается следующей зависимостью:
· 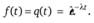
· Оказывается, что экспоненциальный закон (иногда его называют также показательным) обладает еще одним замечательным свойством (рис. 3.4, б): если промежуток времени, распределенный по данному закону, уже длился некоторое время t, то это никак не влияет на закон распределения его оставшейся продолжительности, т.е. он будет таким же, как и закон распределения всего промежутка. Данное свойство представляет собой, в сущности, другую формулировку условия "отсутствие последействия" в простейшем потоке.
· Если же под событиями простейшего потока подразумевать отказы, то это означает, что вероятность их появления в данный момент не зависит от того, сколько времени устройство уже отработало. Это утверждение справедливо для сложных объектов, состоящих из большого числа элементов с разной интенсивностью отказов, но не относится к отказам износового типа. Вот почему простейший поток нашел большое применение в исследованиях надежности, например с помощью так называемых марковских цепей событий, что и будет продемонстрировано ниже (например, при моделировании аварийности и травматизма).
· 
· 
Сетевое планирование и управление
Сетевой моделью (другие названия: сетевой график, сеть) называется экономико-компьютерная модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта (научно-исследовательского, производственного и др.), в их логической и технологической последовательности и связи.
Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет:
во-первых, более четко выявить взаимосвязи этапов реализации проекта;
во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ.
Date: 2015-09-24; view: 1177; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |