
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Мінімальні поліноми
Нехай 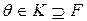 – алгебраїчний над F елемент розширення
– алгебраїчний над F елемент розширення 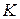 , причому
, причому 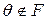 . Нескладно показати, що множина
. Нескладно показати, що множина 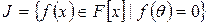 є ідеалом кільця
є ідеалом кільця  , причому
, причому 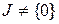 , так як
, так як 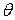 – алгебраїчний елемент. Оскільки
– алгебраїчний елемент. Оскільки  – кільце головних ідеалів, то
– кільце головних ідеалів, то 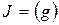 , де g – нормований поліном над F найменшого степеня серед ненульових поліномів, що належать J. Доведемо незвідність g. Оскільки
, де g – нормований поліном над F найменшого степеня серед ненульових поліномів, що належать J. Доведемо незвідність g. Оскільки 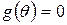 , то
, то 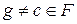 ,таким чином,
,таким чином,  .Припустимо, що поліном g – звідний. Тоді
.Припустимо, що поліном g – звідний. Тоді 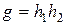 ;
; 
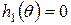 або
або 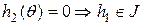 або
або  . Так як
. Так як  , то це входить у протиріччя з мінімальністю степеня
, то це входить у протиріччя з мінімальністю степеня 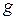 у
у 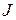 .
.
u Поліном g, що породжує ідеал 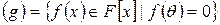 називається мінімальним поліномом елемента q.
називається мінімальним поліномом елемента q.
Вище був розглянутий випадок 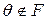 . Для
. Для 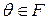 мінімальним буде поліном
мінімальним буде поліном 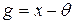 .
.
Отже, кожний алгебраїчний елемент розширення 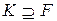 має мінімальний поліном над F.
має мінімальний поліном над F.
u Степінь мінімального полінома елемента q називається степенем цього елемента.
Вищенаведені міркування повністю доводять наступну теорему.
ТЕОРЕМА 22. Нехай 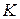 – розширення поля F, елемент
– розширення поля F, елемент 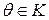 – алгебраїчний над F. Тоді q має мінімальний поліном
– алгебраїчний над F. Тоді q має мінімальний поліном 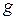 , причому:
, причому:
1) g – незвідний поліном;
2) 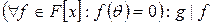 ;
;
3) g є нормованим поліномом мінімального степеня, для якого q є коренем.
ТЕОРЕМА 23. Нехай 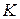 – розширення поля F, елемент
– розширення поля F, елемент 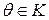 – алгебраїчний над F, g – мінімальний поліном для q,
– алгебраїчний над F, g – мінімальний поліном для q, 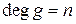 . Тоді:
. Тоді:
1) 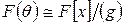 ;
;
2) 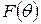 – лінійний векторний простір над F розмірності n, і
– лінійний векторний простір над F розмірності n, і 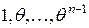 – його базис;
– його базис;
3) будь-який елемент 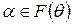 є алгебраїчним над F, причому степінь
є алгебраїчним над F, причому степінь 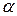 ділить n.
ділить n.
41) Розглянемо відображення 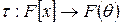 , визначене як
, визначене як
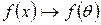 .
.
Тоді 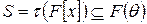 . Очевидно, що t – гомоморфізм. За теоремою про гомоморфізм кілець
. Очевидно, що t – гомоморфізм. За теоремою про гомоморфізм кілець 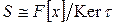 .
. 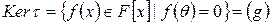 , тобто
, тобто  . Залишилося довести, що
. Залишилося довести, що 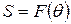 . Оскільки
. Оскільки 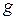 незвідний, то
незвідний, то 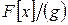 - поле, отже і
- поле, отже і 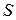 - поле. q входить в S, оскільки
- поле. q входить в S, оскільки 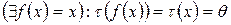 . Але оскільки F і q входять в S, а F(
. Але оскільки F і q входять в S, а F( 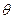 ) – мінімальне поле, що містить F і q, то
) – мінімальне поле, що містить F і q, то 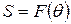 .
.
2) Доведемо, що 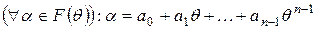 . Маємо:
. Маємо: 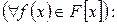
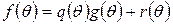 ,
, 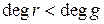 , але
, але 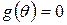 за умовою, тому,
за умовою, тому, 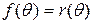 де
де 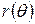 завжди можна представити у вигляді
завжди можна представити у вигляді 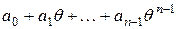 . Залишилося показати, що
. Залишилося показати, що 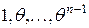 – лінійно незалежна система:
– лінійно незалежна система: 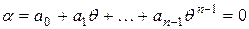 Þ
Þ 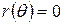 Þ
Þ 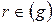 , але
, але 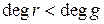 , а
, а 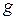 - поліном найменшого степеня в
- поліном найменшого степеня в 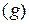 . Отже, залишається лише одна можливість:
. Отже, залишається лише одна можливість: 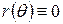 , тобто
, тобто 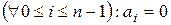 .
.
3) Оскільки F(θ) – скінченне розширення (доведено в п.2), то воно алгебраїчне (див. теор.21). Отже, будь-який його елемент алгебраїчний над F (за означенням), тобто 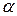 – алгебраїчний над F. За теор.20
– алгебраїчний над F. За теор.20 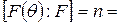
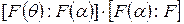 Þ
Þ 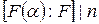 .3
.3
› Надалі, якщо не обумовлене протилежне, розглядатимемо тільки скінченні поля.
Date: 2015-09-18; view: 318; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |