
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основні означення та необхідні відомості з теорії груп та кілець
Л.О. Завадська
ПРИКЛАДНА АЛГЕБРА:
Скінченні поля
Навчальний посібник
 КИЇВ – 2010
КИЇВ – 2010
| УДК | 519.2 |
| ББК | 22.172 (4Укр) |
| К 56 |
ЗМІСТ
1. ОСНОВНІ ОЗНАЧЕННЯ ТА НЕОБХІДНІ ВІДОМОСТІ З ТЕОРІЇ ГРУП ТА КІЛЕЦЬ..........................................................................................4
2. КІЛЬЦЯ ЛИШКІВ ЗА МОДУЛЕМ 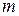 ...........................................................8
...........................................................8
3. КІЛЬЦЯ ПОЛІНОМІВ..................................................................................10
3.1. Поліноми над кільцями....................................................................10
3.2. Поліноми над полями......................................................................13
3.3. Фактор-кільця 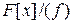 ...................................................................14
...................................................................14
4. КОРЕНІ ПОЛІНОМІВ ТА ЇХ ВЛАСТИВОСТІ..........................................16
5. ПОЛЯ ЧАСТОК.............................................................................................17
6. ПІДПОЛЯ. ПРОСТІ ПОЛЯ. ХАРАКТЕРИСТИКИ ПОЛІВ......................19
7. РОЗШИРЕННЯ ПОЛІВ................................................................................21
8. АЛГЕБРАЇЧНІ РОЗШИРЕННЯ...................................................................23
9. МІНІМАЛЬНІ ПОЛІНОМИ.........................................................................23
10. ПРОСТІ РОЗШИРЕННЯ ПОЛІВ ТА ЇХ ПОБУДОВА............................25
11. ПОЛЯ РОЗКЛАДУ ПОЛІНОМІВ..............................................................27
12. ТЕОРЕМА ПРО ІСНУВАННЯ ТА ЄДИНІСТЬ СКІНЧЕННИХ ПОЛІВ..........................................................................................................27
13. КРИТЕРІЙ ПІДПОЛЯ, ДІАГРАМИ ВКЛЮЧЕННЯ ПІДПОЛІВ...........29
14. МУЛЬТИПЛІКАТИВНА ГРУПА СКІНЧЕННОГО ПОЛЯ....................30
15. НЕЗВІДНІ ПОЛІНОМИ ТА ЇХ КОРЕНІ...................................................32
16. СПРЯЖЕНІ ЕЛЕМЕНТИ............................................................................34
17. ЗОБРАЖЕННЯ ЕЛЕМЕНТІВ СКІНЧЕННИХ ПОЛІВ............................35
18. ПОРЯДКИ ПОЛІНОМІВ............................................................................38
19. ПРИМІТИВНІ ПОЛІНОМИ.......................................................................42
20. СЛІДИ ТА НОРМИ.....................................................................................43
21. БАЗИСИ.......................................................................................................46
22. АВТОМОРФІЗМИ СКІНЧЕННИХ ПОЛІВ..............................................48
23. ЗВЕДЕННЯ ОСНОВНИХ ПОЛОЖЕНЬ ТА РЕЗУЛЬТАТІВ.................50
ПРЕДМЕТНИЙ ПОКАЖЧИК..........................................................................53
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ...................................................55
ОСНОВНІ ОЗНАЧЕННЯ ТА НЕОБХІДНІ ВІДОМОСТІ З ТЕОРІЇ ГРУП ТА КІЛЕЦЬ
Означення відмічатимемо знаком u, початок і кінець доведення – відповідно значками 4та 3, а зауваження – знаком ›.
u Нехай 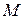 – довільна множина,
– довільна множина, 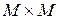 – множина впорядкованих пар
– множина впорядкованих пар 
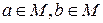 . Відображення
. Відображення 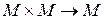 будемо називати (бінарною) операцією на
будемо називати (бінарною) операцією на 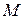 .
.
Таким чином, кожній парі 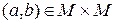 ставиться у відповідність елемент
ставиться у відповідність елемент 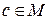 – результат операції:
– результат операції: 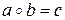 (операцію позначили через
(операцію позначили через 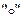 ). Те, що
). Те, що  належить множині
належить множині 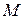 , означає замкненість множини
, означає замкненість множини 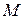 відносно операції
відносно операції 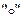 .
.
u Під алгебраїчною структурою будемо розуміти деяку множину 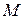 з однією або кількома операціями на ній. Саму множину
з однією або кількома операціями на ній. Саму множину 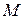 називають при цьому носієм даної алгебраїчної структури.
називають при цьому носієм даної алгебраїчної структури.
u Напівгрупою називається алгебраїчна структура з однією операцією 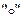 , що задовольняє умові асоціативності:
, що задовольняє умові асоціативності:
 .
.
u Групою  називається алгебраїчна структура з однією операцією
називається алгебраїчна структура з однією операцією 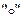 , для якої виконуються умови:
, для якої виконуються умови:
1) операція 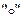 асоціативна;
асоціативна;
2) існує елемент 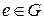 такий, що для будь-якого
такий, що для будь-якого 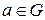
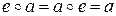
(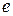 ‑ одиничний або нейтральний елемент);
‑ одиничний або нейтральний елемент);
3) для будь-якого 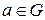 існує елемент
існує елемент 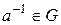 такий, що
такий, що
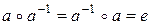
(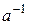 – обернений до
– обернений до 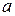 елемент).
елемент).
u Група називається скінченною (відповідно нескінченною), якщо кількість її елементів скінченна (відповідно нескінченна). Кількість елементів скінченної групи називається її порядком.
u Якщо операція в групі  комутативна:
комутативна:
( ,
,
то група  називається абелевою.
називається абелевою.
u Групову операцію можна трактувати як множення, тоді говорять про мультиплікативний запис операції або мультиплікативну групу. Якщо ж операція в групі розуміється як додавання, то групу називають адитивною.
u Мультиплікативна група  назиавється циклічною, якщо в ній існує такий елемент
назиавється циклічною, якщо в ній існує такий елемент 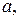 що
що 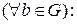
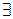 ціле
ціле 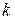 таке, що
таке, що 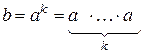 , тобто кожен елемент групи є степенем деякого елемента
, тобто кожен елемент групи є степенем деякого елемента 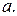 Елемент
Елемент 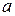 називається твірним елементом групи
називається твірним елементом групи  , а циклічну групу
, а циклічну групу  позначають
позначають 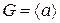 .
.
У разі адитивного запису групової операції має місце те саме означення з заміною степеня 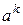 на кратне
на кратне 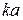 .
.
u Підмножина 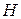 групи
групи  називається підгрупою
називається підгрупою  , якщо
, якщо 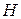 сама утворює групу відносно операції групи
сама утворює групу відносно операції групи  .
.
ТЕОРЕМА (Лагранжа) Порядок підгрупи 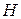 скінченної групи
скінченної групи  ділить порядок
ділить порядок  .
.
u Відображення 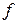 групи
групи  у групу
у групу 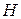 називається гомоморфізмом групи
називається гомоморфізмом групи  у
у 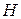 , якщо воно зберігає операцію групи
, якщо воно зберігає операцію групи  . Тобто, якщо
. Тобто, якщо 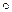 та
та 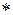 ‑ операції відповідно у групах
‑ операції відповідно у групах  та
та 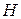 , то
, то 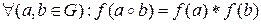 . Якщо, крім того,
. Якщо, крім того, 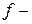 відображення “на”, то
відображення “на”, то 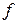 називається епіморфізмом (або гомоморфізмом “на”). Гомоморфізм
називається епіморфізмом (або гомоморфізмом “на”). Гомоморфізм  у
у  називається ендоморфізмом цієї групи. Якщо
називається ендоморфізмом цієї групи. Якщо 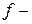 взаємно-однозначний гомоморфізм групи
взаємно-однозначний гомоморфізм групи  на групу
на групу 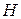 , то він називається ізоморфізмом, і в такому випадку говорять, що групи
, то він називається ізоморфізмом, і в такому випадку говорять, що групи  та
та 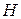 ізоморфні. Ізоморфізм групи
ізоморфні. Ізоморфізм групи  на
на  називається автоморфізмом цієї групи.
називається автоморфізмом цієї групи.
u Кільцем  називається алгебраїчна структура з двома операціями, які умовно назвемо додаванням та множенням. При цьому:
називається алгебраїчна структура з двома операціями, які умовно назвемо додаванням та множенням. При цьому:
1) відносно операції додавання  утворює абелеву групу;
утворює абелеву групу;
(нейтральний елемент цієї групи позначається 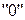 , обернений до
, обернений до 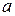 ‑ через
‑ через 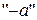 , він називається протилежним до
, він називається протилежним до 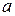 елементом);
елементом);
2) відносно операції множення  утворює напівгрупу;
утворює напівгрупу;
3) операції додавання та множення пов’язані законами дистрибутивності:
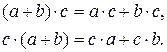
u Якщо в кільці  існує нейтральний елемент за множенням, то
існує нейтральний елемент за множенням, то 
 називається кільцем з одиницею.
називається кільцем з одиницею.
u Якщо операція множення в кільці  комутативна, то
комутативна, то  називається комутативним кільцем.
називається комутативним кільцем.
u Якщо в комутативному кільці  з одиницею
з одиницею 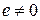 немає дільників нуля, тобто
немає дільників нуля, тобто 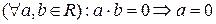 або
або 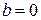 , то
, то  називається областю цілісності або цілісним кільцем.
називається областю цілісності або цілісним кільцем.
В області цілісності можна скорочувати на елементи, відмінні від 0: 
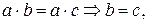
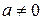 .
.
u Область цілісності  називається евклідовим кільцем, якщо існує таке відображення
називається евклідовим кільцем, якщо існує таке відображення 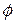 множини ненульових елементів
множини ненульових елементів  у множину невід’ємних цілих чисел, що для будь-яких
у множину невід’ємних цілих чисел, що для будь-яких 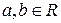 ,
, 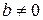 існують елементи
існують елементи 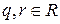 такі, що
такі, що 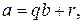 причому
причому 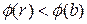 або
або 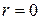 . Іншими словами, в
. Іншими словами, в  можливе ділення з лишком.
можливе ділення з лишком.
Прикладом комутативного кільця з одиницею є множина цілих чисел із звичайними операціями додавання та множення. Це кільце є цілісним, більше того, це евклідове кільце (достатньо визначити  як абсолютну величину числа
як абсолютну величину числа 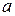 ).
).
u Підмножина 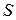 кільця
кільця  називається підкільцем, якщо
називається підкільцем, якщо 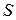 замкнене відносно операцій кільця
замкнене відносно операцій кільця  і
і 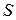 утворює кільце відносно цих операцій.
утворює кільце відносно цих операцій.
› Надалі в цьому параграфі під  будемо розуміти комутативне кільце з одиницею.
будемо розуміти комутативне кільце з одиницею.
u Підкільце 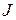 кільця
кільця  називається ідеалом цього кільця, якщо
називається ідеалом цього кільця, якщо 
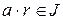 (підкільце
(підкільце 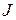 “витримує” множення на всі елементи кільця
“витримує” множення на всі елементи кільця  ).
).
u Ідеал 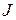 кільця
кільця  називається головним, якщо існує елемент
називається головним, якщо існує елемент  такий, що
такий, що 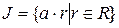 , тобто
, тобто 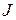 складається з елементів, кратних
складається з елементів, кратних 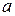 . Кажуть, що головний ідеал
. Кажуть, що головний ідеал 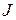 породжується елементом
породжується елементом 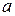 і позначають
і позначають  .
.
u Цілісне кільце, в якому кожен ідеал є гловним, називається кільцем головних ідеалів.
Наприклад, кільце цілих чисел є кільцем головних ідеалів. Кожен ідеал 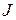 у ньому складається з чисел, кратних деякому цілому числу
у ньому складається з чисел, кратних деякому цілому числу 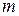 , тобто
, тобто 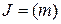 . Так, парні числа утворюють ідеал (2).
. Так, парні числа утворюють ідеал (2).
Кожен ідеал 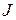 кільця
кільця  визначає розбиття
визначає розбиття  на класи лишків за модулем ідеалу
на класи лишків за модулем ідеалу 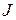 . Клас лишків, що містить елемент
. Клас лишків, що містить елемент 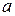 , позначатимемо
, позначатимемо 
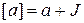 ; він складається з усіх елементів виду
; він складається з усіх елементів виду 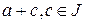 . Два елементи
. Два елементи 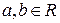 належать одному класу лишків тоді і тільки тоді, коли
належать одному класу лишків тоді і тільки тоді, коли 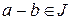 .
.
Множина класів лишків кільця  за модулем ідеалу
за модулем ідеалу 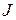 утворює кільце відносно операцій додавання та множення, що визначені наступним чином:
утворює кільце відносно операцій додавання та множення, що визначені наступним чином:
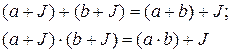
або, що те саме,

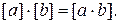
uКільце класів лишків кільця  за модулем ідеалу
за модулем ідеалу 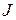 з операціями, визначеними вище, називається фактор-кільцем кільця
з операціями, визначеними вище, називається фактор-кільцем кільця  за ідеалом
за ідеалом 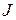 і позначається
і позначається 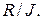
u Оборотним елементом кільця  називається такий елемент
називається такий елемент 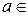
 , для якого виконується умова
, для якого виконується умова 
 ):
): 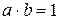 . Елемент
. Елемент 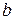 називається оберненим до
називається оберненим до 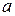 і позначається
і позначається 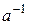 .
.
Нуль кільця є необоротним елементом.
Поняття гомоморфізму природним чином поширюється і на кільця.
u Відображення 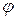 кільця
кільця  у кільце
у кільце 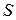 називається гоморфізмом, якщо
називається гоморфізмом, якщо 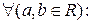
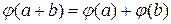 та
та 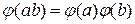 .
.
Таким чином, гомоморфізм 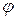 зберігає обидві операції кільця
зберігає обидві операції кільця  та індукує гомоморфізм адитивної групи кільця
та індукує гомоморфізм адитивної групи кільця  в адитивну групу кільця
в адитивну групу кільця 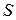 .
.
Так само поширюються на кільця поняття епі-, ендо-, ізо- та автоморфізмів.
u Множина 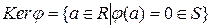 називається ядром гомоморфізму
називається ядром гомоморфізму 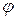 .
.
ТЕОРЕМА (про гоморфізм кілець)* ) Якщо 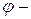 гоморфізм кільця
гоморфізм кільця  на кільце
на кільце 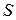 , то
, то 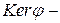 ідеал кільця
ідеал кільця  і
і 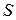 ізоморфне фактор-кільцю
ізоморфне фактор-кільцю 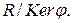 Навпаки, якщо
Навпаки, якщо 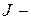 ідеал кільця
ідеал кільця  , то відображення
, то відображення 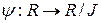 , що визначається умовою
, що визначається умовою  :
: 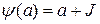 , є гомоморфізмом кільця
, є гомоморфізмом кільця  на
на  з ядром
з ядром 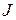 .
.
u Полем 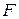 називається алгебраїчна структура з двома операціями: додаванням і множенням, що задовольняють умовам:
називається алгебраїчна структура з двома операціями: додаванням і множенням, що задовольняють умовам:
1) за додаванням 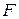 є абелевою групою;
є абелевою групою;
2) за множенням усі ненульові елементи 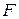 також утворюють абелеву групу;
також утворюють абелеву групу;
3) додавання і множення пов'язані законом дистрибутивності:
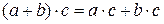 .
.
З означення поля видно, що на відміну від комутативного кільця з одиницею, у полі кожен ненульовий елемент є оборотним.
› Надалі приймемо позначення: N – множина натуральних чисел, Z – кільце цілих чисел, Q – поле раціональних чисел, R – поле дійсних чисел, C – поле комплексних чисел.
_____________________
*) Ця теорема, а також поняття ядра гомоморфізму та фактор-кільця є узагальненням відповідних понять та теореми теорії груп.
Контрольні питання до §1
1. Дати визначення групи, кільця, поля та навести приклади цих алгебраїчних структур.
2. Сформулювати теорему Лагранжа.
3. Дати визначення порядку елемента групи.
4. Дати визначення гомоморфізму груп та кілець.
5. Сформулювати теорему про гомоморфізм кілець.
Date: 2015-09-18; view: 676; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |