Примеры решения задач. 3.2.1.Решить линейную систему

3.2.1. Решить линейную систему

(3.6)

Решение 1 (По формулам Крамера).

◄ Линейная система (3.6) – квадратная: число уравнений равно числу неизвестных – трем. Определитель основной матрицы (из коэффициентов при неизвестных)

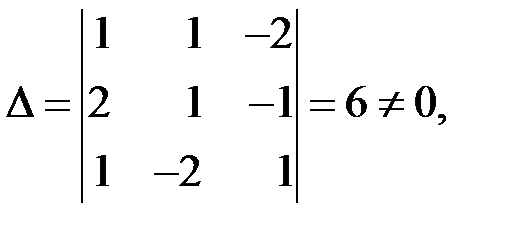
то есть система невырожденная, и можно применять формулы Крамера (3.3). Составим и вычислим определители 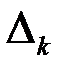, , 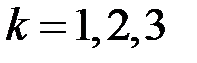заменив в 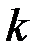-й столбец на столбец свободных членов:

, , .

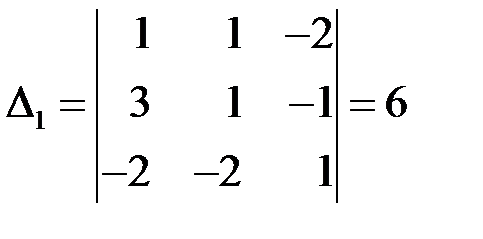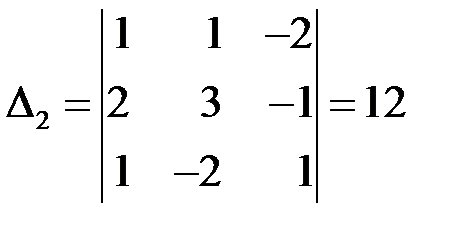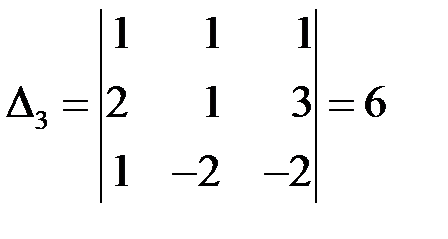По формулам Крамера (3.3) , , .►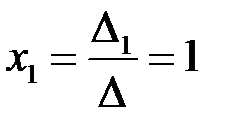

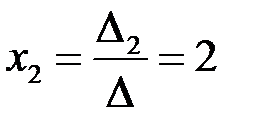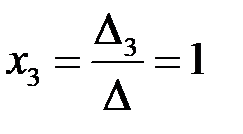Решение 2 (Матричным методом – с помощью обратной матрицы).

◄ Линейную систему (3.6) можно записать в виде одного матричного уравнения 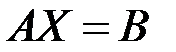, где 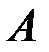– основная матрица системы, 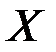– матрица-столбец из неизвестных 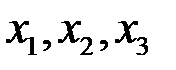, 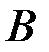– матрица-столбец из свободных членов. Матрица, обратная к 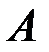, была вычислена в примере 2.2.5. Решение системы находим по формуле (3.2):

,

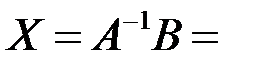
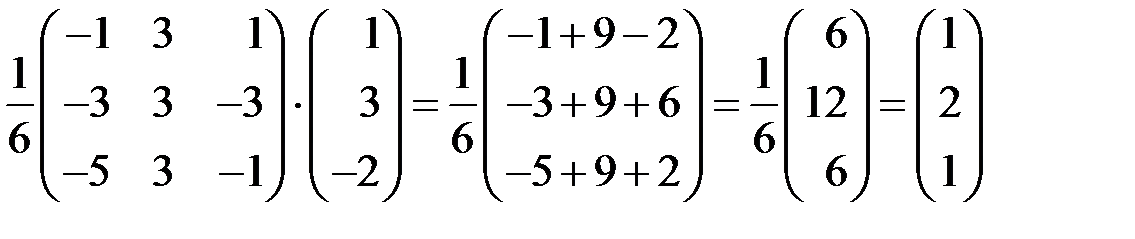то есть .►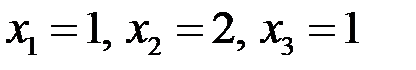

Решение 3 (Методом Гаусса).

◄ Прямой ход метода:

Шаг 1. Ко второму уравнению прибавляем первое, умноженное на (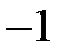), к третьему прибавляем первое, умноженное на ().

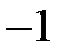Шаг 2. К третьему уравнению прибавляем первое, умноженное на ().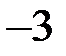

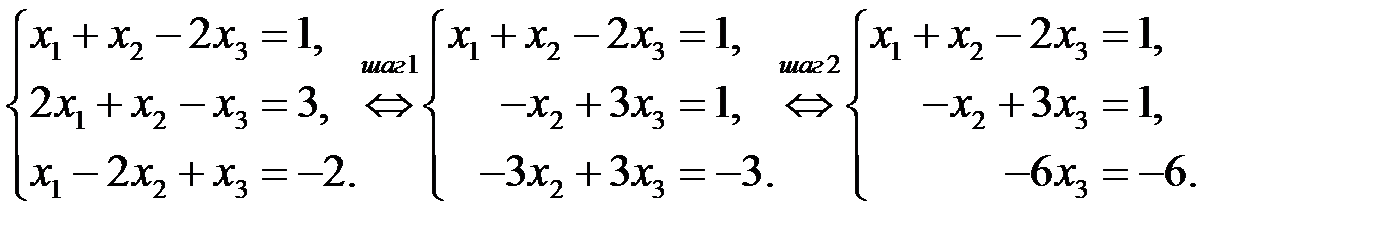
Обратный ход метода: Начиная с последнего уравнения, последовательно находим :

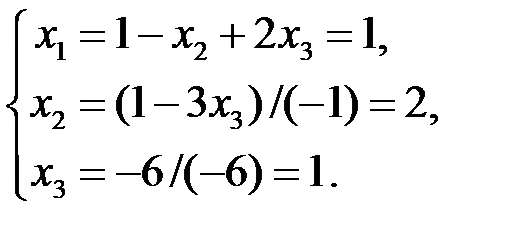
Замечание. Разумно упростить процедуру, выписывая только матрицу из коэффициентов при неизвестных и свободных членов (расширенную матрицу системы):

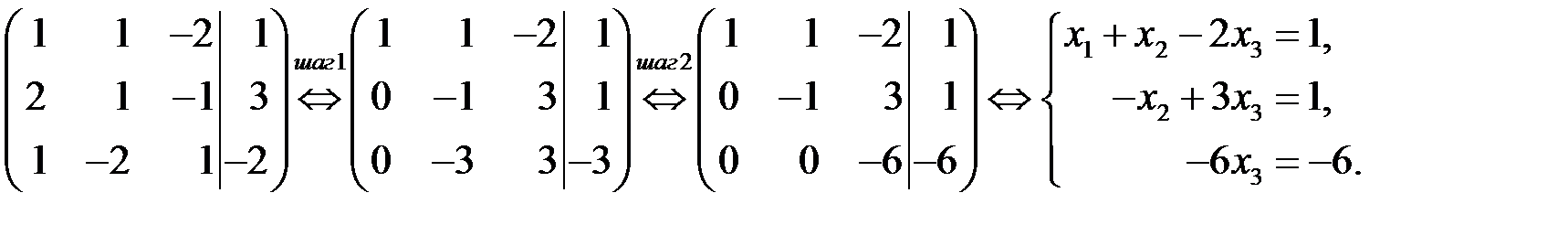
На последнем шаге прямого хода мы для наглядности все-таки вернулись к подробной записи системы. ►

3.2.2. Решить линейную систему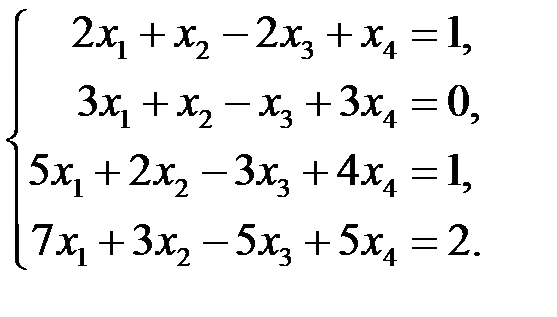

◄ Решаем методом Гаусса. Прямой ход метода:

Шаг 1. Первое уравнение заменим на разность между вторым и первым. Цель – получить 1 в качестве коэффициента при 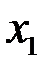в первом уравнении.

Шаг 2. Ко второму уравнению прибавляем первое, умноженное на (–3), к третьему прибавляем первое, умноженное на (–5), к четвертому прибавляем первое, умноженное на (–7).

Шаг 3. К третьему уравнению прибавляем второе, умноженное на (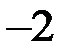), к четвертому прибавляем второе, умноженное на (–3).

Шаг 4. Отбрасываем нулевые уравнения.

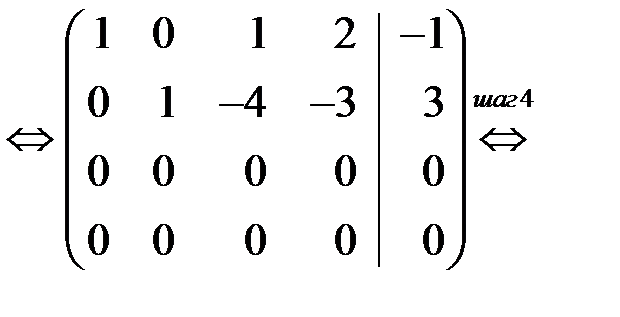
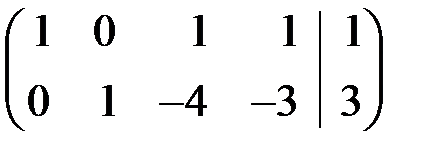
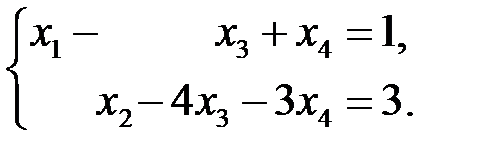
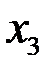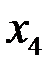Обратный ход метода: Неизвестным и можно придать произвольные значения: 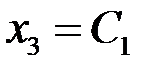, 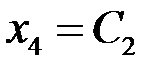. Тогда

, .

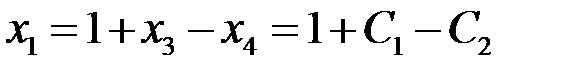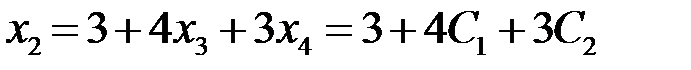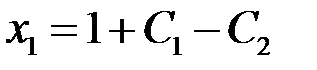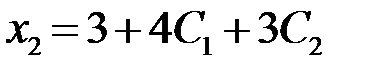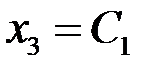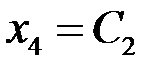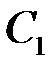Таким образом, все решения (общее решение) системы задаются формулами , , , , где и 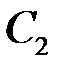– произвольные числа. Меняя 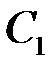и 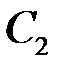, мы получим любое решение. ►

Date: 2015-09-18; view: 406; Нарушение авторских прав