
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Граф электрической цепи
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Рассмотрим соотношения в электрической цепи, обусловленные способом соединения элементов.
Пусть цепь состоит из двухполюсников. В простейшем случае эти элементы могут быть соединены последовательно или параллельно.
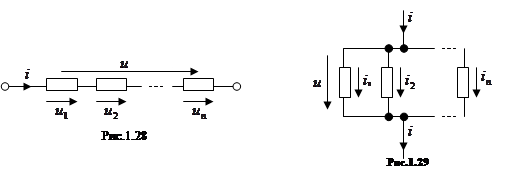
При последовательном соединении любые два соседних элемента имеют общий зажим (рис. 1.28), токи во всех элементах одинаковы. Напряжение на зажимах всего соединения равно сумме напряжений отдельных элементов
 |
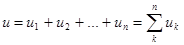 . (1.13)
. (1.13)
При параллельном соединении все элементы присоединяются к одной и той же паре узлов, так что напряжения на всех элементах одинаковы (рис. 1.29). Ток в неразветвленной части цепи равен сумме токов всех элементов
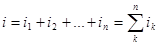 . (1.14)
. (1.14)
Соотношения (1.13) и (1.14) справедливы для соединений любых элементов (резистивных, индуктивных и т. д.). Их вид определяются только способом соединения элементов, или, как говорят, геометрией (топологией) соединений.
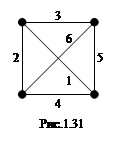 |
 Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому каждую ветвь можно изобразить отрезком прямой. На рис. 1.31 показан граф электрической цепи, изображенной на рис. 1.30.
Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому каждую ветвь можно изобразить отрезком прямой. На рис. 1.31 показан граф электрической цепи, изображенной на рис. 1.30.
 |
На графе источники ЭДС и тока не изображаются. При этом ветвь с источником ЭДС сохраняется, ветвь с источником тока не показывается. Отрезки прямых называются ветвями графа, концевые точки ветви графа – узлами графа.
Ветвям графа может быть дана определенная ориентация, указанная стрелками. Граф, у которого все ветви ориентированы, называется ориентированным. В противном случае - неориентированным.
Подграфом графа называется часть графа (одна ветвь, один узел, любое множество ветвей и узлов графа). В теории цепей различают подграфы: путь, контур, дерево, связи и сечение.
Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел в этом пути встречается один раз. На рис. 1.31 имеем пути: 3-4-5; 2-1-5 и т.д.
Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. На рис. 1.31 имеем контуры: 2-3-6, 2-3-5-4 и т.д.
Если между любой парой узлов графа (схемы) существует путь, то такой граф (схема) называется связным.
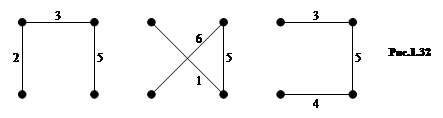
Деревом связного графа (схемы) называют связной подграф (подсхему), содержащий все узлы графа (схемы), но ни одного контура. Деревья графа рис. (1.31) показаны на рис. 1.32.
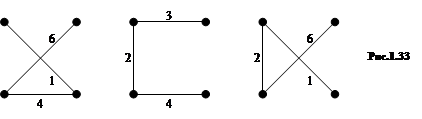
Ветви графа (схемы), которые дополняют дерево до исходного графа, называются ветвями связи (дополнениями дерева). Ветви связи деревьев рис. 1.32 показаны на рис. 1.33.
 |
Если граф (схема) содержит «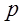 » ветвей и «
» ветвей и «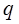 » узлов, то число ветвей любого дерева
» узлов, то число ветвей любого дерева 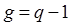 . Число ветвей связи графа
. Число ветвей связи графа 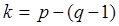 .
.
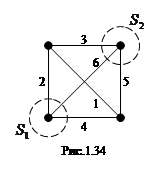 Сечением графа (схемы) называется множество ветвей, удаление которых делит граф (схему) на два изолированных подграфа (подсхемы), один из которых в частном случае может быть изолированным узлом. Сечение можно изобразить в виде следа замкнутой поверхности, рассекающей соответствующие ветви. Такие поверхности (
Сечением графа (схемы) называется множество ветвей, удаление которых делит граф (схему) на два изолированных подграфа (подсхемы), один из которых в частном случае может быть изолированным узлом. Сечение можно изобразить в виде следа замкнутой поверхности, рассекающей соответствующие ветви. Такие поверхности (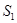 ;
; 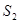 ) показаны на рис. 1.34.
) показаны на рис. 1.34.
 Главным контуром называется контур, состоящий из ветвей дерева и только одной ветви связи. Число главных контуров
Главным контуром называется контур, состоящий из ветвей дерева и только одной ветви связи. Число главных контуров 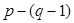 .
.
Главным сечением называется сечение, состоящее из ветвей связи и одной ветви дерева. Каждая ветвь дерева позволяет образовать одно главное сечение. Число главных сечений 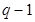 .
.
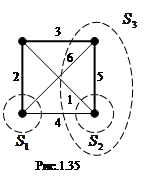
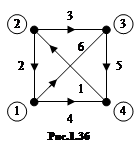
На рис. 1.35 жирными линиями показано дерево. Главные контуры: 2-3-6; 3-5-1; 2-3-5-4. Главные сечения: изображены поверхностями 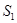 ;
; 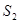 и
и 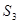 .
.
Вопрос о числе независимых уравнений, которые можно составить по законам Кирхгофа, можно решить, применяя понятие дерева графа (схемы). Можно показать, что:
· уравнения по I закону Кирхгофа, составленные для главных сечений – независимы;
· уравнения по II закону Кирхгофа для главных контуров – независимы.
По I закону Кирхгофа составляют 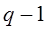 независимых уравнений. По II закону Кирхгофа составляют
независимых уравнений. По II закону Кирхгофа составляют 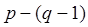 независимых уравнений.
независимых уравнений.
 1.7. Топологические матрицы графа.
1.7. Топологические матрицы графа.
Рассмотрим ориентированный граф (рис. 1.36), соответствующий схеме (рис. 1.30). Составим независимые уравнения Кирхгофа для узлов 1, 2, 3
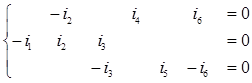 .
.


 |
|
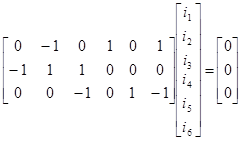 .
.
Элементы топологической матрицы равны +1, -1, 0. Значения этих элементов определяются только структурой графа (схемы).
В соответствии с видом уравнений Кирхгофа различают три топологические матрицы: матрицу соединений (узловую матрицу) 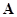 , матрицу сечений
, матрицу сечений 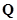 и матрицу контуров
и матрицу контуров 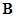 .
.
Матрица соединений (узловая матрица) 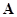 - это таблица коэффициентов уравнений, составленных по I закону Кирхгофа для узлов.
- это таблица коэффициентов уравнений, составленных по I закону Кирхгофа для узлов.
Строки матрицы соответствуют узлам (число строк равно числу независимых узлов, т.е. 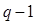 ), столбцы – ветвям. Если записать
), столбцы – ветвям. Если записать 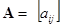 ,
, 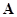 - узловая матрица (
- узловая матрица (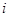 - номер строки,
- номер строки, 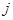 - номер столбца).
- номер столбца).
Правило составления 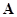 :
: 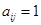 , если ветвь
, если ветвь 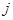 соединена с узлом
соединена с узлом 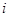 и направлена от узла
и направлена от узла 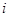 ;
; 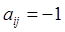 , если ветвь
, если ветвь 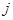 соединена с узлом
соединена с узлом 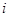 и направлена к узлу
и направлена к узлу 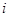 ,
, 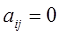 , если ветвь
, если ветвь 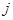 не соединена с узлом
не соединена с узлом 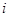 .
.
Если обозначить
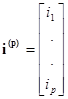 ,
,
то матричная форма уравнений по I закону Кирхгофа для узлов будет
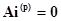 . (1.15)
. (1.15)
С помощью матрицы 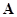 можно выразить напряжения ветвей (
можно выразить напряжения ветвей (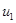 ,
, 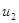 , …,
, …, 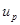 ) через потенциалы узлов (
) через потенциалы узлов (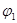 ,
, 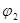 , …,
, …, 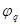 )
)
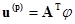 , (1.16)
, (1.16)
где 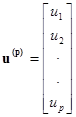 ,
, 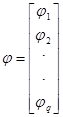 ,
, 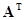 - транспонированная узловая матрица.
- транспонированная узловая матрица.
Матрица сечений 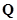 - это таблица коэффициентов уравнений, составленных по I закону Кирхгофа для сечений. Строки матрицы соответствуют сечениям, столбцы ветвям.
- это таблица коэффициентов уравнений, составленных по I закону Кирхгофа для сечений. Строки матрицы соответствуют сечениям, столбцы ветвям.
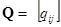 .
.
 , если ветвь
, если ветвь 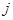 содержится в сечении
содержится в сечении 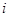 и направлена согласно с направлением сечения (ток ветви дерева
и направлена согласно с направлением сечения (ток ветви дерева 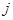 направлен наружу замкнутой поверхности).
направлен наружу замкнутой поверхности).  , если ветвь
, если ветвь 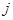 содержится в сечении
содержится в сечении 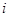 и направлена противоположно направлению сечения;
и направлена противоположно направлению сечения; 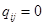 , если ветвь
, если ветвь 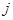 не содержится в сечении
не содержится в сечении 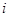 . Число строк матрицы
. Число строк матрицы 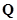 равно
равно 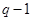 - числу независимых контуров.
- числу независимых контуров.
Если матрица 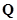 составлена для главных сечений, то ее называют матрицей главных сечений. При этом за положительное направление сечения берут направление ветви дерева данного сечения (рис. 1.37)
составлена для главных сечений, то ее называют матрицей главных сечений. При этом за положительное направление сечения берут направление ветви дерева данного сечения (рис. 1.37)
|
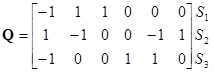 ,
,
где 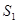 ,
, 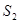 ,
, 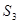 - независимые сечения
- независимые сечения
Закон Кирхгофа для сечений в матричной форме:
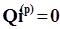 . (1.17)
. (1.17)
Если матрицу напряжений ветвей дерева обозначить через 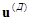 , то
, то
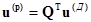 . (1.18)
. (1.18)
Матрица контуров 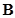 - это таблица коэффициентов уравнений, составленных по II закону Кирхгофа. Строки матрицы соответствуют контурам, столбцы – ветвям.
- это таблица коэффициентов уравнений, составленных по II закону Кирхгофа. Строки матрицы соответствуют контурам, столбцы – ветвям.
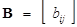 .
.
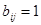 , если ветвь
, если ветвь 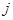 содержится в контуре
содержится в контуре 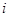 и направление ветви совпадает с направлением обхода контура;
и направление ветви совпадает с направлением обхода контура; 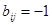 , если ветвь
, если ветвь 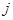 содержится в контуре
содержится в контуре 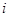 и ее направление против обхода контура;
и ее направление против обхода контура; 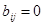 , если ветвь
, если ветвь 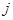 не содержится в контуре
не содержится в контуре 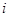 .
.
Матрицу 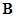 , записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура.
, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура.
Число строк матрицы 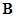 равно числу независимых контуров
равно числу независимых контуров 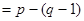 .
.
Второй закон Кирхгофа в матричной форме:
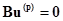 , (1.19)
, (1.19)
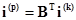 , (1.20)
, (1.20)
где 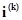 - матрица-столбец контурных токов.
- матрица-столбец контурных токов.
Матрицы 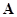 ,
, 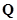 ,
, 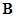 позволяют выразить алгебраическим языком топологию схем, что важно при анализе сложных цепей с помощью компьютера.
позволяют выразить алгебраическим языком топологию схем, что важно при анализе сложных цепей с помощью компьютера.
Соотношения между топологическими матрицами. Если матрицы 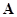 ,
, 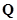 ,
, 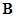 составлены для одного и того же графа (схемы), то имеет место:
составлены для одного и того же графа (схемы), то имеет место:
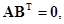 , (1.21)
, (1.21)
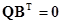 . (1.22)
. (1.22)
Date: 2015-09-17; view: 3467; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |