Представление числовой информации в ЭВМ

В вопросах организации обработки информации с помощью ЭВМ важное место занимают системы счисления, формы представления данных и специальное кодирование чисел.

Системы счисления. Под системой счисления понимается способ представления любого числа с помощью ограниченного набора символов, называемых цифрами.

Различают позиционные и непозиционные системы счисления. В позиционных системах количественное значение каждой цифры зависит от ее места (позиции) в числе. В непозиционных системах цифра не меняет своего количественного значения при изменении позиции. Пример непозиционной системы – Римские цифры.

Количество q различных цифр, используемых для изображения чисел в позиционной системе, называется основанием системы счисления. В общем случае в позиционной системе счисления с основанием q любое число Х может быть представлено в виде полинома:

Х_(q) = x_n–1q^n–1+x_n–2q^n–2+…+ x₁q¹+x₀q⁰+x_–1q^–1+…+x_–mq^–m = 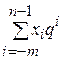, (2.1)

где Х_(q) - запись числа в системе счисления с основанием q;

x_i - целые числа, меньше q;

n - число разрядов (позиции) в целой части числа;

m - число разрядов в дробной части числа.

Например:

4295, 6731₍₁₀₎ = 4· 10³+2·10²+ 9·10¹+5·10⁰+6·10^–1+7·10^–2+3×10^–3+1·10^–4.

В информатике применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную и шестнадцатеричную, т. е. системы счисления с основанием q = 2^k, где k =1, 3, 4. Наибольшее распространение получила двоичная система счисления с q = 2. В этой системе для представления любого числа используются два символа – цифры 0 и 1. Произвольное число с помощью формулы (2.1) можно представить в виде разложения по степеням двойки:

X₍₂₎ = x_n–12^n–1+x_n–22^n–2+…+x₁2¹+…+x_–m2^–m.

Например:

13,625₍₁₀₎ = 1·2³ + 1·2² +0·2¹ + 1·2⁰+1·2^–1 + 0·2^–2 + 1·2^–3 = 1101,101₍₂₎.

Двоичное представление числа требует примерно в 3,3 раза большего числа разрядов, чем его десятичное представление. Тем не менее, применение двоичной системы счисления создает большие удобства для работы ЭВМ, т. к. для представления в машине разряда двоичного числа может быть использован любой запоминающий элемент, имеющий два устойчивых состояния. Таких технических устройств достаточно много.

Преобразование числа Х из системы счисления с основанием р в систему счисления с основанием q (преобразование X_(р) → Х_(q)) осуществляется по правилу замещения, т.е. по формуле (2.1).

В ЭВМ применяются следующие формы представления числовых данных:

• числа с фиксированной точкой (запятой);

• числа с плавающей точкой (запятой);

Представление числа Х в форме с фиксированной точкой называют естественной формой. Место точки (запятой) постоянно для всех чисел и в процессе решения задач не меняется. Знак положительного числа кодируется цифрой "0", а знак отрицательного числа – цифрой "1".

Форма представления чисел с фиксированной точкой упрощает аппаратную реализацию ЭВМ, уменьшает время выполнения, машинных операций, однако при решении задач на машине необходимо постоянно следить за тем, чтобы все исходные данные, промежуточные и окончательные результаты находились в допустимом диапазоне представления. Если этого не соблюдать, то возможно переполнение разрядной сетки, и результат вычислений будет неверным.

От этих недостатков в значительной степени свободны ЭВМ, использующие форму представления чисел с плавающей точкой, или нормальную форму, в которой число представляется в виде произведения

Х = m×q^k,

где m - мантисса числа; q -основание системы счисления (характеристика числа); k - порядок.

Для кодирования целых чисел от 0 до 255 достаточно иметь 8 разрядов двоичного кода (8 бит). Шестнадцать бит позволяют закодировать целые числа от 0 до 65535, а 24 бита – уже более 16,6 миллионов разных значений.

Чтобы кодировать действительные числа используют 80- разрядное кодирование. При этом число предварительно преобразуется в нормализованную форму, например:

3,1415926 = 0,31415926×10¹;

300 000 = 0,3×10⁶;

123 456 789 = 0,123456789×10¹⁰.

Большую часть из 80 бит отводят для хранения мантиссы (вместе со знаком) и некоторое фиксированное количество разрядов отводят для хранения порядка (тоже со знаком).

Арифметические операции в позиционных системах счисления выполняются по одним и тем же правилам для всех систем. Рассмотрим сложение целых чисел с фиксированной точкой в двоичной системе. В его основе лежит таблица сложения одноразрядных двоичных чисел:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 10

Обратите внимание, что при сложении двух единиц происходит перенос единицы в старший разряд (также как и в десятичной системе, например, при сложении 8 и 5).

Сложение многоразрядных двоичных чисел происходит в соответствии с вышеприведенной таблицей с учетом возможных переносов из младших разрядов в старшие. Например, сложим 101₍₂₎ и 110₍₂₎:

Проверим правильность результата выполнением сложения в десятичной системе счисления. Переведем оба слагаемых в десятичную систему и сложим их.

101₍₂₎ = 1×2² + 1×2⁰ = 5₍₁₀₎ ;

110₍₂₎ = 1×2² + 1×2¹ = 6₍₁₀₎ ;

5+6 = 11;

1011₍₂₎ = 1×2³ +1×2¹ +1×2⁰ = 8₍₁₀₎ + 2₍₁₀₎ + 1₍₁₀₎ = 11₍₁₀₎.

Сложение выполнено правильно.

При сложении и вычитании нормализованных чисел (с плавающей точкой) сначала производится подготовительная операция, называемая выравниванием порядков. В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.

В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются.

В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.

Пример. Сложить двоичные нормализованные числа 0.10111×10^–1 и 0.11011×10¹⁰.

Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо:

Date: 2015-09-05; view: 626; Нарушение авторских прав