Проблемы численных методов и выбор метода решения д.у

Выбрать метод решения Д.У. можно в меню модели Simulink Simulation команда Simulation Parameters.

Параметр Solver Options (Параметры решателя).

Там выбирается тип решателя:

Variable-step (с переменным шагом) – шаг подбирается автоматически для достижения заданной точности.

Fixed-step (с постоянным шагом)

Методы решения с постоянным шагом:

ode5 – метод Рунге-Кутты 5 порядка точности;

ode4 – метод Рунге-Кутты 4 порядка точности;

…

ode1 – метод Эйлера.

Эти методы используются, если заранее известны свойства решения и можно заранее подобрать шаг интегрирования. Тогда решение выполняется быстро.

Методы решения с переменным шагом:

ode45 – метод Рунге-Кутты 4-5 порядка точности – наиболее часто используемый решатель.

ode23 – метод Рунге-Кутты 2-3 порядка точности. Для обеспечения такой же точности как ode45 приходится использовать меньший шаг.

Одна из основных проблем, возникающих при решении дифференциальных уравнений – это проблема устойчивости.

Пример. Рассмотрим дифференциальное уравнение:

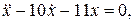
с начальными условиями: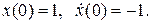

Решение этой задачи: 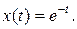Теперь изменим первое начальное условие на малую величину ε: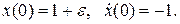

Решением этой задачи будет:

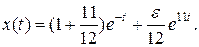
Таким образом, при сколь угодно малом ε>0, второй член в решении приводит к тому, что решение стремится к бесконечности при t→∞, т.е. становится неустойчивым.

Задачи, у которых сколь угодно малые изменения начальных условий могут привести к сколь угодно большим изменениям решения при t→∞, в численном анализе называют плохо обусловленными.

Для таких задач очень трудно получить решение, так как машинные погрешности приводят к тому, что решение уходит в бесконечность.

Мы рассмотрели неустойчивость самих решений дифференциальных уравнений. Неустойчивым может быть и численный метод решения дифференциального уравнения – устойчивость разностного уравнения.

При численном решении дифференциальных уравнений метод может быть устойчивым при маленьких шагах интегрирования, но терять устойчивость при больших шагах.

Использование малых шагов интегрирования может привести к очень большим потерям времени. Такие ситуации часто возникают при решении жестких уравнений.

Пример жесткого уравнения.

Рассмотрим линейное дифференциальное уравнение второго порядка:

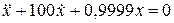
Начальные условия: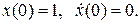

Решение – x (t) = –0,0001 e ^{–99,99 t} + 1,0001 e ^{–0,01 t}

Первая составляющая имеет начальное значение – 0,0001 и быстро затухает;

Второй компонент имеет начальной значение в 10 000 раз больше и убывает в 10 000 раз медленнее.

В начале решение нужно проводить с очень маленьким шагом интегрирования. Первая составляющая очень быстро затухает, но ее по-прежнему нужно учитывать: если увеличить шаг интегрирования, то решение станет неустойчивым.

Жесткие системы характеризуются разномасштабностью процессов, описываемых данной системой. Быстроубывающий компонент, который обычно не представляет интереса, отрицательно влияет на устойчивость.

Если использовать обычные методы для решения жестких систем шаг нужно выбирать очень маленьким.

Для решения жестких систем нужно использовать специальные методы.

Есть специальная группа методов для решения жестких систем дифференциальных уравнений (Stiff).

Это функции:

ode15s – неявный многошаговый разностный метод. Для нежестких задач эта функция неэффективна.

ode23s – модифицированный метод Розенброка. Используется для умеренно жестких задач с низкими требованиями по точности. Скорость решения больше, чем у ode15s.