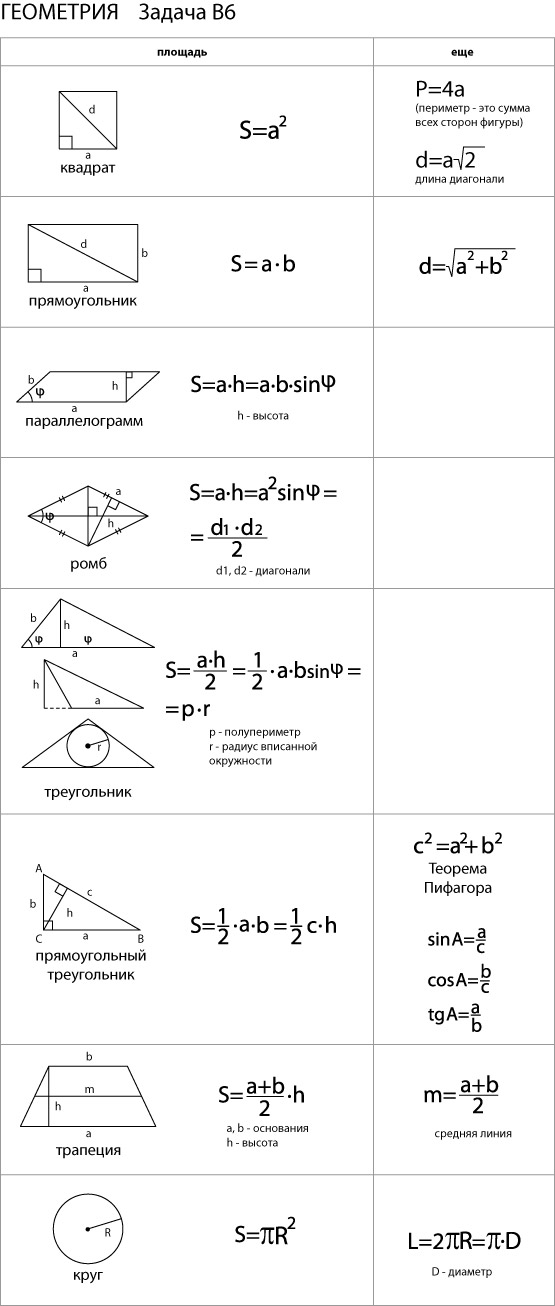
Площадь

Здесь приведены формулы, свойственные именно трапеции.

В случае, есл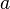и и 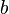— основания и 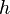— высота, формула площади:

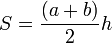
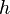В случае, если — средняя линия и — высота, формула площади:

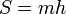
ɴʙ Приведенные выше две формулы эквивалентны, так как полусумма оснований равняется средней линии трапеции:

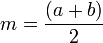
Формула, где 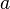, 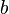— основания, и 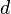— боковые стороны трапеции:

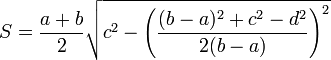
Площадь равнобедренной трапеции с радиусом вписанной окружности, равным , и углом при основании :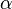

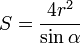
В частности, если угол при основании равен 30°, то:

.

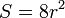Свойства равнобедренной трапеции
1). Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции.
2). Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
3). В равнобедренной трапеции углы при любом основании равны.
4). В равнобедренной трапеции длины диагоналей равны.
5). Если в трапецию можно вписать окружность, то она равнобедренная.
6). Около равнобедренной трапеции можно описать окружность.
7). Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Date: 2015-09-05; view: 2484; Нарушение авторских прав