Определение уклонений отвеса

Отвесная линия (вертикаль) совпадает с направление вектора силы тяжести g.

Она является нормалью к уровенной поверхности. С другой стороны нормаль к эллипсоиду совпадает с направлением вектора нормальной силы тяжести. Эти две нормали не совпадают. Между ними образуется угол, который геодезисты называют уклонением отвеса. Не будет ошибкой сказать и отклонение отвесной линии. Правда возникает вопрос отклонение от чего? Чтобы таких вопросов не возникало, мы будем употреблять геодезический термин.

Две упомянутые нормали, продолженные вверх, пересекаются с воображаемой небесной сферой в точках, одна из которых будет астрономическим зенитом (или просто зенитом), а другая -- геодезическим. Понятно, что и плоскости горизонта астрономического и геодезического не совпадают. Договорились считать уклонения отвеса положительным, если зенит смещается в северном или восточном направлении.

Обратимся к локальной геодезической системе координат с началом в пункте наблюдений (точка ). Горизонтальные оси PX и PY, как мы знаем из лекции 7, лежат в плоскости, перпендикулярной к нормали к эллипсоиду. Одна из них направлена на север, другая -- на восток. Ось PZ направлена вниз по внутренней нормали к эллипсоиду. Нетрудно понять, что при положительных "горизонтальных" компонентах вектора силы тяжести обе компоненты уклонения отвеса будут отрицательны. Поэтому компоненты уклонения отвеса в плоскости меридиана и первого вертикала соответственно определяют следующим образом

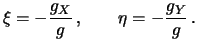
(8.20)

Из приведенных формул видно, что обе компоненты -- безразмерные величины, хотя на практике они измеряются в угловых единицах. Дело в том, что уклонения отвеса на Земле составляют секунды дуги, поэтому вместо тригонометрических формул, связывающих уклонения отвеса с компонентами вектора силы тяжести, мы взяли простое отношение.

С другой стороны

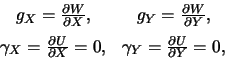
поэтому

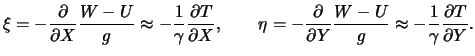
(8.21)

Ранее мы видели, что 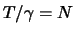, поэтому

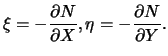
(8.22)

Формула (8.19) позволяет вычислить высоты геоида, если на поверхности Земли заданы смешанные гравитационные аномалии. Принципиально не имеет значения, в каких координатах заданы эти аномалии и в каких координатах практически ведется интегрирование. Мы для этих целей будем применять геодезические координаты 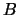и 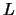. Перепишем формулу (8.19)

Интегрирование будем выполнять на сфере, а не на эллипсоиде. При этом можно ожидать погрешность в определении высот геоида порядка сжатия. Пренебрегая этими погрешностями, определим элементарные приращения для осей PX и PY

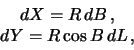
поэтому

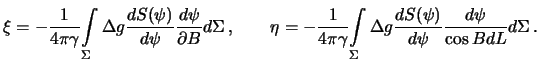
(8.23)

Теперь нужно вычислить производные 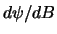и . Для этого обратимся к формулам сферической тригонометрии.

Рассмотрим сферический треугольник, который образуют дуги, соединяющие три точки на сфере: точку , в которой мы хотим определить уклонение отвеса, точку 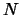-- полюс, и точку 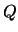-- текущую точку на поверхности сферы, где расположен элемент поверхности. Дуга PN равна 90- 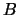, а дуга QN равна 90- 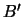. Угол при точке равен 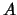-- азимуту текущей точки 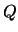Дуга РР' равна аргументу функции Стокса -- 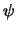. Угол при полюсе 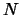равен разности долгот точки 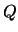и точки , то есть . 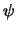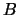Используя формулы сферической тригонометрии, несложно получить производные угла по и по 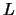, входящие в формулы (8.23)

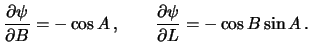
Подставим полученные выражения в (8.23), получим

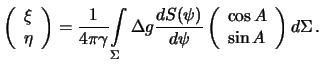
Запишем приведенный интеграл в виде двукратного интеграла. Элемент сферы равен 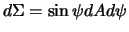, причем переменная 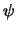изменяется от 0 до 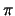, а переменная 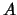-- от 0 до 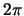. Получим

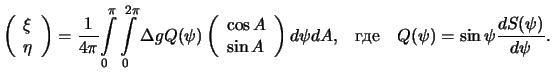
(8.24)

Эти формулы носят имя голландского ученого Венинг-Мейнеса. Как и в формулу Стокса, определяющей высоту геоида точка 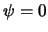является устранимой особой точкой.

На практике используют более сложные методики для вычисления уклонений отвеса с использованием и гравиметрических и геодезических данных.

<< Лекция 7. Нормальное поле тяжести | Оглавление | Лекция 9. Квазигеоид Молоденского >>

<< Лекция 8. Определение фигуры геоида | Оглавление |

Date: 2015-09-05; view: 987; Нарушение авторских прав