
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методы анализа сетей Петри
Лекция 4.
Поведенческие свойства сетей Петри.
Пример сети Петри и её графа.
C = (P, T, I, O), P = { p 1, p 2 p 3, p 4, p 5}, T = { t 1, t 2 t 3, t 4}
I (t 1) = { p 1}, O (t 1) = { p 2, p 3, р 5},
I (t 2) = { p 2, p 3, p 5}, O (t 2) = { p 5},
I (t 3) = { p 3}, O (t 3) = { р 4},
I (t 4) = { p 4}, O (t 4) = { p 2, p 3}.
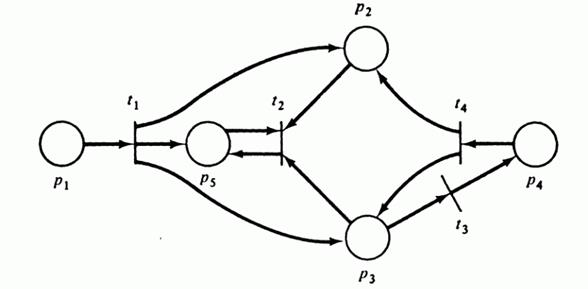
Рис 4.1: Пример сети Петри.
Привести пример какой-нибудь маркировки.
Функция следующего состояния.
Состояние, сети Петри определяется ее маркировкой. Запуск перехода изменяет состояние сети. Пространство состояний сети Петри, обладающей n позициями, есть множество всех маркировок, т. е. Nn. Изменение в состоянии, вызванное запуском перехода, определяется функцией изменения d, которую мы назовем функцией следующего состояния: 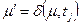 ,
,
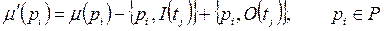 . (4.1)
. (4.1)
Достижимость.
Пусть некоторый переход в маркировке m разрешен и, следовательно, может быть запущен. Результат запуска перехода есть новая маркировка m '. Говорят, что m ' является непосредственно достижимой из маркировки m. если существует переход 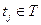 , такой, что
, такой, что 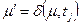 . Если m ' непосредственно достижима из m, a m " — из m ', говорят, что m " достижима из m. Можно записать
. Если m ' непосредственно достижима из m, a m " — из m ', говорят, что m " достижима из m. Можно записать  , где σ — последовательность переходов. Определим множество достижимости R (C, m) сети Петри С с маркировкой m как множество всех маркировок, достижимых из m. Маркировка m ' принадлежит R (C, m), если существует какая-либо последовательность запусков переходов, изменяющих m на m '.
, где σ — последовательность переходов. Определим множество достижимости R (C, m) сети Петри С с маркировкой m как множество всех маркировок, достижимых из m. Маркировка m ' принадлежит R (C, m), если существует какая-либо последовательность запусков переходов, изменяющих m на m '.
Безопасность.
Одно из важнейших свойств сети Петри, которая должна моделировать реальное устройство, — безопасность. Позиция сети Петри является безопасной, если число фишек в ней никогда не превышает 1. Позиция 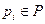 сети Петри C = (P, T, I, O) с начальной маркировкой m является безопасной, если
сети Петри C = (P, T, I, O) с начальной маркировкой m является безопасной, если 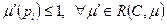 . Сеть Петри безопасна, если безопасны все позиции сети. В первоначальном определении сети Петри были безопасны, поскольку переход не мог быть запущен, если не все из выходных позиций были пусты (а кратные дуги не были разрешены).
. Сеть Петри безопасна, если безопасны все позиции сети. В первоначальном определении сети Петри были безопасны, поскольку переход не мог быть запущен, если не все из выходных позиций были пусты (а кратные дуги не были разрешены).
Если позиция не является кратной входной или кратной выходной для перехода, ее можно сделать безопасной. К позиции 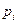 , которую необходимо сделать безопасной, добавляется новая позиция
, которую необходимо сделать безопасной, добавляется новая позиция 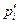 Переходы, в которых
Переходы, в которых 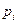 используется в качестве входной или выходной, модифицируются следующим образом:
используется в качестве входной или выходной, модифицируются следующим образом:
Если 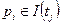 и
и 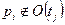 , тогда добавить
, тогда добавить 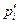 к
к 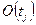
Если 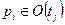 и
и 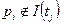 , тогда добавить
, тогда добавить 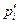 к
к 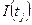 .
.
Цель введения этой новой позиции 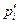 — представить условие «
— представить условие «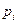 пуста». Следовательно,
пуста». Следовательно, 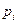 и
и 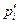 дополнительны;
дополнительны; 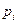 имеет фишку, только если
имеет фишку, только если 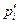 не имеет фишки и наоборот. Любой переход, удаляющий фишку из
не имеет фишки и наоборот. Любой переход, удаляющий фишку из 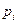 должен помещать фишку в
должен помещать фишку в 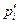 , а всякий переход, удаляющий фишку из
, а всякий переход, удаляющий фишку из 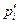 , должен помещать фишку в
, должен помещать фишку в 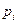 .
.
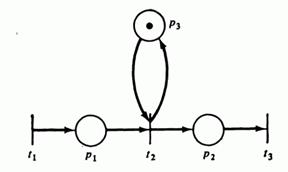
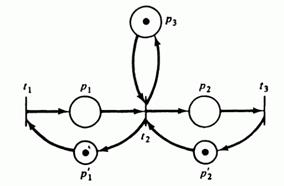
а) б)
Рис 4.2: а) Опасная сеть Петри; б) Эквивалентная ей безопасная сеть Петри.
Безопасность — это частный случай более общего свойства ограниченности. Позиция является k -безопасной или k -ограниченной, если количество фишек в ней не может превышать целое число k. Заметим, что граница по числу фишек, которые могут находиться в позиции, может быть функцией от позиции. Если позиция 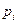 k -безопасна, то она также и k '-безопасна для всех k ' > k. Поскольку число позиций конечно, можно выбрать k, равное максимуму из границ. Сеть Петри называется k -безопасной, если каждая позиция сети k -безопасна. Позиция называется ограниченной, если она k -безопасна для некоторого k, сеть Петри ограниченна, если все ее позиции ограниченны. Ограниченную сеть Петри можно реализовать аппаратно, тогда как сеть Петри с неограниченными позициями в общем случае реализовать аппаратно нельзя.
k -безопасна, то она также и k '-безопасна для всех k ' > k. Поскольку число позиций конечно, можно выбрать k, равное максимуму из границ. Сеть Петри называется k -безопасной, если каждая позиция сети k -безопасна. Позиция называется ограниченной, если она k -безопасна для некоторого k, сеть Петри ограниченна, если все ее позиции ограниченны. Ограниченную сеть Петри можно реализовать аппаратно, тогда как сеть Петри с неограниченными позициями в общем случае реализовать аппаратно нельзя.
Сохранение.
Сеть Петри C = (P, T, I, O) с начальной маркировкой m называется строго сохраняющей, если для всех 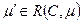 имеет место
имеет место
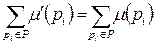 . (4.2)
. (4.2)
Строгое сохранение — это очень сильное ограничение. Например, из него следует, что число входов в каждый переход должно равняться числу выходов.
Сеть Петри C = (P, T, I, O) с начальной маркировкой m называется сохраняющей по отношению к вектору взвешивания w, w = (w 1, w 2,.., wn), n = | P |, wi > 0, если для всех 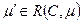
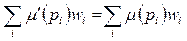 . (4.3)
. (4.3)
Строго сохраняющая сеть Петри является сохраняющей по отношению к вектору взвешивания (1,..., 1).
Активность.
Тупик в сети Петри — это переход (или множество переходов), которые не могут быть запущены. В сети Переход называется активным, если он не заблокирован (нетупиковый). Это не означает, что переход разрешен, скорее он может быть разрешенным. Переход tj сети Петри С называется потенциально допустимым в маркировке m, если существует маркировка 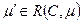 , в которой tj разрешен. Переход активен в маркировке m, если потенциально запустим во всякой маркировке из
, в которой tj разрешен. Переход активен в маркировке m, если потенциально запустим во всякой маркировке из 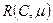 . Следовательно, если переход активен, то всегда возможно перевести сеть Петри из ее текущей маркировки в маркировку, в которой запуск перехода станет разрешенным.
. Следовательно, если переход активен, то всегда возможно перевести сеть Петри из ее текущей маркировки в маркировку, в которой запуск перехода станет разрешенным.
Для заданной маркировки m можно выделить пять уровней активности.
Уровень 0: Переход tj обладает активностью уровня 0, если он никогда не может быть запущен.
Уровень 1: Переход tj обладает активностью уровня 1, если он потенциально запустим, т. е. если существует такая 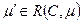 , что tj разрешен в m '.
, что tj разрешен в m '.
Уровень 2: Переход tj; обладает активностью уровня 2, если для всякого целого n существует последовательность запусков, в которой tj присутствует по крайней мере n раз.
Уровень 3: Переход tj обладает активностью уровня 3, если существует бесконечная последовательность запусков, в которой tj присутствует неограниченно часто.
Уровень 4: Переход tj обладает активностью уровня 4, если для всякой 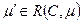 существует такая последовательность запусков σ, что tj разрешен в
существует такая последовательность запусков σ, что tj разрешен в 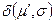 .
.
Переход, обладающий активностью уровня 0, называется пассивным. Переход, обладающий активностью уровня 4, называется активным. Сеть Петри обладает активностью уровня i, если каждый ее переход обладает активностью уровня i.
В качестве примера, иллюстрирующего уровни активности, рассмотрим сеть Петри на рис. 4.3. Переход t 0 не может быть запущен никогда; он пассивен. Переход t 1 можно запустить точно один раз; он обладает активностью уровня 1. Переход t 2 может быть запущен произвольное число раз, но это число зависит от числа запусков перехода t 3. Если мы хотим запустить t 2 пять раз, мы запускаем пять раз t 3 затем t 1 и после этого пять раз t 2. Однако, как только запустится t 1 (t 1 должен быть запущен до того, как будет запущен t 2), число возможных запусков t 2 станет фиксированным. Следовательно, t 2 обладает активностью уровня 2, но не уровня 3. С другой стороны, переход t 3 можно запускать бесконечное число раз, и поэтому он обладает активностью уровня 3, но не уровня 4, поскольку, как только запустится t 1, t 3 больше запустить будет нельзя.
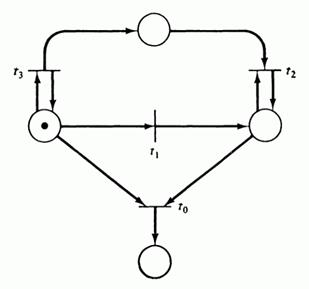
Рис 4.3: Пример различной степени активности переходов.
Задачи достижимости и покрываемости
Задача достижимости. Для данной сети Петри С с маркировкой m и маркировки m ' определить: 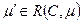 ?
?
Маркировка m " покрывает маркировку m ', если m " 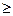 m ', т.е.
m ', т.е. 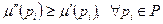 . Задача покрываемости. Для данной сети Петри С с начальной маркировкой m и маркировки m ' определить, существует ли такая достижимая маркировка
. Задача покрываемости. Для данной сети Петри С с начальной маркировкой m и маркировки m ' определить, существует ли такая достижимая маркировка 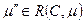 , такая что m "
, такая что m " 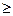 m '.
m '.
Методы анализа сетей Петри.
Дерево достижимости.
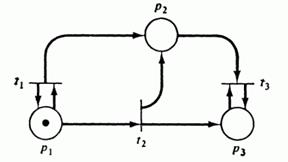
Рис 4.4: Маркированная сеть Петри, для которой строится дерево достижимости.
Дерево достижимости представляет множество достижимости сети Петри. Рассмотрим, например, маркированную сеть Петри на рис. 4.4. Её начальная маркировка – (1, 0, 0). Это – корневая вершина дерева достижимости. Непосредственно достижимые из неё маркировки – это вершины второго уровня и т.д.
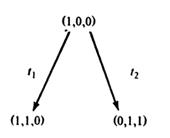
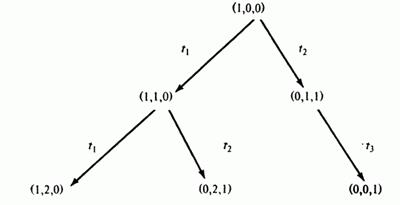
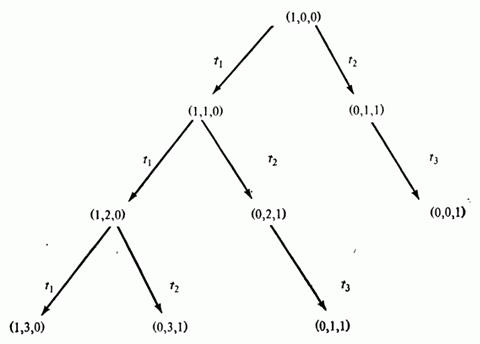
Рис 4.5: Первые три шага построения дерева достижимости для сети Петри на рис 4.4.
Получившееся дерево достижимости может оказаться бесконечным. Будет порождена каждая маркировка из множества достижимости, поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево.
Пассивные маркировки – маркировки, в которых нет разрешенных переходов. Они называются терминальными вершинами. Другой класс маркировок – это маркировки, ранее встречавшиеся в дереве. Они называются дублирующими вершинами; никакие последующие маркировки рассматривать нет нужды – все они будут порождены из места первого появления дублирующей маркировки в дереве. Таким образом, в дереве на рис.4.5 маркировка (0, 1, 1), получившаяся в результате выполнения последовательности 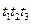 , не будет порождать какие-либо новые вершины, поскольку она ранее встречалась в дереве в результате выполнения перехода
, не будет порождать какие-либо новые вершины, поскольку она ранее встречалась в дереве в результате выполнения перехода 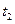 из начальной маркировки.
из начальной маркировки.
Для сведения дерева достижимости к конечному представлению используется еще одно средство. Рассмотрим последовательность запусков переходов σ, начинающуюся в начальной маркировке m и кончающуюся в маркировке m ' > m,. Маркировка m ' совпадает с маркировкой m, за исключением того, что имеет некоторые «дополнительные» фишки в некоторых позициях. Теперь, поскольку на запуски переходов лишние фишки не влияют, последовательность σ можно запустить снова, начиная в m ' и приходя к маркировке m ". В общем случае можно запустить последовательность σ n раз, получив в результате маркировку 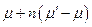 . Следовательно, для тех позиций, которые увеличивают число фишек последовательностью σ, можно создать произвольно большое число фишек, просто повторяя последовательность σ столько, сколько это нужно. В сети Петри на рис. 4.4, например, можно запустить переход
. Следовательно, для тех позиций, которые увеличивают число фишек последовательностью σ, можно создать произвольно большое число фишек, просто повторяя последовательность σ столько, сколько это нужно. В сети Петри на рис. 4.4, например, можно запустить переход 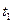 столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в р 2. Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа ω, который обозначает «бесконечность». Для любого постоянного а определим
столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в р 2. Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа ω, который обозначает «бесконечность». Для любого постоянного а определим
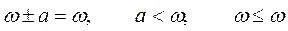 . (4.5)
. (4.5)
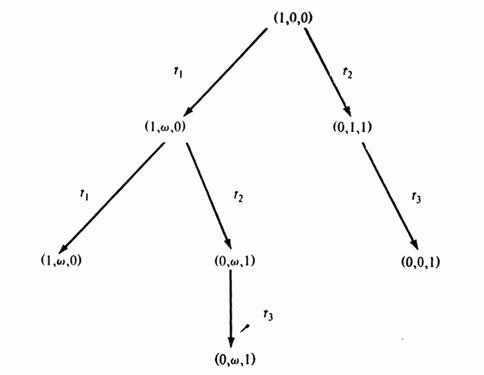
Рис 4.6: Дерево достижимости для сети Петри изображённой на рис 4.4.
Можно показать, что алгоритм построения дерева достижимости заканчивает работу.
Date: 2015-09-05; view: 2015; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |