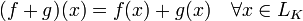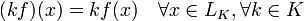Линейные отображение в ЛВП. Предоставление линейных преобразований матрицами

Лине́йное отображе́ние, лине́йный опера́тор — обобщение линейной числовой функции (точнее, функции y = kx) на случай более общего множества аргументов и значений. Линейные операторы, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.

Лине́йным отображе́нием векторного пространства L_K над полем K в векторное пространство M_K (лине́йным опера́тором из L_K в M_K) над тем же полем K называется отображение

,

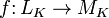удовлетворяющее условию линейности f (x + y) = f (x) + f (y), f (α x) = α f (x).

для всех 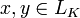и .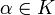

Если определить операции сложения и умножения на скаляр из основного поля K как

множество всех линейных отображений из L_K в M_K превращается в векторное пространство, которое обычно обозначается как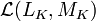

• Линейный функционал — линейный оператор, для которого M = K:
  
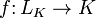
• Эндоморфизм — линейный оператор, для которого L = M:
  
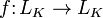
• Тождественный оператор — оператор , отображающий каждый элемент пространства в себя.
• Нулевой оператор — оператор, переводящий каждый элемент L_K в нулевой элемент M_K.
• Проектор - оператор сопоставляющий каждому x его проекцию на подпространство.
• Сопряжённый оператор к оператору 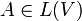— оператор A ^* на V ^*, заданный соотношением (A ^* f, x): = (f, Ax).
• Самосопряжённый оператор — оператор, совпадающий со своим сопряжённым оператором. Иногда такие операторы называют гипермаксимальными эрмитовыми.
• Эрмитов (или симметрический) оператор — такой оператор A, что (Ax, y) = (x, Ay) для всех пар x, y из области определения A. Для всюду определённых операторов совпадает с самосопряжённым.
• Положительно определённый оператор. Пусть L_K, M_K - гильбертовы пространства. Тогда линейный оператор называется положительным, если .

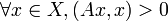Линейное преобразование переменных x₁, x₂,..., x_n — замена этих переменных на новые x"₁, x’₂,..., x"_n, через которые первоначальные переменные выражаются линейно, т. е. по формулам:
x₁ = a₁₁x’₁ + a₁₂x’₂ +... + a_nnx’_n + b₁,
x₂ = a₂₁x’₁ + a₂₂x’₂ +... + a_2nx’_n + b₂,
...
x_n = a_n1x’₁ + _an2x’₂ +... + a_nnx’_n + b_n,
здесь a_ij и b_i (i, j = 1,2,..., n) — произвольные числовые коэффициенты. Если b₁, b₂,..., b_n все равны нулю, то Линейное преобразование переменных называют однородным.
Простейшим примером Линейное преобразование переменных могут служить формулы преобразования прямоугольных координат на плоскости
х = x" cos a - y" sin a + a,
у = x" sin a + y" cos a + b.

Если определитель D = ½ a_ij ½, составленный из коэффициентов при переменных, не равен нулю, то можно и новые переменные x"₁, x"₂,..., x"_n линейно выразить через старые. Например, для формул преобразования прямоугольных координат

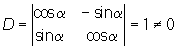
x’ =x cos a + ysin a + a₁
y’ = -x sin a + cos a + b₁
где a₁ = - a cos a - b sin a, b₂ = a sin a - b cos (. Другими примерами Линейное преобразование переменных могут служить преобразования аффинных и однородных проективных координат, замена переменных при преобразовании квадратичных форм и т. п.
Линейное преобразование векторов (или Линейное преобразование векторного пространства) называют закон, по которому вектору х из n -мерного пространства ставят в соответствие новый вектор x ", координаты которого линейно и однородно выражаются через координаты вектора х:
x’₁ = a₁₁x₁ + a₁₂x₂ +... +a_1nx_n
x’₂ = a₂₁x₁ + a₂₂x₂ +... +a_2nx_n

...
x’_n = a_n1x₁ + a_n2x₂ +... +a_nnx_n,
или коротко
x" = Ax.
Например, операция проектирования на одну из координатных плоскостей (пусть на плоскость хОу) будет Линейное преобразование трёхмерного векторного пространства: каждому вектору а с координатами х, у, z сопоставляется новый вектор b, координаты x", y"., z" которого выражаются через х, у, z следующим образом: x" = х, y" = у, z" = 0. Пример Линейное преобразование плоскости — поворот её на угол a вокруг начала координат. Матрицу
,
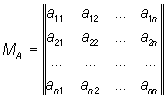составленную из коэффициентов Линейное преобразование А, называют его матрицей. Матрицами приведённых выше Линейное преобразование проектирования и поворота будут соответственно
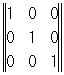и .
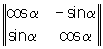Линейное преобразование векторного пространства можно определить (как обычно поступают) без использования системы координат: соответствие х ® у = Ax называют Линейное преобразование, если выполняются условия А (х + у) = Ax + Ау и A (a x) = a А (х) для любых векторов х и у и любого числа a. В разных системах координат одному и тому же Линейное преобразование будут соответствовать разные матрицы и, следовательно, разные формулы для преобразования координат.

К Линейное преобразование относится, в частности, нулевое Линейное преобразование О, переводящее все векторы в 0 (нулевой вектор): Ox = 0 и единичное Линейное преобразование Е, оставляющее все векторы без изменения: Ex = х; этим Л. и. в любой системе координат соответствуют нулевая и единичная матрицы.
Для Линейное преобразование векторного пространства естественным образом определяются операции сложения и умножения: суммой двух Линейное преобразование А и В называют Линейное преобразование С, переводящее любой вектор х в вектор Cx = Ax + Вх; произведением Линейное преобразование А и В называют результат их последовательного применения: С = AB, если Cx = А (В х).

В силу этих определений совокупность всех Линейное преобразование векторного пространства образует кольцо. Матрица суммы (произведения) Линейное преобразование равна сумме (произведению) матриц Линейное преобразование слагаемых (сомножителей); при этом существен порядок множителей, так как произведение Л. и., как и матриц, не обладает свойством коммутативности. Линейное преобразование можно также умножать на числа: если Линейное преобразование А переводит вектор х в вектор у = Ax, то a А переводит х в a у. Примеры операций над Линейное преобразование: 1) Пусть А и В означают операции проектирования па оси Ox и Оу в трёхмерном пространстве; А + В будет проектированием на плоскость хОу, а AB = 0. 2) А и В — повороты плоскости вокруг начала координат на углы j и 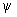; AB будет поворотом на угол j + 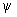. 3) Произведение единичного Линейное преобразование Е на число a будет преобразованием подобия с коэффициентом растяжения (или сжатия) a.

Линейное преобразование В называют обратным к Линейное преобразование А (и обозначают А ^-1), если BA = Е (или AB = Е). Если Линейное преобразование А переводило вектор х в вектор у, то Линейное преобразование А^{- 1} переводит у обратно в х. Линейное преобразование, обладающее обратным, называют невырожденным; такие Линейное преобразование характеризуются также тем, что определитель их матрицы не равен нулю. Некоторые классы Линейное преобразование заслуживают особого упоминания. Обобщением поворотов двумерных и трёхмерных евклидовых пространств являются ортогональные (или унитарные — в комплексных пространствах) Линейное преобразование Ортогональные Линейное преобразование не изменяют длин векторов (а следовательно, и углов между ними). Матрицы этих Линейное преобразование в ортонормированной системе координат также называются ортогональными (унитарными): произведение ортогональной матрицы на её транспонированную даёт единичную матрицу: å_ka_ika_jk = å_ka_kia_kj = 0 при i ¹ j, å_ka²_ik = å_ka²_ki = 1 (в комплексном пространстве å_ka_{ik 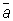jk} = å_ka_{ki 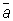kj} = 0, å_k|a_jk|² = å_k|a_ki|² = 1). Симметрическим (эрмитовым, или самосопряжённым, — в комплексном пространстве) Линейное преобразование называют такое Линейное преобразование, матрица которого симметрическая: a_ij = a_ji (или (a_ij = 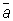_ij). Симметрические Линейное преобразование осуществляют растяжение пространства с разными коэффициентами по неск. взаимно ортогональным направлениям. С симметрическими Линейное преобразование связана теория квадратичных форм (или эрмитовых форм в комплексном пространстве).

Приведённое выше определение Линейное преобразование в векторном пространстве, не использующее координатную систему, без всяких изменений распространяется и на бесконечномерные (в частности, функциональные) пространства. Линейное преобразование в бесконечномерных пространствах принято называть линейными операторами.