
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Д. Если полученное дерево не обладает минимальной избыточностью, то и порождающее его дерево не обладает минимальной избыточностью. Пришли к противоречию. Ч.Т.Д
Д. Пусть произвольное слово А в алфавите А закодировано словом В с использованием схемы Σ(), для которой не выполняется свойство префикса, а для (Σ) это свойство выполняется. Выделим элементарные коды в соответствии со схемой Σ(), заменим их кодами схемы (Σ). Согласно теореме 4.1 полученное слово имеет единственную расшифровку. Следовательно, единственную расшифровку имеет слово В. Ч.Т.Д.
Т4.3. Алфавитное кодирование со схемой кодирования Σ не обладает свойством однозначности, если и только если граф G(Σ) содержит ориентированный цикл, проходящий через вершину L.
Доказательство приведено в [1]
Т4.7. Для всякого кода с минимальной избыточностью сущ-ет насыщенное дерево, его представляющее.
Д. Преобразования 1, 2 позволяют любое кодовое дерево, в том числе и кодовое дерево, обладающее минимальной избыточностью, привести к насыщенному дереву, не увеличивая при этом избыточности кодового дерева. Ч.Т.Д..
Т4.8. Для кода с минимальной избыточностью существует приведенное насыщенное дерево.
Доказательство следует из определения приведенного насыщенного дерева
Т4.9. Операция редукции порождает новое кодовое дерево с минимальной избыточностью.
Д. Если полученное дерево не обладает минимальной избыточностью, то и порождающее его дерево не обладает минимальной избыточностью. Пришли к противоречию. Ч.Т.Д.
Т5.1. Множество S не выполнимо, если и только если не выполнимы два множества: 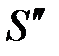 È
È 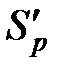 и
и 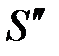 È
È 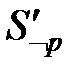 .
.
Доказательство следует из того факта, что рассматриваемые множества получаются из S фиксированием значения p (p = и, p = л соответственно).
Т4.4 (неравенство МакМилана). Если кодирование со схемой Σ обладает свойством однозначности, то выполняется соотношение 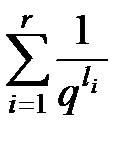 £ 1.
£ 1.
Д. Рассмотрим всевозможные слова в алфавите А, имеющие длину n. Представим их выражением:
(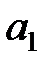 +…+
+…+ 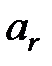 )
) 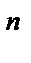 . (1)
. (1)
Произвольное слово длины n в алфавите А можно представить в виде 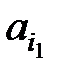 ,
, 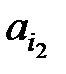 ,…,
,…, 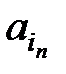 . Здесь
. Здесь 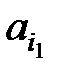 принадлежит первой из n скобок,
принадлежит первой из n скобок, 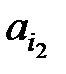 – второй и т.д. Имея это в виду, запишем соотношение
– второй и т.д. Имея это в виду, запишем соотношение
(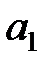 +…+
+…+ 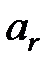 )
) 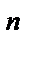 =
= 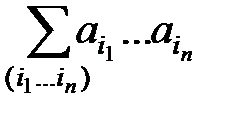 . (2)
. (2)
Сопоставим рассматриваемым словам коды в алфавите В. Коды получаются заменой симв. 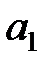 ,…,
,…, 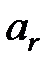 элементарными кодами
элементарными кодами 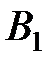 ,…,
,…, 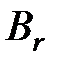 соответственно. Имеем
соответственно. Имеем
(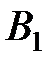 +…+
+…+ 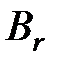 )
) 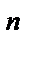 =
= 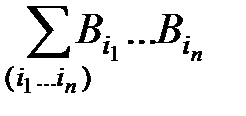 . (3)
. (3)
В силу однозначности кодирования, если ( ,…,
,…, 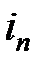 ) ¹ (
) ¹ (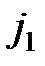 ,…,
,…, 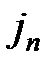 ), то
), то 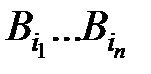 ¹
¹ 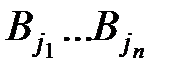 , то есть разным словам в алфавите А соответствуют разн. слова в алфавите В.
, то есть разным словам в алфавите А соответствуют разн. слова в алфавите В.
Соотношению (3) соответствует тождество
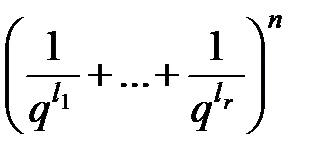 =
= 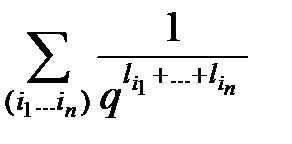 .(4)
.(4)
Слагаемым правой части, имеющим одинаковые знаменатели, сопоставляются слова 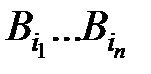 одинаковой длины t, t =
одинаковой длины t, t = 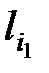 +…+
+…+ 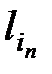 . Пусть ν(n, t) – число слов
. Пусть ν(n, t) – число слов 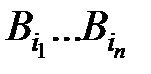 из (3), имеющих длину t. Пусть l =
из (3), имеющих длину t. Пусть l = 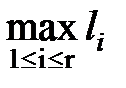 . Тогда
. Тогда
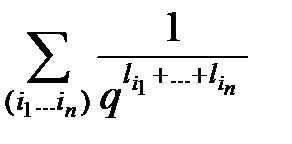 =
= 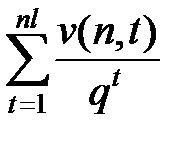 . (5)
. (5)
Из однозначности кодирования следует ν(n, t) £ 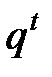 . (6)
. (6)
Действительно, 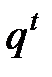 есть число всевозможных слов длины t в алфавите В. Поскольку в (3) все рассматриваемые коды слов длины n в алфавите А различны, то различны и их подмножества – коды одной и той же длины. Следовательно, соотношение (6) выполняется.
есть число всевозможных слов длины t в алфавите В. Поскольку в (3) все рассматриваемые коды слов длины n в алфавите А различны, то различны и их подмножества – коды одной и той же длины. Следовательно, соотношение (6) выполняется.
Далее 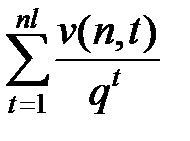 £ nl. Тогда
£ nl. Тогда  £
£ 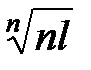 .
.
Это неравенство справедливо для любого n, так как его левая часть не зависит от n. Перейдя к пределу при n ®¥, получим неравенство МакМилана
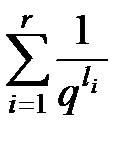 £ 1. Ч.Т.Д.
£ 1. Ч.Т.Д.
Теорема 5.2. Пусть 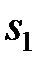 ,
, 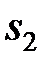 – дизъюнкты КНФ, представленной множеством S, а l – литера. Если l из
– дизъюнкты КНФ, представленной множеством S, а l – литера. Если l из 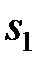 , а Ø l из
, а Ø l из 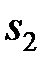 , то дизъюнкт r =(
, то дизъюнкт r =(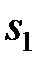 / {l}) Ú (
/ {l}) Ú (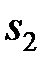 / {Ø l }) есть логическое следствие множества S дизъюнктов. Доказательство следует из введенного ранее определения резольвенты.
/ {Ø l }) есть логическое следствие множества S дизъюнктов. Доказательство следует из введенного ранее определения резольвенты.
С. КНФ, представленные множествами S и S È r, эквивалентны.
Т4.5. Если алфавитное кодирование, заданное схемой Σ, однозначно, Σ:
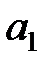
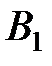 , …
, … 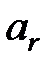
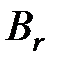 ,
,
то существует алфавитное кодирование, задаваемое схемой 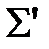 :
:
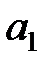
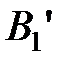 , …
, … 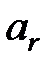
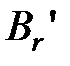 ,
,
обладающее свойством префикса, причем для элементар. кодов 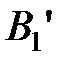 ,…,
,…, 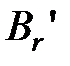 выполняются равенства
выполняются равенства
l (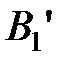 ) = l (
) = l (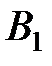 ), … l (
), … l (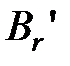 ) = l (
) = l (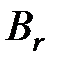 ).
).
Д. Пусть 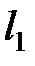 £…£
£…£ 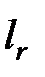 . Воспользуемся неравенством МакМилана
. Воспользуемся неравенством МакМилана 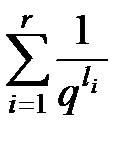 £ 1.
£ 1.
Разобьем числа 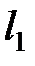 ,…,
,…, 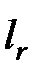 , представляющ. длины элементарных кодов, на классы равной длины. Пусть μ – число классов 1 £ μ £ r;
, представляющ. длины элементарных кодов, на классы равной длины. Пусть μ – число классов 1 £ μ £ r; 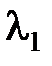 ,…,
,…, 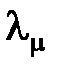 – длины элементов классов;
– длины элементов классов; 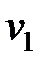 ,…,
,…, 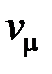 – мощности классов. Перепишем неравенство МакМилана с учетом введенных обозначений:
– мощности классов. Перепишем неравенство МакМилана с учетом введенных обозначений:
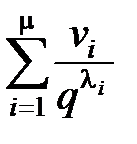 £ 1.
£ 1.
Это неравенство порождает серию вспомогательных неравенств:
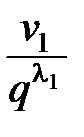 £ 1 или
£ 1 или 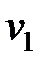 £
£ 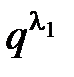 ,
,
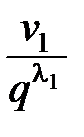 +
+ 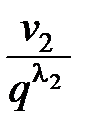 £ 1 или
£ 1 или 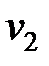 £
£ 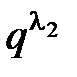 –
– 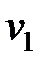
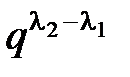 ,
,
…
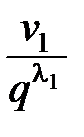 +
+ 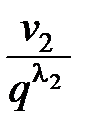 +…+
+…+ 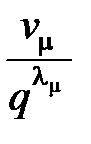 £ 1 или
£ 1 или 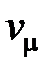 £
£ 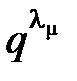 –
– 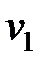
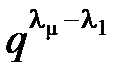 –
– 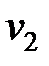
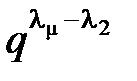 –…–
–…– 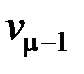
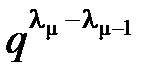 .
.
Рассмотрим слова в алфавите B, имеющие длину 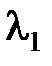 . Так как
. Так как 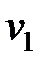 £
£ 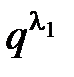 , то можно выбрать из них
, то можно выбрать из них 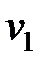 слов длины
слов длины 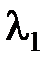 . Обозначим выбранные слова через
. Обозначим выбранные слова через 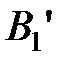 ,…,
,…, 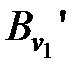 . Они представляют элементарные коды схемы кодирования
. Они представляют элементарные коды схемы кодирования 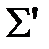 . Исключим из рассмотрения в дальнейшем слова, начинающиеся с
. Исключим из рассмотрения в дальнейшем слова, начинающиеся с 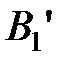 ,…,
,…, 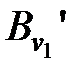 . Выберем слова в алфавите В, имеющие длину
. Выберем слова в алфавите В, имеющие длину 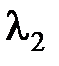 и не начинающиеся со слов
и не начинающиеся со слов 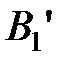 ,…,
,…, 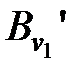 . Число таких слов в алфавите В определяется выражением
. Число таких слов в алфавите В определяется выражением
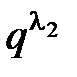 –
– 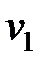
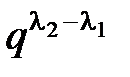 .Так как
.Так как 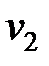 £
£ 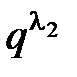 –
– 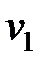
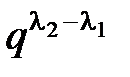 , то имеется возможность выбрать
, то имеется возможность выбрать 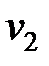 нужных нам слов. Обозначим их через
нужных нам слов. Обозначим их через 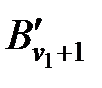 ,…,
,…, 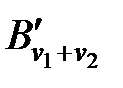 . Они также представл. Элементарн коды схемы кодирования
. Они также представл. Элементарн коды схемы кодирования 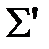
Исключим в дальнейшем слова, начинающиеся с уже включенных в схему 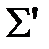 элементарных кодов. В конце концов мы получим все элементарные коды
элементарных кодов. В конце концов мы получим все элементарные коды 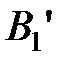 ,…,
,…, 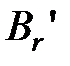 схемы
схемы 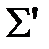 . Из построения кодов следует:
. Из построения кодов следует:
l (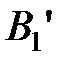 ) = l (
) = l (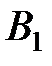 ),…, l (
),…, l (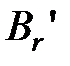 ) = l (
) = l (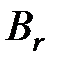 ). Ч.Т.Д.
). Ч.Т.Д.
Т4.6. Для кода с минимальной избыточностью из условия 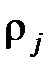 <
< 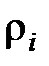 следует, что
следует, что 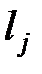 ³
³ 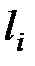 .
.
Д. Предпол противное: 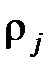 <
< 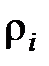 и
и 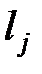 <
< 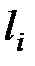 Тогда, если в схеме Σ:
Тогда, если в схеме Σ:
| … | … |

| 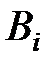
|
| … | … |
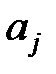
| 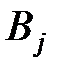
|
| … | … |
поменять местами коды 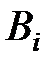 ,
, 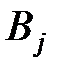 , то получим схему
, то получим схему 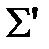 :
:
| … | … |
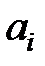
| 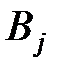
|
| … | … |
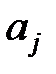
| 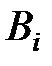
|
| … | … |
имеющую меньшую избыточность 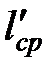 , чем
, чем 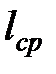 . В самом деле,
. В самом деле,
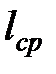 –
– 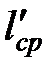 = (
= (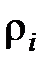
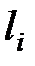 +
+ 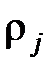
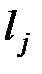 ) – (
) – (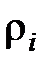
 +
+ 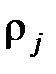
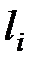 ) =
) =
= (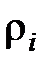 –
– 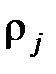 )(
)(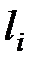 –
–  ) > 0.
) > 0.
Это противоречит условию минимальной избыточности схемы кодирования Σ. Ч.Т.Д.
Сл. В кодовом дереве для кода с минимальной избыточностью вероятности, приписываемые вершинам яруса 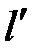 , не меньше вероятностей, приписываемых вершинам яруса
, не меньше вероятностей, приписываемых вершинам яруса 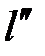 , если
, если 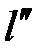 >
> 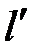 .
.
Date: 2015-09-05; view: 509; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |