Гипотеза Прокла:с какой целью Евклид написал свои «Начала»?

В настоящее время каждый школьник знает, кто такой Евклид, который написал самое значительное математическое сочинение греческой эпохи – Начала Евклида. Это научное произведение создано им в 3 в. до н. э. и содержит основы античной математики: элементарную геометрию, теорию чисел, алгебру, теорию пропорций и отношений, методы определения площадей и объемов и др. Евклид подвел в этом сочинении итог трехсотлетнему развитию греческой математики и создал прочный фундамент для дальнейшего развития математики. Начала Евклида состоят из тринадцати книг. Любопытно, что XIII-я, то есть, заключительная книга Начал посвящена изложению теории пяти правильных многогранников (Платоновых тел). В этой Книге доказывается, что иных правильных выпуклых тел не существует. Суть этого доказательства состоит в следующем. Простейшая из граней правильного многогранника – это равносторонний треугольник с углами 60°. Если число треугольников шесть, то сумма плоских углов, примыкающих к вершине многогранника, равна 360°. Поэтому правильный выпуклый многогранник с треугольными гранями можно построить только из трех, четырех или пяти треугольников.

Если грань – это квадрат с углами 90°, то многогранный угол, меньший 360°, составляется лишь из трех граней. Аналогично, в одной вершине правильного многоугольника могут сходиться только три пятиугольные грани с углами 108°. Грани не могут иметь форму шестиугольника, так как, совместив в пространстве три шестиугольника с внутренними углами 120°, мы получили бы в сумме угол 360°.

Анализ Начал приводит к постановке следующих вопросов. Почему изложение геометрической теории Платоновых тел Евклид разместил в XIII- й, то есть, заключительной главе своего знаменитого математического сочинения? Ведь обычно в заключительной части размещают наиболее важные результаты научного произведения. Не содержится ли в этом факте какая - то тайна, какой - то намек, который может изменить наш взгляд на Начала Евклида?

С последним вопросом связан еще один вопрос: с какой целью Евклид написал свои Начала? На первый взгляд, кажется, что ответ на последний вопрос очень простой: главная цель Евклида состояла в том, чтобы изложить основные достижения греческой математики за 300 лет, предшествующих Евклиду, используя «аксиоматический метод» изложения материала. Действительно, Начала Евклида являются главным трудом греческой науки, посвященным аксиоматическому построению геометрии и математики. Такой взгляд на Начала наиболее распространен в современной математике.

Однако, кроме «аксиоматической» точки зрения существует и другая точка зрения на мотивы, которыми руководствовался Евклид при написании «Начал». Эта точка зрения высказана греческим философом и математиком Проклом Диадохом (412-485), одним из первых комментаторов Начал.

Среди математических сочинений Прокла наиболее известным является его «Комментарий к первой книге «Начал» Евклида». В этом Комментарии Прокл выдвигает следующую необычную гипотезу. Как упоминалось, XIII-я, то есть, заключительная книга Начал посвящена изложению теории пяти правильных многогранников, которые играли главенствующую роль в «Космологии Платона» и в современной науке известны под названием Платоновых тел. Именно на это обстоятельство и обращает внимание Прокл. Как подчеркивает Эдуард Сороко [1], по мнению Прокла, Евклид « создавал « Начала » якобы не с целью изложения геометрии как таковой, а чтобы дать полную систематизированную теорию построения пяти « Платоновых тел », попутно осветив некоторые новейшие достижения математики ».

А это уже сенсация! Прокл утверждает, что главная цель Евклида состояла в том, чтобы построить геометрическую теорию Платоновых тел. Все предшествующие главы Начал - это лишь «сопутствующий материал», направленный на достижение главной цели. Чем же прославились Платоновы тела, чтобы им посвящать специальное математическое сочинение, да еще такое, как Начала Евклида? Для этого необходимо вспомнить ту роль, которую Платоновы тела играли в греческой науке. Как известно, главная идея всей древнегреческой науки – это идея Гармонии. Впервые она была сформулирована Пифагором в его Учении о числовой гармонии мироздания. Дальнейшее развитие она получила в сочинениях Платона. Платоновы тела занимали важное место в философской концепции Платона об устройстве мироздания. Четыре многогранника олицетворяли в ней четыре сущности или "стихии". Платон считал, что атомы этих стихий имеют форму правильных многогранников. При этом Тетраэдр символизировал Огонь, так как его вершина устремлена вверх; Икосаэдр - Воду, так как он самый "обтекаемый" многогранник; Куб - Землю, как самый "устойчивый" многогранник; Октаэдр - Воздух, как самый "воздушный" многогранник; пятый же многогранник, Додекаэдр, символизировал все мироздание, его по латыни стали называть quinta essentia («пятая сущность»). Он воплощал в себе "все сущее", «Вселенский разум», символизировал все мироздание и считался главной геометрической фигурой мироздания.

Главный вывод из «гипотезы Прокла» состоит в том, что Начала Евклида, величайшее греческое математическое сочинение, было написано Евклидом под непосредственным влиянием греческой идеи гармонии, которая основывалась у древних греков на Платоновых телах. Таким образом, «гипотеза Прокла» позволяет высказать предположение, что хорошо известные в античной науке " Пифагорейская доктрина о числовой гармонии Мироздания » и « Космология Платона », основанная на правильных многогранниках, были воплощены в величайшем математическом сочинении греческой математики, Началах Евклида. С этой точки зрения можно рассматривать Начала Евклида как первую попытку создать Математическую теорию гармонии мироздания, которая ассоциировалась в античной науке с Платоновыми телами. Это и есть главная тайна Начал Евклида, которая приводит к пересмотру истории развития математики, начиная с Евклида.

К сожалению, оригинальная гипотеза Прокла, касающаяся истинных целей, которые преследовал Евклид при написании Начал, проигнорирована большинством современных историков математики. Это привело к искаженному взгляду на структуру математики, всего математического образования и истории ее развития. И это является одной из «стратегических ошибок» в развитии математики.

5. Новый взгляд на развитие математики, вытекающий из гипотезы Прокла

Что такое математика? Каковы ее происхождение и история? В чем состоит связь математики с другими научными дисциплинами и в чем состоит отличие математики от других наук? Когда возникла математика? Какие практические проблемы и задачи стимулировали развитие математики на этапе ее зарождения? Блестящий ответ на этот вопрос можно найти в книге выдающегося математика А. Н. Колмогорова [5]. Колмогоров пишет: «Ясное понимание самостоятельного положения математики как особой науки, имеющей собственный предмет и метод, стало возможным только после накопления достаточно большого фактического материала и возникло впервые в Древней Греции в 6-5 вв. до н.э. Развитие математики до этого времени естественно отнести к периоду зарождения математики, а к 6-5 вв. до н.э. приурочить начало периода элементарной математики. В течение этих двух первых периодов математического исследования имеют дело почти исключительно с весьма ограниченным запасом основных понятий, возникших еще на очень ранних ступенях исторического развития в связи с самыми простыми запросами хозяйственной жизни, сводившимися к счету предметов, измерению количества продуктов, площадей земельных участков, определению размеров отдельных частей архитектурных сооружений, измерению времени, коммерческим расчетам и т.п. Первые шаги механики и физики (за исключением отдельных исследований греческого ученого Архимеда (3 в. до н.э.), требовавших уже начатков исчисления бесконечно малых) могла еще удовлетвориться этим же запасом основных математических понятий. Единственной наукой, которая задолго до широкого развития математического изучения явлений природы в 17-18 вв. систематически предъявляла математике свои особые и очень большие требования, была астрономия, целиком обусловившая, например, раннее развитие тригонометрии. Запас понятий, с которыми имела дело математика до начала 17 в., составляет и до настоящего времени основу «элементарной математики», преподаваемой в начальной и средней школе».

В этом высказывании великого математика в концентрированном виде сформулированы и выделены все основные проблемы развития математики на начальном этапе ее развития:

1. Выделено два важных периода в развитии математики на этапе ее становления как
самостоятельной науки: этап зарождения математики (догреческий период) и этап
элементарной математики (от греческой математики 6-5 вв. до н.э. и до начала 17 в.).

2. Выделены две главные практические задачи, которые стимулировали развитие
математики на этапе ее зарождения. Это – задача счета и задача измерения.

3. Отмечена роль астрономии в развитии математики на этапе зарождения, в частности, в
создании такой важной математической дисциплины как тригонометрия.

4. Подчеркнуто, что математика как особая наука, имеющая собственный предмет и метод, была создана в Древней Греции в 6-5 вв. до н.э.

5. Отмечено, что математические знания, полученные в период элементарной математики (от 6-5 вв. до н.э. и до начала 17 в.), составляют основу школьного математического образования.

Общепринятой является точка зрения, что создание математики связано с потребностями практики, которые стимулировали развитие математики с периода ее зарождения. Как упоминалось, академик Колмогоров в книге [5] выделил две главные, то есть, «ключевые» проблемы, которые стимулировали развитие математики на этапе ее зарождения - проблему счета и проблему измерения. Уже на раннем этапе развития проблемы счета было сделано выдающееся математическое открытие в этой области: позиционный принцип представления чисел (Вавилон). Этот принцип лежит в основе всех известных систем счисления, в частности, десятичной и двоичной, которая лежит в основе информатики. Развитие «проблемы счета» привело, в конечном итоге, к формированию понятия натурального числа, которое является первым фундаментальным понятием математики. Решение задач, связанных с измерением геометрических величин, привела к созданию геометрии, а открытие пифагорейцами несоизмеримых отрезков привело к формированию понятия иррационального числа, которое считается еще одним фундаментальным понятием математики.

К сожалению, А.И. Колмогоров в своей книге [5] не придал особого значения «гипотезе Прокла». Он о ней даже не упоминает. Вполне допустимо, что он о ней вообще не знал, как и многие современные математики. Такое отношение к «гипотезе Прокла» вполне объяснимо, если учесть скептическое отношение многих математиков к Платоновым телам, а тем более – к «золотому сечению». А «гипотеза Прокла» нацелена именно на эти математические открытия античной математики и выдвигает их на первые роли в Началах Евклида и во всей древнегреческой математике. Из «гипотезы Прокла» вытекают следующие необычные выводы, касающиеся развития математики и которые ну никак не могут быть восприняты представителями «классической математики», включая и академика Колмогорова.

Вряд ли кто-либо будет спорить, что Начала Евклида являются неисчерпаемым источником развития современной математики, а современное школьное математическое образование имеет структуру Начал Евклида. Но согласно Проклу, Начала были написаны Евклидом под непосредственным влиянием проблемы гармонии, которая ассоциировалась с «Платоновыми телами» и «золотым сечением» - важнейшими математическими открытиями античной математики (Предложение II.11 Начал Евклида). Именно эта проблема была положена Евклидом в основу Начал, главной целью которых было создание геометрической теории «Платоновых тел», которые в «космологии Платона» выражали гармонию Мироздания. Поэтому мы имеем право полагать, что проблема гармонии и связанные с ней Платоновы тела сыграла в развитии математики не меньшую роль, чем проблема счета, которая привела к формированию понятия натурального числа, и проблема измерения, развитие которой («несоизмеримые отрезки») привело к открытию иррациональных чисел.

Таким образом, развитие каждой из ключевых проблем математики привело к формированию трех важнейших понятий математики: натуральных чисел, иррациональных чисел и Платоновых тел. И такой подход приводит нас к новому взгляду на развитие математики, представленному на Рис. 2.

Возникает вопрос, как сформулированные выше проблемы (счета, измерения и гармонии») отражены в Началах Евклида? Оказывается, самым непосредственным образом. Начала Евклида построены по дедуктивной системе: сначала (Книга I) приводятся определения, постулаты и аксиомы, затем формулировки теорем и их доказательства. Вслед за определением основных геометрических понятий и объектов (например, точки, прямой) Евклид доказывает существование остальных объектов геометрии (например, равностороннего треугольника) путём их построения, которое выполняется на основе пяти постулатов. В постулатах утверждается возможность выполнения некоторых элементарных построений, например «что от всякой точки до всякой точки (можно) провести прямую линию» (1 постулат); «И что от всякого центра и всяким раствором (может быть) описан круг» (III постулат). Особое место среди постулатов занимает V постулат (аксиома о параллельных): «И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные эти прямые неограниченно встретятся с той стороной, где углы меньше двух прямых ». Напомним, что именно анализ этого постулата привел к наиболее крупному математическому открытию – геометрии Лобачевского, с которой, по мнению Колмогорова, и начинается период современной математики.

Постулаты изложены в начале Книги I, в которой, кроме этого, рассматриваются основные свойства треугольников, прямоугольников, параллелограммов и производится сравнение их площадей. Заканчивается Книга I знаменитой Теоремой Пифагора.

В Книге II излагается так называемая геометрическая алгебра, т. е. строится геометрический аппарат для решения задач, сводящихся к квадратным уравнениям. Но не во всех источниках упоминается, что в Книге II Евклид зачем-то поместил « задачу о делении отрезка в крайнем и среднем отношении » (Предложение II.11), которая в современной науке называется « золотым сечением ».

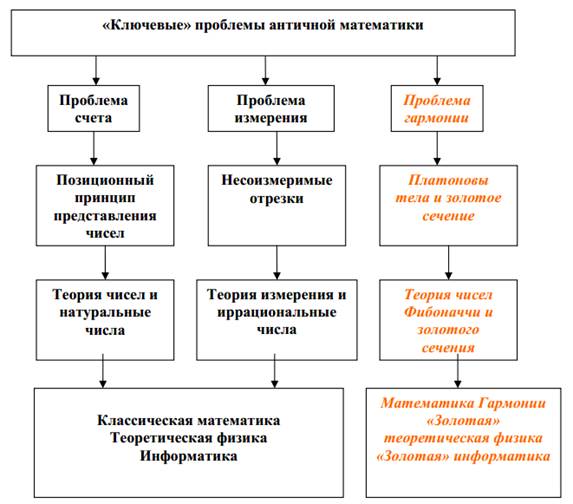
Рисунок 2. «Ключевые» проблемы античной математики и новый взгляд на пути развития математики, начиная с Евклида

Значительная часть Начал посвящена изложению теории иррациональностей, восходящей к несоизмеримым отрезкам и основанной на «методе исчерпывания » Евдокса. В Книге V излагается общая теория отношений величин, созданная Евдоксом; её можно рассматривать как прообраз теории действительных чисел, разработанной только во 2-й половине 19 в. Общая теория отношений является основой учения о подобии (Книга VI) и метода исчерпывания (Книга VII), также восходящих к Евдоксу. В Книгах VII—IX изложены начала теории чисел. В эти книги входят: алгоритм Евклида и теория делимости, включая теоремы об однозначности разложения целого числа на простые множители и о бесконечности числа простых чисел; здесь излагается также учение об отношении целых чисел, эквивалентное, по существу, теории рациональных (положительных) чисел. В Книге Х даётся классификация квадратичных и биквадратичных иррациональностей и обосновываются некоторые правила их преобразования. Результаты Книги Х применяются в Книге XIII для нахождения длин рёбер правильных многогранников. Значительная часть Книг Х и XIII (вероятно и VII) принадлежит Теэтету (начало 4 в. до н. э.). В Книге XI излагаются основы стереометрии. В Книге XII определяются с помощью метода исчерпывания отношение площадей двух кругов и отношение объёмов пирамиды и призмы, конуса и цилиндра. Эти теоремы впервые доказаны Евдоксом. Наконец, в Книге XIII определяется отношение объёмов двух шаров, строятся пять правильных многогранников и доказывается, что иных правильных тел не существует.

Из проведенного анализа можно сделать следующие выводы, касающиеся роли фундаментальных понятий и теорий математики, изложенных в Началах:

1. Первый вывод состоит в том, что в Началах Евклида впервые изложены основы теории чисел, к которой восходит современная теория чисел. Эта теория основана на следующем определении натурального числа, введенного Евклидом:

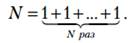
Основываясь на этом определении, в Началах впервые были изложены следующие классические результаты теории чисел: алгоритм Евклида, теорема об однозначности разложения целого числа на простые множители, теорема о бесконечности числа простых чисел и др.

2. Второй вывод состоит в том, что в Началах широко представлены основы теории иррациональностей. Здесь широко используется «метод исчерпывания» Евдокса, предложенный им для преодоления кризиса в основаниях математики, возникшего в связи с открытием «несоизмеримых отрезков». То есть, в Началах впервые излагается теория иррациональных чисел, восходящая к «несоизмеримым отрезкам».

3. Третий вывод касается Платоновых тел. Согласно «гипотезе Прокла», именно создание геометрической теории Платоновых тел и было главной целью Евклида при написании своих Начал. Учитывая ту роль, которую Платоновы тела играли в древнегреческой науке (Пифагор, Платон, Евклид), мы имеем полное право причислить Платоновы тела к разряду выдающихся математических открытий античной науки.

4. Еще один вывод касается роли « золотого сечения » в Началах Евклида. Как известно, «золотое сечение» стало своеобразным каноном древнегреческой математики, науки и культуры. Чтобы не быть голословным, здесь уместно вспомнить широко известные высказывания астронома и математика Иоганна Кеплера и философа Алексея Лосева.

Иоганн Кеплер:

«В геометрии существует два сокровища - теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем».

В этом высказывании Кеплер ставит «золотое сечение» в один ряд с «Теоремой Пифагора» - одной из величайших геометрических теорем.

Алексей Лосев:

«Космос античным мыслителям периода зрелой классики представляется не просто некоей отвлеченной неопределенностью, (в таком случае он был бы только чистой мыслью), но совершенно живым и единораздельным телом, содержащим в себе нерушимую цельность, несмотря на бесконечные различия всех его проявлений. С точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления - золотого сечения (то есть, целое относится в нем к большей части, как большая часть к меньшей). Этому закону, кстати сказать, древние греки подчиняли и свои архитектурные сооружения. Их систему космических пропорций нередко в литературе изображают как курьезный результат безудержной и дикой фантазии. В такого рода объяснениях сквозит антинаучная беспомощность тех, кто это заявляет. Однако понять данный историко-эстетический феномен можно только в связи с целостным пониманием истории, то есть, используя диалектико-материалистическое представление о культуре и ища ответа в особенностях античного общественного бытия».

В этом высказывании Лосев выдвигает «золотое сечение» на уровень всеобщего закона природы.

Известно еще одно интересное высказывание Лосева, касающееся «золотого сечения»:

«Закон золотого деления должен быть диалектической необходимостью. Это – та мысль, которую, насколько мне известно, я провожу впервые».

Мы знаем, что гранями Платоновых тел могут быть только три вида правильных многоугольников: правильный треугольник (тетраэдр, октаэдр, икосаэдр), квадрат (куб) и правильный пятиугольник или пентагон (додекаэдр). Для того, чтобы сконструировать Платоновы тела, мы должны, прежде всего, уметь геометрически (то есть, с помощью линейки и циркуля) построить грани Платоновых тел. У Евклида не было никаких проблем с построением правильного или равностороннего треугольника и квадрата, однако, он столкнулся с определенными трудностями при конструировании правильного пятиугольника или пентагона, лежащего в основе додекаэдра. С помощью «золотого сечения» ему удалось это сделать.

В заключение приведем мнение выдающегося российского историка математики Мордухай-Болтовского, переводчика «Начал» Евклида на русский язык и комментатора Начал, по поводу места, занимаемого «золотым сечением» в Началах Евклида. Мордухай - Болтовский:

« Теперь посмотрим, какое место занимает золотое сечение в « Началах » Евклида. Прежде всего, нужно отметить, что оно встречается в двух формах, разница между которыми почти неощутима для нас, но была очень существенной в глазах греческого математика V-VI- го веков до н. э. Первая форма, прототип которого мы видели в Египте, является в Книге II « Начал », а именно в Предложении 11 вместе с вводящими его предложениями 5 и 6; здесь золотое сечение определяется как такое, в котором квадрат, построенный на большем отрезке, равняется прямоугольнику на всей прямой и меньшем отрезке. Вторую форму мы имеем в определении 3 книги VI, где золотое сечение определяется пропорцией – как вся прямая к большему отрезку, так и больший отрезок к меньшему - и называется делением в крайнем и среднем отношении; в этой форме золотое сечение могло быть известным только со времен только со времен Евдокса. Интересно отметить, что предложениям 5, 6 и 11 книги II соответствуют предложения 27, 28 и 30 – шестой. Затем, предложения 5 и 6 книги II разорвали связь между предложениями 4 и 7, соответствующим нашим формулам квадратов суммы и разности; « та же фигура », о которой упоминается в предложении 7, строится в 4- м.

В книге XIII золотое сечение является в обеих указанных формах, а именно в первой форме в предложениях 1-5 и во второй – в предложениях 8-10. Правда в формулировке и тексте доказательства 1-5 предложений встречаются слова « в крайнем и среднем отношении », в доказательствах есть некоторые следы пользования пропорциями, но при внимательном чтении нетрудно заметить, что все эти места не связаны органически с общим текстом и легко из него могут быть исключены; все доказательство по существу ведется исходя из равенства на большем отрезке прямоугольнику ... Более того, предложение 2 книги XIII по существу равнозначно геометрическому построению предложения 11 книги II.

Все это позволяет думать, что предложения 4, 7, 8 книги II и предложения 1-5 книги XIII представляют остатки одного из самых древних в истории греческой геометрии документов, восходящего по всей вероятности к первой половине V века и возникшего в

пифагорейской школе на основании того материала, который был привезен из Египта. Сравнительную древность этого документа можно установить из того обстоятельства, что предложения 4 и 7 книги II служат в ней для доказательства обобщенной теоремы Пифагора [ квадрат стороны против острого и тупого угла ( предложения 12 и 13 книги II)], которая, несомненно, была известна Гиппократу Хиосскому ... Несмотря на то, что первые пять предложений книги XIII составляют одно целое с рядом предложений книги II, нужно отметить, что при непосредственном использовании предложений книги II ( в особенности предложения 11, которое и дает построение золотого сечения ) доказательства были бы в отдельных случаях значительно проще »

Проведенный анализ, который находится в полном согласии с мнениями Кеплера, Лосева и Мордухай-Болтовского, дают нам основание утверждать, что «золотое сечение» может быть также причислено к разряду выдающихся математических открытий античной науки и вполне может быть поставлено в один ряд не только с «теоремой Пифагора» (Кеплер), но также и с другими выдающимися открытиями античной науки, в частности, с Платоновыми телами, натуральными и иррациональными числами. При этом мы никак не имеем права игнорировать мнение Иоганна Кеплера по поводу «золотого сечения» (побольше бы таких математиков в современной науке), а также мнение гения российской учености, выдающегося философа и мыслителя Алексея Лосева о том, что «с точки зрения Платона, да и вообще с точки зрения всей античной космологии мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления - золотого сечения ( то есть, целое относится в нем к большей части, как большая часть к меньшей )». Экспериментальное доказательство проявления «золотого сечения» в квантовом мире, сделанное английскими и немецкими физиками в 2010 г., завершает спор о роли «золотого сечения» в современной науке в пользу «золотого сечения» и подтверждает гениальную прозорливость Пифагора, Платона и Евклида.

Сформулированный выше подход (Рис. 2) приводит к выводу, который может оказаться неожиданным и, возможно, неприемлемым для многих математиков. Оказывается, что параллельно с « Классической Математикой » в науке, начиная с древних греков, развивалась еще одно математическое направление – « Математика Гармонии », которая, как и классическая математика, восходит к « Началам » Евклида, но акцентирует свое внимание не на « аксиоматическом подходе », а на геометрической « задаче о делении отрезка в крайнем и среднем отношении » ( Предложение II.11)и на теории правильных многогранников, изложенной в XIII-й книге « Начал » Евклида. И в развитии «Математики Гармонии» в течение нескольких тысячелетий принимали участие выдающиеся мыслители, ученые и математики: Пифагор, Платон, Евклид, Фибоначчи, Пачоли, Кеплер, Кассини, Бине, Люка, Клейн, а в 20-м веке – Воробьев и Хогатт. И против этих фактов возражать очень трудно. То есть, «Математика гармонии» - это, действительно, великое достижение древнегреческой науки и эта математика, созданная Пифагором и Платоном, по существу, и была воплощена в Началах Евклида!

В чем же заслуга Евклида в «теории золотого сечения»? Очевидно, в том, что он впервые связал Платоновы тела (в частности, додекаэдр и икосаэдр) с «золотым сечением». С Начал Евклида Платоновы тела и «золотое сечение» развиваются в науке в неразрывном единстве как два выразителя гармонии в окружающем нас мире, введенные еще в античный период. И это подтверждается нижеследующими историческими примерами и научными открытиями современной науки.

6. Платоновы тела и « золотое сечение » в « Божественной пропорции » Луки Пачоли

Особенно ярко связь Платоновых тел с «золотым сечением» обнаруживается в книге Луки Пачоли «Божественная пропорция» (1509 г.), которая была написана под непосредственным влиянием и даже участием Леонардо да Винчи. Историческое значение книги «Божественная пропорция» состоит в том, что это была первая в истории науки книга, полностью посвященная «золотому сечению» и его приложениям. А ее эстетическое значение состоит в том, что иллюстрации к книге сделал сам Леонардо да Винчи! Книга Пачоли состоит из трех частей: в первой части излагаются свойства «золотого сечения», вторая часть посвящена Платоновым телам, третья – приложениям «золотого сечения» в архитектуре. В своей книге Пачоли, апеллируя к «Государству», «Законам», «Тимею» Платона, последовательно выводит 12 различных свойств «золотого сечения». Характеризуя эти свойства, Пачоли пользуется весьма сильными эпитетами: «исключительное», «превосходнейшее», «замечательное», «почти сверхъестественное» и т.п. Раскрывая данную пропорцию в качестве универсального отношения, выражающего и в природе и в искусстве совершенство красоты, он называет ее «божественной» и склонен рассматривать ее как «орудие мышления», «эстетический канон», «как принцип мира и природы».

Книга Луки Пачоли является одним из первых математических сочинений, в котором христианская доктрина о Боге как творце Вселенной получает научное обоснование. Пачоли называет золотое сечение "божественным" и выделяет ряд свойств золотой пропорции, которые, по его мнению, присущи самому Богу:

"Первое заключается в том, что существует только она одна, и невозможно привести примеры пропорций другого рода или хоть сколько-нибудь отличающихся от нее. Эта единственность, согласно с политическим и философским учениями. Есть высочайшее свойство самого Бога. Второе свойство есть свойство святой триединости, а именно, как в божестве одна и та же сущность заключается в трех лицах - отце, сыне и святом духе, так же и одна и та же пропорция этого рода может иметь место только для трех выражений, а для большего и меньшего выражений не существует. Третье свойство заключается в том, что, подобно тому, как Бог не может быть ни определен, ни словом разъяснен, наша пропорция не может быть выражена ни доступным нам числом, ни какой бы то ни было рациональной величиной и остается скрытой и тайной и поэтому математиками названа иррациональной. Четвертое свойство заключается в том, что, подобно тому, как Бог никогда не изменяется и представляет все во всем и все в каждой своей части, и наша пропорция для всякой непрерывной и определенной величины одна и та же, велики или малы эти части, никаким образом не может быть ни изменена, ни по иному воспринята рассудком. К названным свойствам вполне справедливо можно присоединить пятое свойство, заключающееся в том, что, подобно тому, как Бог вызвал к бытию небесную добродетель, иначе называемую пятой субстанцией, а с ее помощью - четыре других простых тела, именно, четыре элемента - землю, воду, воздух и огонь, а с их помощью вызвал к бытию всякую вещь в природе, так и наша божественной пропорция, согласно Платону в его "Тимее", дает формальное бытие самому небу, ибо ему приписывается вид тела, называемого додекаэдром, которое невозможно построить без нашей пропорции".

В этом высказывании Лука Пачоли подчеркивает связь «божественной пропорции» с додекаэдром, который дает «формальное бытие самому небу». Именно эта связь придает додекаэдру особое очарование. Додекаэдр, который «дает формальное бытие самому небу », оказался связанным с «золотой» или «божественной» пропорцией!

7. « Космический кубок » Иоганна Кеплера

Среди патриархов новоевропейской науки нет фигуры более загадочной, чем Иоганн Кеплер (1571-1630): кажется, он соединил две эпохи не только своими творениями, но и самой своей «эллиптической» личностью. С одной стороны, Кеплер — профессиональный астролог, фантазер и фантаст, чей стиль мышления был неприемлем как для творцов классической науки, включая Галилея и Ньютона, так и для ее историков, по крайней мере, историков классической формации. С другой стороны, именно этот — почти средневековый по стилю мышления — звездочет ввел в современную науку ее основные понятия. Современное, то есть механистическое, понимание силы авторы исторического словаря философии возводят к Кеплеру. Он же, оказывается, ввел в обиход слово инерция, отличающее нашу физику от всей прежней, а заодно и физическое понятие энергии, не говоря уже о том, что ему принадлежат первые количественные законы астрономии. Кеплер — учредитель физики неба. Это замечательное словосочетание входит в подзаголовок его основного сочинения: «Новая астрономия, основанная на причинах, или физика неба».

Его первым астрономическим сочинением была небольшая книжечка со следующим названием: «Предвестник космографических исследований, содержащий тайну мироздания относительно чудесных пропорций между небесными кругами и истинных причин, числа и размеров небесных сфер, а также периодических движений, изложенных с помощью пяти правильных тел Иоганном Кеплером из Вюртемберга, математиком из достославной провинции Штирии». Сам он называл эту книгу, опубликованную в 1597 г., «Misterium Cosmographicum» («Тайна космографии»).

Иоганн Кеплер (1571 - 1630)

В этом небольшом сочинении Кеплер попытался раскрыть «тайну космографии». Она основана на Платоновых телах и состоит в следующем: « Земля ( орбита Земли ) есть мера всех орбит. Вокруг нее опишем додекаэдр. Описанная вокруг додекаэдра сфера есть сфера Марса. Вокруг сферы Марса опишем тетраэдр. Описанная вокруг тетраэдра сфера есть сфера Юпитера. Вокруг сферы Юпитера опишем куб. Описанная вокруг тетраэдра сфера есть сфера Сатурна. В сферу Земли вложим икосаэдр. Вписанная в него сфера есть сфера Венеры. В сферу Венеры вложим октаэдр. Вписанная в него сфера есть сфера Меркурия ».

Знаменитый Кеплеров Космический кубок (Рис.3), вправляющий в Платоновы тела хрустальные сферы движения планет Солнечной системы, воплощает эту модель в материи.

Космический кубок позволил Кеплеру прийти к важному выводу, раскрывающему «тайну мироздания»: Вселенная оказалась устроенной на основе единого геометрического принципа, воплощенного в Платоновых телах! Но радость оказалась преждевременной. При всей своей экзальтированности Кеплер был наделен всеми качествами, присущими настоящему ученому. Кеплер понимал, что теория должна согласовываться с результатами наблюдений. Сдерживая восторг, охвативший Кеплера при мысли о своем столь чудесном открытии, Кеплер берется за проверку своей модели.

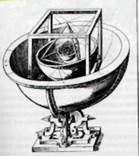
Рисунок 3. « Космический кубок» – Кеплерова модель Солнечной системы

Именно в результате проверки этой модели Кеплер пришел к выдвижению идеи об эллиптическом характере планетных орбит (первый закон Кеплера). Хотя «Космический кубок» оказался ошибочной моделью Солнечной системы, Кеплер никогда не отказывался от «Космического кубка», считая его одним из своих важнейших научных достижений. Уступая настояниям друзей, Кеплер на склоне лет предпринял второе издание своей первой книги «для пользы не только книготорговцев, но и ученых».

В предисловии к новому изданию своей первой книги, подводя итог своим исканиям, Кеплер написал, что все его достижения вдохновлены его первой книгой «Misterium Cosmographicum» с ее Космическим кубком: « Мне самому, в течение вот уже 25 лет работающему над преобразованием астрономии, главы этой книжки не раз освещали путь. Почти все астрономические труды, которые я опубликовал за это время, берут свое начало в той или иной главе моей первой работы …».

«Космический кубок» Кеплера нас интересует, прежде всего, с точки зрения отношения Кеплера к «гипотезе Прокла». Craig Smorinsky в книге [4] обсуждает влияние идей Платона и Евклида на Иоганна Кеплера: « Кеплеровский проект в Mysterium Cosmographicum состоял в том, чтобы дать “ истинные и совершенные причины для чисел, величин и периодических движений небесных орбит ”. Совершенные причины должны основываться на простых принципах математического порядка, который Кеплер нашел в Солнечной системе, используя многочисленные геометрические демонстрации. Общая схема его модели была взята Кеплером из Платоновского Тимея, но математические соотношения для Платоновых тел ( пирамида, куб, октаэдр, додекаэдр, икосаэдр ) были взяты Кеплером из трудов Евклида и Птолемея. При этом Кеплер следовал Проклу в том, что “ главная цель Евклида состояла в том, чтобы построить геометрическую теорию так называемых Платоновых тел ”. Кеплер полностью был очарован Проклом, которого он часто цитирует и называет « пифагорейцем ».

Из этой цитаты мы можем сделать вывод, что Кеплер использовал Платоновы тела для создания своей Космической чаши, но при этом все математические соотношения для Платоновых тел были взяты им из XIII-й книги «Начал», то есть, он объединил в своих исследованиях Космологию Платона с Началами Евклида. При этом он полностью верил в гипотезу Прокла о том, что первичной целью Начал было дать завершенную геометрическую теорию Платоновых тел, которые и были использованы Кеплером в его геометрической модели Солнечной системы (Рис.3).

8. Икосаэдрическая идея Феликса Клейна

Феликс Клейн – выдающийся математик, творчество которого происходило в 19-м и 20-м веках. Он - автор знаменитой «Эрлангенской программы», которая оказала исключительное влияние на развитие геометрии в мире. Клейн был блестящим лектором и популяризатором математики. Как упоминалось, среди пяти Платоновых тел икосаэдр и додекаэдр занимают особое место. В Платоновой космологии икосаэдр символизировал воду, а додекаэдр – гармонию Мироздания. Эти два Платоновых тела непосредственно связаны с пентаклом, а через него – с золотой пропорцией. Додекаэдр и икосаэдр лежат в основе так называемой додекаэдро - икосаэдрической доктрины, которая пронизывает историю всей человеческой культуры, начиная от Пифагора и Платона. И, наверное, нельзя считать случайным, что эта доктрина получила неожиданное развитие в трудах Феликса Клейна (1849 -1925).

В 1884 г. Феликс Клейн опубликовал книгу «Лекции об икосаэдре и решении уравнений пятой степени» [7], посвященную геометрической теории икосаэдра. В первой части книги определено и объяснено место икосаэдра в математике. Согласно Ф. Клейну, ткань математики широко и свободно разбегается листами отдельных теорий. Но есть объекты, в которых сходятся несколько листов, - своеобразные точки ветвления. Их геометрия связывает листы и позволяет охватить общематематический смысл разных теорий. Именно таким математическим объектом, по мнению Клейна, является икосаэдр. Клейн трактует икосаэдр как математический объект, из которого расходятся ветви пяти математических теорий: геометрия, теория Галуа, теория групп, теория инвариантов и дифференциальные уравнения.

Феликс Клейн (1849 - 1925)

Таким образом, главная идея Клейна чрезвычайно проста: « каждый уникальный геометрический объект так или иначе связан со свойствами икосаэдра ».

В чем же состоит значение идей выдающегося математика с точки зрения «гипотезы Прокла» и «теории гармонии»? Прежде всего, в качестве объекта, объединяющего «главные листы» математики выбрано «тело Платона» - икосаэдр, основанный на золотом сечении. Отсюда естественным образом вытекает мысль, что именно золотое сечение и является той главной геометрической идеей, которая, согласно Клейну, может объединить всю математику. Но ведь эта идея есть ни что иное, как своеобразное возвращение к Началам Евклида, в которых Платоновы тела и «золотое сечение» играли определяющую роль.

Современники Клейна (да и современные математики) не сумели по достоинству понять и оценить революционный характер «икосаэдрической» идеи Клейна. А жаль! Развитие науки 20-го века показало гениальность Феликса Клейна, который за сто лет до открытия квазикристаллов и фуллеренов предсказал фундаментальную роль Платоновых тел в развитии современного теоретического естествознания. Как много мыслителей и математиков прошлого (Пачоли, Кеплер, Лобачевский, Клейн) черпали свое вдохновение в Началах Евклида! Жаль, что среди современных математиков приверженцев Евклида не так уж много!

9. Квазикристаллы Дана Шехтмана

Открытие квазикристаллов, сделанное в 1982 г. израильским физиком Даном Шехтманом, является революционным открытием в области кристаллографии, потому что оно экспериментально показало существование кристаллических структур, в которых проявляется икосаэдрическая или пентагональная симметрия, что вступает в противоречие с законами классической кристаллографии. Известный физик Д. Гратиа следующим образом оценивает значение этого открытия для современной науки [8]: « Это понятие привело к расширению кристаллографии, вновь открытые богатства которой мы только начинаем изучать. Его значение в мире минералов можно поставить в один ряд с добавлением понятия иррациональных чисел к рациональным в математике ».

Любопытно приведенное в статье сравнение открытия квазикристаллов, основанных на икосаэдре и додекаэдре, с «добавлением иррациональных чисел... в математике».

Как подчеркивает Гратиа [8], « механическая прочность квазикристаллических сплавов резко возрастает; отсутствие периодичности приводит к замедлению распространения дислокаций по сравнению с обычными металлами … Это свойство имеет большое прикладное значение: применение икосаэдрической фазы позволит получить легкие и очень прочные сплавы внедрением мелких частиц квазикристаллов в алюминиевую матрицу ».

10. Фуллерены ( Нобелевская Премия по химии - 1996)

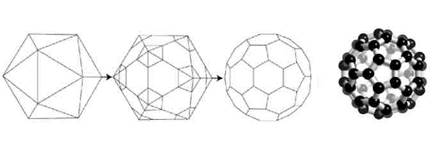
Термином «фуллерены » называют замкнутые молекулы типа С₆₀, С₇₀, С₇₆, С₈₄, в которых все атомы углерода находятся на сферической или сфероидальной поверхности. Центральное место среди фуллеренов занимает молекула С₆₀, которая характеризуется наибольшей симметрией и как следствие наибольшей стабильностью. В этой молекуле, напоминающей покрышку футбольного мяча и имеющую структуру правильного усеченного икосаэдра (Рис. 4), атомы углерода располагаются на сферической поверхности в вершинах 20 правильных шестиугольников и 12 правильных пятиугольников, так что каждый шестиугольник граничит с тремя шестиугольниками и тремя пятиугольниками, а каждый пятиугольник граничит с шестиугольниками.

Впервые они были синтезированы в 1985 учеными Робертом Керлом, Харолдом Крото, Ричардом Смолли (получившими в 1996 г. Нобелевскую премию по химии за это открытие). Фуллерены обладают необычными химическими и физическими свойствами.

Так, при высоком давлении С₆₀ становится твердым, как алмаз. Его молекулы образуют кристаллическую структуру, как бы состоящую из идеально гладких шаров, свободно вращающихся в гранецентрированной кубической решетке. Благодаря этому свойству C₆₀ можно использовать в качестве твердой смазки. Фуллерены обладают также магнитными и сверхпроводящими свойствами.

(а) (б)

Рисунок 4. Усеченный икосаэдр (а) и структура молекулы С₆₀ (б)

Российские ученые А.В. Елецкий и Б.М. Смирнов в своей статье [9] отмечают, что « фуллерены, существование которых было установлено в середине 80- х, а эффективная технология выделения которых была разработана в 1990 г ., в настоящее время стали предметом интенсивных исследований десятков научных групп. За результатами этих исследований пристально наблюдают прикладные фирмы. Поскольку эта модификация углерода преподнесла ученым целый ряд сюрпризов, было бы неразумным обсуждать прогнозы и возможные последствия изучения фуллеренов в ближайшее десятилетие, но следует быть готовым к новым неожиданностям ».

11. Новые подходы в теории элементарных частиц

В последние годы удивительные симметрии Платоновых тел привлекли пристальное внимание физиков-теоретиков, специалистов в теории элементарных частиц [10]. Крупнейший российский специалист по физике высоких энергий академик Л.Б. Окунь писал: « Физиков можно назвать охотниками за симметриями: в некотором смысле они отличаются от остальных людей тем, что отыскивают в природе все более скрытые и все более фундаментальные типы симметрий ».

Статья [10] заканчивается разделом «Вперед, к Платону!», в котором сказано следующее: «Среди Платоновых тел наиболее интересен икосаэдр, и с ним сталкиваются, порой совершенно неожиданно, в самых разных разделах математики. Этот факт должен послужить эвристикой при работе над единой теорией элементарных частиц – ведь в природе наверняка воплощена самая изощренная абстрактная структура. Ее нахождение – прометеева задача наших дней.

Как писал Вернер Гейзенберг, « развитие физики выглядит так, словно в конце концов будут найдены очень простые законы природы – такие, какими их надеялся увидеть Платон ». Не исключено, что эти законы окажутся связанными с правильными многогранниками. Даже когда знания о физической реальности были еще очень скудны, находились мыслители ( Платон, Кеплер ), видевшие в этих фигурах ключ к ее пониманию. Наверное, они составляют, тот арьергард, который всегда впереди ».

Таким образом, главное методологическое значение статьи [10] состоит в том, что она нацеливает физиков-теоретиков на использование Платоновых тел при создании

современной теории элементарных частиц, а это и есть отражение «гармонических идей» древних греков в теоретической физике.

12. Экспериментальное доказательство проявления « золотого сечения » в квантовом мире

В Международном журнале "Science" от 9-го января 2010 опубликована сенсационная информация об экспериментальном обнаружении золотого сечения в квантовом мире. Это - результат многолетних исследований, выполненных в Helmholtz-Zentrum Berlin für Materialien und Energie (HZB) (Германия), Oxford and Bristol Universities и Rutherford Appleton Laboratory (Великобритания). Суть эксперимента состояла в следующем. Ученые сосредоточились на исследовании на наноуровне магнитных свойствах кобальта ниобата. Если воздействовать на этот материал магнитным полем, то удается перевести магнитную цепь в новое квантовое состояние, называемое критическим.

Настраивая систему и искусственно вводя большую квантовую неопределенность, исследователи заметили, что цепочки атомов действуют подобно нано-гитаре, генерирующей колебания различных тонов. При этом первые два тона находятся в совершенном отношении друг к другу. Их частоты находятся в отношении 1,618, известном в искусстве и архитектуре под названием " золотое сечение "! Это открытие дает основания ведущим физикам высказать предположение, что на самом деле в основе квантового, атомного мира лежит совершенный порядок, гармония, основанная на " золотом сечении ". В работе [14] авторы доказали еще одно уникальное свойство: энтропия системы, находящейся в точке «золотого сечения», максимальна! И это является причиной широчайшего распространения «золотого сечения» в структурах природы!

13. Сюрпризы для теоретического естествознания

Нам кажется, что современную науку, в частности физику, химию, биологию, генетику ожидают большие сюрпризы, связанные с « золотым сечением », числами Фибоначчи, Платоновыми и Архимедовыми телами. Особенно с такими телами, как Платоновы икосаэдр и додекаэдр и Архимедов усеченный икосаэдр [12]. Как упоминалось, форму Архимедова усеченного икосаэдра имеет фуллерен С₆₀ (Нобелевская премия 1996 г.), а форму Платонового икосаэдра имеют квазикристаллы Дана Шехтмана. Но не следует забывать, что главной пропорцией Платонового икосаэдра является золотое сечение. И от того, что Архимед осуществил «усечение» Платонового икосаэдра, полученный при этом Архимедов усеченный икосаэдр не перестает быть «золотым», более того, он становится еще более «золотым», так как на его поверхности появляется 12 пентагонов, основанных на золотом сечении. Если к приведенным примерам добавить ботаническое явление филлотаксиса, основанное на гиперболических функциях Фибоначчи и Люка, « золотые » геноматрицы Сергея Петухова, Периодическую систему Менделеева, основанную на обратных числах Фибоначчи (Сергей Якушко), использование пентагональной симметрии и « золотых » спиралей в объектах живой природы, то такое широкое распространение «золотого сечения» в живой и неживой природе дает основание считать доказанным тот факт, что «золотая пропорция» является главной пропорцией мироздания, то есть, некоторым Универсальным Кодом Природы! И этот вывод подтверждается приведенными выше высказываниями Иоганна Кеплера и Алексея Лосева. Но ведь «математика гармонии» [6] предлагает теоретическому естествознанию много новых математических результатов: р - числа Фибоначчи и Люка, золотые р - сечения, лямбда - числа Фибоначчи и « металлические пропорции, гиперболические функции Фибоначчи и Люка, « золотая » фибоначчиева гониометрия. Эти результаты уже начали использоваться в различных разделах теоретического естествознания. Заслуживает внимание сформулированная в [12] новая задача для теоретического естествознания, связанная с поиском новых «гиперболических миров природы», вытекающая из «золотой» фибоначчиевой гониометрии.

14. Заключение: Платоновы тела как уникальные геометрические объекты природы, науки и образования

1. Платоновы тела являются уникальными геометрическими объектами, которым нет аналогов в истории науки. Они были хорошо известны Пифагору и Платону, который на их основе построил оригинальную теорию строения материи. С Платоновыми телами древние греки связывали свое представление о гармонии Мироздания.

2. Согласно «гипотезе Прокла», идеи Платона оказали непосредственное влияние на Евклида, который под влиянием сочинений Платона написал свои Начала, преследуя цель создать завершенную теорию Платоновых тел. Для создания геометрической теории додекаэдра Евклид ввел в Книге II «задачу о делении отрезка в крайнем и среднем отношении» («золотое сечение»), которая в различных модификациях встречается и в остальных Книгах Начал. Таким образом, заслуга Евклида состоит в том, что он связал в единое целое Платоновы тела и «золотое сечение», которые в греческой науке и культуре были главными выразителями гармонии мироздания (Алексей Лосев)

3. Из «гипотезы Прокла» вытекает весьма необычный взгляд на Начала Евклида и развитие математики, начиная с Евклида. Начала Евклида представляют собой не что иное, как первую попытку создать математическую теории гармонии Мироздания, основанную на Платоновых телах и « золотом сечении ». От Евклида начали развиваться два математических направления. Первое из них – это « Классическая математика », которая позаимствовала из Начал аксиоматический подход, теорию чисел и теорию иррациональностей. Второе из них – это « Математики гармонии », которая позаимствовала из Начал Платоновы тела и «золотое сечение».

4. Особенно ярко связь Платоновых тел и «золотого сечения» подчеркивается в книге выдающегося итальянского математика эпохи Возрождения Луки Пачоли «Божественная пропорция» (1509 г.), которая была написана под непосредственным влиянием и даже участием Леонардо да Винчи. По мнению Пачоли, «наша божественной пропорция, согласно Платону в его "Тимее", дает формальное бытие самому небу, ибо ему приписывается вид тела, называемого додекаэдром, которое невозможно построить без нашей пропорции".

5. Платоновы тела вдохновили Иоганна Кеплера на создание «Космического кубка» -оригинальной модели Солнечной системы, описанной в его первой книге «Misterium Cosmographicum». Эта книга оказала основополагающее влияние на все последующие научные открытия Кеплера. По мнению Кеплера, « главы этой книжки не раз освещали путь. Почти все астрономические труды, которые я опубликовал за это время, берут свое начало в той или иной главе моей первой работы …».

6. Платоновы тела вдохновили также выдающегося математика Феликса Клейна на написание книги «Лекции об икосаэдре и решении уравнений пятой степени» [7]. В этой книге он выдвигает следующую необычную мысль. Согласно Ф. Клейну, ткань математики широко и свободно разбегается листами отдельных теорий. Но есть объекты, в которых сходятся несколько листов, - своеобразные точки ветвления. Их геометрия связывает листы и позволяет охватить общематематический смысл разных теорий. Именно таким математическим объектом, по мнению Клейна, является икосаэдр. Клейн трактует икосаэдр как математический объект, из которого расходятся ветви пяти математических теорий: геометрия, теория Галуа, теория групп, теория инвариантов и дифференциальные уравнения. Достойно удивления и сожаления, что идеи Клейна до сих пор не получили должного отражения и развития в современной математике.

7. Платоновы тела обладают исключительными симметрическими свойствами. Именно их симметрия, в частности, группы симметрий додекаэдра и икосаэдра, стали причиной большого интереса, который возник к Платоновым телам в современной теории элементарных частиц.

8. Последняя четверть 20-го века стала триумфальным периодом для Платоновых тел. Именно в этот период были сделаны два научных открытия, связанные с Платоновыми телами. Первое из них – это открытие квазикристаллов, основанное на икосаэдрической симметрии, и опровергающее законы классической кристаллографии. Второе – это открытие фуллеренов, основанных на Архимедовом усеченном икосаэдре. Это выдающееся открытие в области химии удостоено в 1996 г. Нобелевской Премии. Эти два открытия, затрагивающие основания теоретического естествознания, больше, чем другие научные открытия, подчеркивают гениальность Пифагора, Платона и Евклида, которые два с половиной тысячелетия тому предсказали выдающуюся роль Платоновых тел и «золотого сечения» в теоретическом изучении Природы. Экспериментальное обнаружение « золотого сечения » в квантовом мире (2010 г.) является физическим открытием, которое подтверждает фундаментальную роль «золотого сечения» в современной теоретической физике!

9. Платоновы тела и «золотое сечение» представляют огромный интерес для математического образования. Новый взгляд на «Начала» Евклида, вытекающий из гипотезы Прокла, требует переосмысливания программы математического образования. В этой программе Платоновы тела и «золотое сечение» должны занимать такое же место, как «теорема Пифагора» и тригонометрия. С точки зрения математического образования особую роль может сыграть «Математика гармонии» [6], которая должна быть введена в учебные планы средних школ, колледжей и университетов.

10. Из вышеизложенного, а также из анализа, проведенного в работе [12], можно сделать вывод о том, что роль Платоновых тел и « золотого сечения » в развитии математики, теоретического естествознания, компьютерной науки, экономики, образования до конца еще не осознана и что по своему влиянию на развитие математики и науки в целом их можно поставить в один ряд не только с « теоремой Пифагора » ( Кеплер ), но даже с натуральными и иррациональными числами. Использование Платоновых тел и « золотого сечения » в современном теоретическом естествознании настолько масштабно, что можно даже говорить о « Золотой » Научной Революции! « Вперед к Платону !» -таким должен стать девиз современной науки!

Литература:

1. Сороко Э.М. Структурная гармония систем. Минск: Наука и техника, 1984.

2. Charles H. Kann. Pythagoras and Pythagoreans. A Brief History. Hackett Publishing Co, Inc., 2001.

3. Leonid Zhmud. The origin of the History of Science in Classical Antiquity. Published by Walter de Gruyter, 2006.

4. Craig Smorinsky. History of Mathematics. A Supplement. Springer, 2008

5. Колмогоров А.Н. Математика в ее историческом развитии. Москва: Наука, 1991.

6. Alexey Stakhov. The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science. World Scientific, 2009.

7. Клейн Ф. Лекции об икосаэдре и решении уравнен6ий пятой степени (пер. с нем.). Москва: Наука, 1989.

8. Гратиа Д. Квазикристаллы. Успехи физических наук, 1988, том 156, вып. 2.

9. Елецкий А.В., Смирнов Б.М. Фуллерены. Успехи физических наук, 1993, том 163, №2.

10. Верховский Л.И. Платоновы тела и элементарные частицы. Химия и жизнь, 2006, №6.

11. Владимиров Ю.С. Кварковый икосаэдр, заряды и угол Вайнберга. Труды международной конференции «Проблемы Гармонии, Симметрии и Золотого Сечения в Природе, Науке и Искусстве», Винница – 2003.

12. Стахов А.П. Эстетика математики гармонии как «золотой» парадигмы современной науки. Доклад на пленарном заседании 1-го Международного Конгресса по Математике Гармонии (Одесский национальный университет, 8-10 октября 2010) https://docs.google.com/fileview?id=0B5BajO1r9mlMNjQzNDkwZDYtYTlmMS00Yz N jLTgwNTctYjU0NDMyNTI3MjQ2&hl=en&authkey=CI_AkRc

13. Владимиров В.Л. Ряды Фибоначчи, Люка и степеней золотой константы – частные случаи дивизорных возвратных последовательностей. Доклад на Международном Конгрессе по Математике Гармонии (Одесса, 8-10 октября 2010). http://www.goldensectionclub.net/home/congress/speeches.

14. Владимиров В.Л., Стахов А.П. Энтропия золотого сечения (раскрыта еще одна тайна золотого сечения) // «Академия Тринитаризма», М., Эл № 77-6567, публ.16523, 22.05.2011 http://www.trinitas.ru/rus/doc/0232/009a/02321199.htm

15. Владимиров В.Л., Стахов А.П. Энтропийный анализ известных рекурсий. Международный Клуб Золотого Сечения. Публикация от 16.3.2011 http://www.goldensectionclub.net/publications/vladimirov/vladimirov - articles/vladimirov002

16. Владимиров В.Л., Стахов А.П. Гиперболические уравнения Золотого Сечения. // «Академия Тринитаризма», М., Эл № 77-6567, публ.16548, 05.06.2011 http://www.trinitas.ru/rus/doc/0232/009a/02321200.htm.