
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение матричных игр методами линейного программирования
Для парных игр разработан достаточно простой аналитический метод решения, базирующийся на основных положениях линейного программирования с привлечением принципов двойственности ЗЛП.
Рассмотрим игру m×n, определяемую матрицей А. Предположим, что ее решение возможно только в смешанных стратегиях. Тогда, согласно теореме 3, для оптимальной стратегии первого игрока 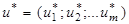 и цены игры v выполняется неравенство
и цены игры v выполняется неравенство
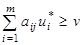 , при j=1…n.
, при j=1…n.
Предположим, что v>0. Теперь разделим левую и правую части этого неравенства на v и получим
 , при j=1…n.
, при j=1…n.
Положим 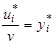 . Тогда
. Тогда
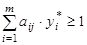 , при j=1…n, yi* ≥ 0.
, при j=1…n, yi* ≥ 0.
Используя введенное обозначение, перепишем дополнительное условие 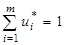 в виде:
в виде:
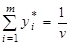 .
.
Так как первый игрок стремится получить максимальный выигрыш, то он должен обеспечить минимум величины 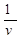 . С учетом этого, определение оптимальной смешанной стратегии первого игрока сводится к нахождению минимального значения функции
. С учетом этого, определение оптимальной смешанной стратегии первого игрока сводится к нахождению минимального значения функции
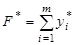 → min
→ min
при условиях 
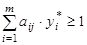 , при j=1…n,
, при j=1…n,
yi* ≥ 0.
Аналогичные рассуждения показывают, что определение оптимальной стратегии второго игрока сводится к нахождению максимального значения функции
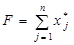 → max
→ max
при условиях 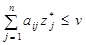
или 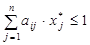 , i=1…m
, i=1…m
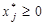 ,
,
где 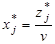 .
.
Таким образом, чтобы найти решение данной игры, определяемой матрицей А, нужно составить следующую двойственную пару ЗЛП и найти их решение
- прямая задача: найти максимальное значение функции
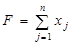 → max
→ max
при условиях 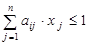 , i=1…m
, i=1…m
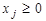 ,
,
- двойственная задача: найти минимальное значение функции
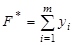 → min
→ min
при условиях 
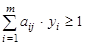 , j=1…n,
, j=1…n,
 .
.
Используя решение этой двойственной пары, получаем формулы для расчета смешанных стратегий и цены игры:
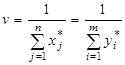 ;
; 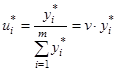 ;
; 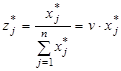 ; (27)
; (27)
i=1…m; j=1…n.
Итак, процесс нахождения решения игры с использованием методов линейного программирования, включает следующие этапы:
1) составляют пару двойственных задач линейного программирования, эквивалентных данной матричной игре;
2) определяют оптимальные планы двойственных задач;
3) используя формулы (27), находят решение игры.
Таким образом, для всякой матричной игры всегда можно записать симметричную пару двойственных задач. Справедливо и обратное: для всякой симметричной пары двойственных задач можно записать матричную игру. Схема этого построения следующая.
Пусть задана симметричная пара двойственных задач:
прямая задача:  → max;
→ max; 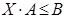 ;
; 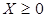 ;
;
двойственная задача: 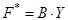 → min;
→ min; 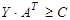 ;
; 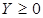 .
.
Этой симметричной паре двойственных задач можно поставить в соответствие игру, определяемую матрицей:
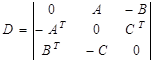 ,
,
где индекс (Т) означает операцию транспонирования.
З а д а ч а 21. Построить игру, определяемую следующей парой двойственных задач:
прямая задача: 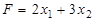 → max,
→ max,
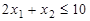 ,
,
 ,
,
Х ≥ 0;
двойственная задача: 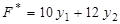 → min,
→ min,
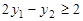 ,
,
 ,
,
Y ≥ 0.
Р е ш е н и е. Запишем все элементы будущей матрицы игры. Они следующие:
- матрица коэффициентов в прямой задаче 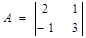 ;
;
- матрица коэффициентов в двойственной задаче 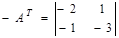 ;
;
- вектор-столбец свободных членов в
ограничениях прямой задачи 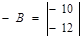 ;
;
- транспонированный столбец 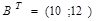 ,
,
- вектор-строка свободных членов 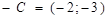 ,
,
- транспонированная вектор-строка 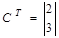 .
.
Следовательно, исходной симметричной паре двойственных задач можно поставить в соответствие матричную игру, определяемую матрицей:
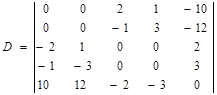 .
.
Важно заметить, что любая игра имеет смешанную оптимальную стратегию, но не каждая ЗЛП имеет решение.
В качестве примера рассмотрим задачу 19, видоизменив матрицу игры.
З а д а ч а 22. Найти решение игры, заданное матрицей
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 |
Р е ш е н и е. Прежде всего определим максимин и минимакс. Для этого напишем вектора:
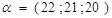 ;
; 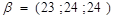 .
.
Следовательно, 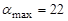 ,
, 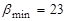 . Так как седловой точки в этой задаче нет, будем искать решение в смешанных стратегиях. Составим двойственную пару ЗЛП:
. Так как седловой точки в этой задаче нет, будем искать решение в смешанных стратегиях. Составим двойственную пару ЗЛП:
- прямая задача: найти максимум функции 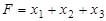
при ограничениях 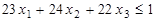 ,
,
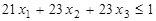 ,
,
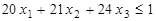 ,
,
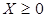 ;
;
- двойственная задача: найти минимум функции 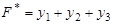
при ограничениях 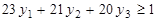 ,
,
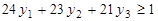 ,
,
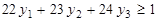 ,
,
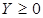 .
.
Очевидно, из двух задач проще решить прямую задачу, так как у нее ограничения состоят из неравенств типа “≤ ”, а в таком случае очень просто ограничения переписать в виде равенств с добавлением еще трех переменных х4, х5, х6 и получением трех единичных векторов Р4, Р5, Р6.
Решение этой ЗЛП выполняется в три итерационных шага и имеет вид:
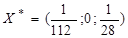 ;
;  .
.
Цену игры определим из (27). Например,
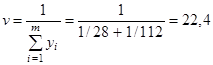 .
.
Тогда смешанная стратегия для первого игрока определится так:
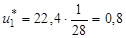 ,
, 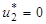 ,
,  .
.
Для второго игрока смешанная стратегия будет составлять:
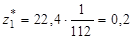 ,
,  ,
, 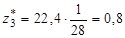 .
.
Окончательный ответ: цена игры равна 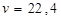 ; игроки имеют смешанные стратегии
; игроки имеют смешанные стратегии 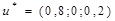 .
. 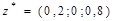 .
.
Решение задачи 21 показывает, как незначительное изменение в структуре матрицы игры может привести к существенному изменению содержания и объема решения задачи.
Date: 2015-09-18; view: 688; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |