Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Подпространства линейных пространств
|
|
1о. Определение подпространства и линейной оболочки
Определение 1. Непустое подмножество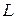 
векторного пространства 
над множеством действительных чисел R называется линейным подпространством (или просто подпространством) линейного пространства , если выполняются следующие свойства:
1. 
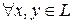, их сумма 
.
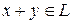2. 
, 
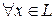R, имеем: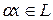 
.
Лемма 1. Подпространство 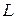векторного пространства само является векторным пространством.
Доказательство. Покажем, что 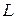удовлетворяет аксиомам сложения из определения линейного пространства. Так как ассоциативность и коммутативность выполняются для любых элементов , то эти свойства выполняются и для 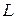. Осталось проверить, что 
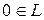и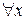 
, его противоположный элемент 
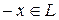. Действительно, так как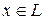 
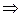
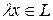
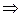при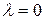 
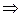
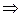
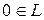. Аналогично, 
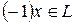и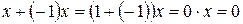 
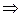
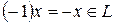и является противоположным к 
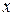. Аксиомы умножения на скаляр справедливы, так как они справедливы для любых элементов .
Примеры:
1) 
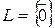и 
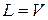подпространства линейного пространства : они называются несобственными подпространствами.
2) Множество симметричных (квадратных) матриц порядка n является подпространством в пространстве всех квадратных матриц порядка n.
Рассмотрим множество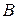 
векторов пространства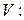 
.
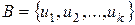Определение 2. Линейной оболочкой множества 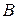(линейной оболочкой 
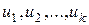) будем называть совокупность всех линейных комбинаций этих элементов, т.е. множество элементов вида
,
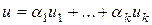где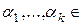 
R – произвольные вещественные числа.
Обозначение.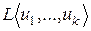 
– линейная оболочка 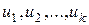. Множество 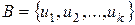называется множеством или системой образующих для .
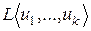Лемма 2. Любая линейная оболочка является подпространством основного линейного пространства , причем линейная оболочка является наименьшим подпространством, содержащим .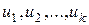
Доказательство. То, что 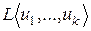– подпространство, следует из того, что для 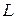выполняются аксиомы 1о, 2о Определения 1. Так как это подпространство содержит 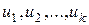и, с другой стороны, любое другое подпространство, содержащее 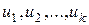, будет содержать их линейные оболочки и значит содержит 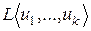, т.е. 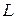– подмножество такого множества.
Пример. Если рассмотреть R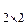 
, и 
, 
, 
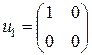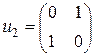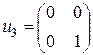,, то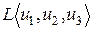 
является подпространством симметричных матриц порядка 2.
Date: 2015-09-03; view: 405; Нарушение авторских прав