Критическая скорость, критическое сечение и критические параметры

Понятие критической скорости удобно ввести, рассматривая процесс истечения газа из резервуара через сопло в атмосферу, хотя эта величина применяется в самых разнообразных задачах, не обязательно связанных с процессом истечения. На рис.14 внизу изображены кривые изменения скорости потока, температуры и местной скорости звука по длине сопла, через которое движется газ. Это течение является энергоизолированным, поэтому связь между скоростью и температурой выражается с помощью уравнения энергии в форме (2.19)[3]. По мере нарастания скорости по длине сопла, температура, как это следует из уравнения энергии (2.19), а следовательно, и скорость звука (2.37) уменьшаются. Таким образом; в различных сечениях одного и того же потока скорость звука получается разной. В начале сопла скорость потока ниже скорости звука, в конце — превышает ее. Где-то в средней части сопла существует сечение, в котором скорость потока равна местной скорости звука. Это сечение называется критическим, а параметры потока в нем — критическими параметрами. Ниже будет показано, что если газ движется без трения и без обмена энергией с внешней средой, то критическое сечение совпадает с самым узким местом канала — горлом сопла.

Можно так сформулировать понятие критической скорости: критической скоростью называется такая скорость течения газа, которая равна местной скорости звука. Можно дать и другую формулировку, принимая во внимание то обстоятельство, что в точке пересечения кривых на рис.14 проходит как кривая скорости потока, так и кривая скорости звука, а именно: критической скоростью звука называется такое значение местной скорости звука, которое равно скорости потока газа в данном месте. Как видим, в обоих случаях численное значение получится одним и тем же, поэтому безразлично, как именовать эту величину — критической скоростью или критической скоростью звука — и как обозначать ее: w_кр или а_кр. Более распространено название «критическая скорость» и обозначение а_кр.

Рассчитать критическую скорость можно по формуле

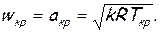(2.42)

где Т_кр — температура газа в критическом сечении. Последняя легко определяется с помощью уравнения энергии (2.19), левая часть которого записывается для сечения внутри резервуара (см. рис. 14), где w=0, Т=Т*, а правая часть — для критического сечения, в котором w_кр = а_кр, Т=Т_кр, а именно:

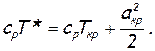
Заменив здесь 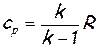и а_{к р} по формуле (2.42), получим после небольших преобразований

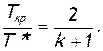(2.43)

Эта величина называется критическим отношением температур. Попутно запишем формулы для критического отношения давлений и для критического отношения плотностей. Так как процесс течения газа через сопло идеальный, то связь между давлениями, плотностями и температурами устанавливается уравнением изоэнтропы (2.33). Тогда

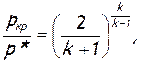(2.44)

(2.45)

Для воздуха эти соотношения имеют следующие значения:

Определив из соотношения (2.43) температуру Т_кр и подставив ее значение в формулу (2.42), приходим к наиболее удобной формуле для расчета критической скорости

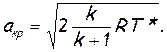(2.46)

Для воздуха .

Следовательно, 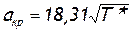м/сек. (2.47)

& [1] с.20…24. [3] с.40…42. [4] с.56..58. [5] с.415…418; с.421…424.

& [6] с.135…139. [7] с.51…56. [8] с.193.

31. Безразмерные скорости: относительная и приведенная скорости, число Маха

Обычно скорость движения измеряется в метрах в секунду, километрах в час или каких-нибудь других единицах, имеющих размерность длина/время. Если же за единицу измерения скорости принять какую-либо из характерных скоростей, например скорость звука, то результат измерения будет выражаться безразмерным числом.

Наиболее распространены три безразмерные скорости: число М, приведенная скорость λ и приведенная (относительная) скорость Λ. Приведенные скорости иначе называют коэффициентами скорости.

Числом М называется отношение скорости потока к местной скорости звука

M = w / a. (2.50)

Впервые эта величина была использована в трудах профессора Петербургской артиллерийской академии Н.В.Маиевского (1868), затем этим отношением пользовался австрийский физик Э.Мах (1887). В связи с этим в советской технической литературе отношение _ часто называют числом Маиевского, в немецкой — числом Маха. Иногда в английской литературе эту величину называют числом Бэрстоу.

Приведенной скоростью, или коэффициентом скорости λ называется отношение скорости потока к критической скорости

λ = w / a_кр. (2.51)

Числом Λ или относительной скоростью называется отношение скорости потока к максимальной скорости течения газа

Λ = w / w_max. (2.52)

Заметим, что величиной w²/w²_max = Λ² пользовался академик С.А. Чаплыгин еще в первых работах по газовой динамике. Поэтому ее иногда называют числом Чаплыгина.

Численное значение безразмерных скоростей может изменяться в следующем диапазоне:

число М от 0 до ∞

число λ от 0 до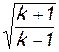

число Λ от 0 до 1,

так как скорость потока может изменяться от 0 до w_mах, а местная скорость звука в том сечении, где w=w_max, равна нулю (потому что температура равна нулю).

Связь между приведенными скоростями λ и Λ устанавливается следующим путем:

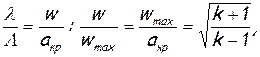
следовательно,

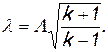(2.53)

Для установления зависимости между приведенной скоростью и числом М возьмем отношение их квадратов

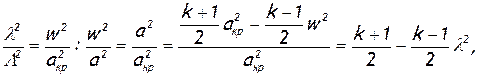
откуда

(2.54)

или

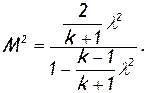(2.55)

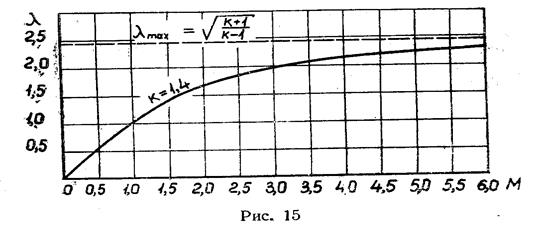
График зависимости приведенной скорости от числа М изображен на рис.15. Из графика видно, что значения М и λ численно совпадают при М=1 и М=0. Когда М−›∞, то приведенная скорость λ стремится ко вполне определенному пределу

Это значение легко получить, устремив число М к бесконечности. Тогда w стремится к максимальной скорости и λ — к величине w_max / a_кр, которая равна 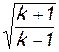(см. формулу (2.48)). Последняя является наибольшей из всех возможных величин λ и называется максимальной приведенной скоростью λ _мах. Для воздуха (k = 1,4) λ_max = 2,449.

Числа М, λ и Λ являются критериями подобия для сжимаемой жидкости. Так например, если в двух геометрически подобных каналах числа М на входе будут одинаковы, то отношения скоростей, давлений, температур, плотностей в двух сечениях одного канала будут равны соответствующим отношениям в двух сходственных сечениях другого канала.

Поскольку число М связано с приведенными скоростями λ и Λ однозначными зависимостями, то, вместо того, чтобы устанавливать одинаковые числа М на входе в каналы, можно установить одинаковые числа λ или одинаковые числа Λ. В этом случае подобие потоков также будет соблюдаться.

& [1] с.20…24. [3] с.42…47. [4] с.56..60. [5] с.416…418.

& [6] с.135…139. [7] с.49…51. [8] с.193..195.

Date: 2015-09-03; view: 10994; Нарушение авторских прав