Геометрическое воздействие. Уравнение Гюгонио

На практике мы наиболее часто сталкиваемся с геометрическим воздействием на течение жидкости, когда имеет место только изменение площади проходного сечения канала по длине. Это прежде всего сопла и диффузоры реактивных двигателей, компрессоров и турбин. Изучение этих течений как одномерных при условии отсутствия других воздействий является наиболее простым для анализа.

Продифференцировав уравнение неразрывности (расхода) для изолированного одномерного течения (для элементарной струйки)

m=ρWF = Const,

где m – массовый расход, ρ – плотность, W – скорость жидкости, а F – площадь проходного сечения канала;

и разделив почленно на m=ρWF, получим дифференциальное уравнение неразрывности

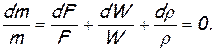
Исключим из этого уравнения член, учитывающий изменение плотности. С этой целью преобразуем уравнение Бернулли для изолированного течения (для элементарной струйки):

,

с учетом выражения для скорости звука

a²=dp/dρ

или

.

Подставив последнее выражение для плотности в дифференциальное уравнение неразрывности, получим частный случай уравнения обращения воздействия для случая геометрического воздействия на течение жидкости – уравнение Гюгонио:

,

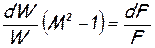которое показывает, что

дозвуковой поток (при M<1)

-ускоряется (dW>0) в сужающихся каналах (dF<0)

и тормозится (dW<0) в расширяющихся каналах (dF>0),

а сверхзвуковой поток (при M>1) наоборот

- ускоряется (dW>0) в расширяющихся каналах (dF>0)

и тормозится (dW<0) в сужающихся каналах (dF<0).

Очевидно также, что если площадь канала остается постоянной (dF=0), то и в дозвуковом и в сверхзвуковом потоке скорость должна сохраняться неизменной по длине канала (dW=0).

Для того, чтобы разогнать дозвуковой поток до сверхзвуковой скорости в трубе переменного сечения, необходимо сначала суживать трубу, а затем расширять.

Переход через скорость звука (M=1) может произойти только в минимальном сечении трубы, так как при M=1 только при dF=0 скорость W может иметь конечное значение (не становится бесконечно большой). Такие трубы или каналы называются соплами Лаваля (по имени шведского инженера Лаваля впервые применившего сопла в паровых турбинах для получения сверхзвуковых скоростей).

Date: 2015-09-03; view: 1653; Нарушение авторских прав