Доказательство

В силу теоремы 1 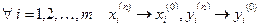. Тогда по свойствам числовых последовательностей 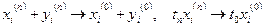, 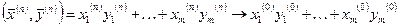. Последнее соотношение выражает непрерывность скалярного произведения. Из первых двух соотношений на основании теоремы 1 приходим к выводу . Теорема 4 доказана.

§4. Предел функции m переменных

Пусть числовая функция f определена на множестве . Будем использовать обозначение 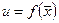или .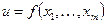

Пусть точка 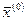- предельная точка множества X.

Определение 1.(предела функции по Гейне)

Число a называется пределом функции f в точке 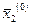, если для любой сходящейся к точке 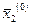последовательности 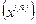точек множества X, все элементы которой отличны от 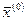, числовая последовательность значений функции 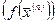сходится к числу a.

Определение 1*.(предела функции в точке по Коши)

Число a называется пределом функции f в точке 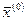, если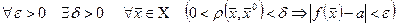

Для обозначения предела используется следующая символика:

.

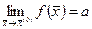Доказательство эквивалентности определения 1 и 1* проводится точно так же, как и для функции одной переменной.

Введем понятие предела функции f при 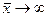. Для этого положим, что множество X для любого 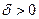имеет хотя бы один элемент, лежащий вне шара радиуса 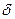с центром в точке 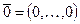. Ограничимся определением по Коши.

Определение 2.

Число a называется пределом функции f при 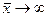, если .

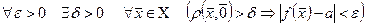Так же, как и для функции одной переменной, доказывается теорема 1.

Теорема 1. Если 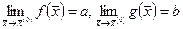, то

,

,

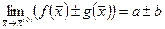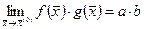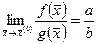при дополнительном требовании, что 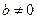и функция g в ноль не обращается.

Определение 3.

Будем говорить, что функция f удовлетворяет условию Коши в точке 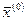(соответственно при 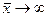), если

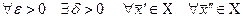
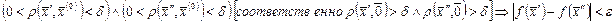
Date: 2015-09-03; view: 333; Нарушение авторских прав