Пространства функционалов. Сопряжённые операторы

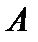
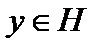Пусть непрерывный линейный оператор, действующий в гильбертовом пространстве . Зафиксировав , рассмотрим скалярное произведение 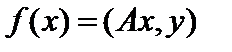как функционал относительно переменной 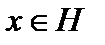. Оператор 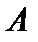линеен, то есть функционал линеен по переменной 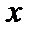и ограничен, так как . По теореме Рисса о виде непрерывного линейного функционала, заданного на 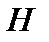пространстве, имеет место равенство . Здесь элемент однозначно определен элементом 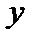и оператором , то есть определяет некий оператор как .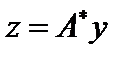

Определение. Оператор 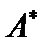называют сопряженным к оператору . Другими словами, оператор называется сопряжённым к 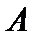, если 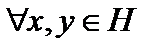скалярное произведение . Оператор 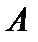называется самосопряжённым, если , унитарным, если , и нормальным, если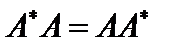

Рассмотрим пространство 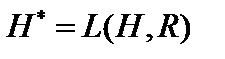непрерывных линейных функционалов, заданных на гильбертовом пространстве . Это пространство называют сопряженным к гильбертову пространству .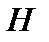

Определение. Последовательность в гильбертовом пространстве 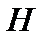называется слабо сходящейсяк элементу 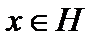, если 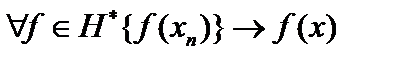, то есть .

Комментарий. 1. Значение функционала 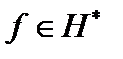в точке 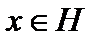обозначается как скалярное произведение 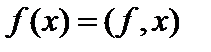. Тогда сопряжённый оператор можно определить, как . Но это просто обозначение, маскирующее отсутствие в 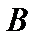- пространствах скалярного произведения. Даже в конечномерном случае, когда 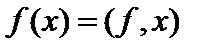имеет смысл скалярного произведения, вектор контравариантен, а вектор 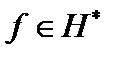- это вектор коэффициентов преобразований, он ковариантен. Эти векторы находятся в разных пространствах и по-разному преобразуются при смене системы координат.

2.Напомним, что сходимость по норме пространства носителей это обычная сходимость, когда 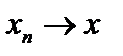, то есть 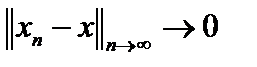. Её называют сильной. Если носителем является пространство , то такая сходимость называется равномерной сходимостью. В пространстве непрерывных линейных операторов сходимость всегда называется равномерной сходимостью. Если же , то такая сходимость в пространстве называется поточечной или сильной. Используя понятие сопряжённого пространства, в пространстве носителей можно ввести и другой тип сходимости, то есть другую топологию, а именно, слабую сходимость. Но это, по сути, поточечная сходимость. Сильная сходимость влечёт слабую, так как , и при 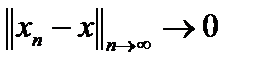, то есть сильно, 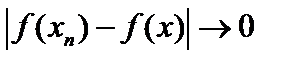, то есть слабо. Обратное, вообще говоря, неверно. Пусть 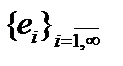- базис в - пространстве и функционал . Из теоремы Рисса об общем виде функционала в гильбертовом пространстве, . Ясно, что последовательность 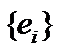не стремится к нулю, она даже не фундаментальна, так как . Но по свойству коэффициентов Фурье последовательность , то есть слабо.

Пример. Рассмотрим оператор Фредгольма 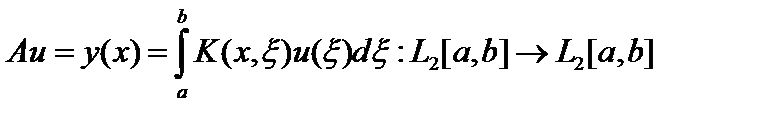, где функция 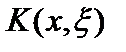, то есть ядро оператора 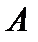удовлетворяет условию Гильберта-Шмидта 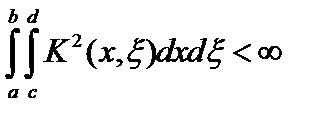. Тогда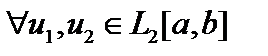

.

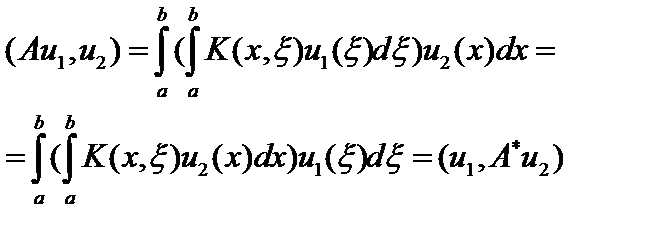Но с другой стороны,

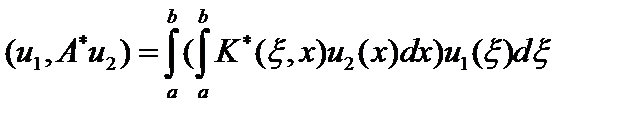, то есть .

Итак, оператор 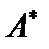также является оператором Фредгольма с ядром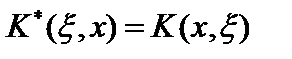 . Если 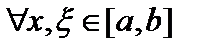,то ядро 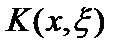называется симметрическим. В этом случае, при , интегральный оператор является самосопряженным. Если ядро интегрального оператора не симметрическое, то оператор не самосопряжён.

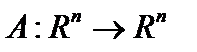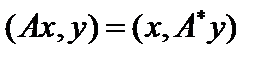Пример. Рассмотрим в пространстве оператор , то есть , причём . По определению , то есть 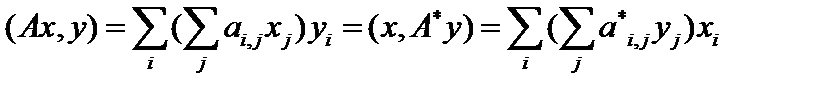. Поменяв местами индексы, сразу получим, что , то есть переход к сопряженному оператору в действительном 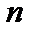-мерном пространстве означает транспонирование матрицы этого оператора.

Пример. К оператору , действующему по формуле , вычислить сопряженный.

Оператор А является линейным и ограниченным, отображающим гильбертово пространство в себя. Для построения сопряженного оператора воспользуемся определением:

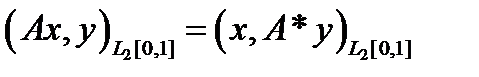для .

Тогда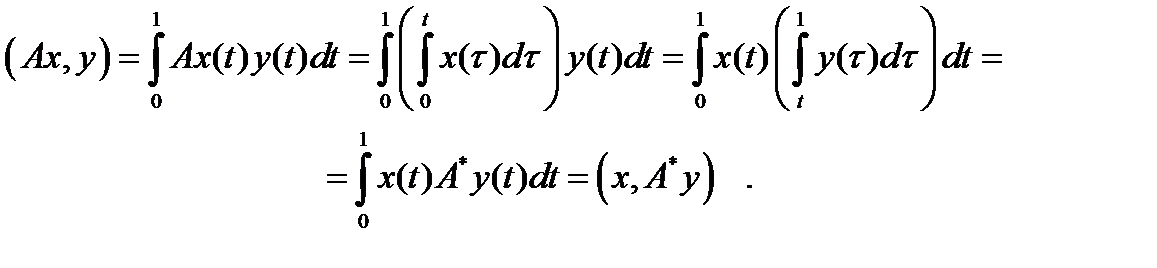

Следовательно, сопряженный оператор определяется соотношением . Видно, что оператор А не является самосопряженным.

Пример. Линейный функционал в пространствах 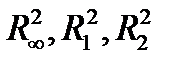в точках (1,2) и (3,4) равен 5 и 6 соответственно. Найти его значение в точке (7,8) и норму.

Пример. Значение линейного функционала в 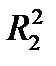в точке (1,1) равно 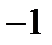, а его норма равна . Найти его значение в точке (7,8). Линейный функционал, заданный на плоскости, имеет вид 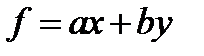, то есть это плоскость, проходящая через начало координат. Его норма – это максимальное значение этой функции на единичном шаре в 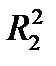. Таким образом, имеем симметрическую СЛАУ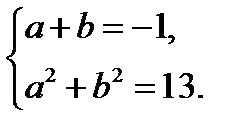

Пример. Норма функционала 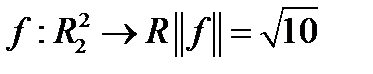, а его значение в точке 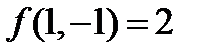. Найти его значение в точке .

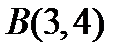По теореме Рисса об общем виде линейного непрерывного функционала в гильбертовом пространстве, для всякого непрерывного линейного функционала 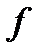существует единственный вектор такой, что 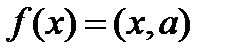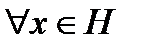, причем . Тогда . Таким образом, имеем систему

Комментарий. Из геометрического смысла понятия нормы видно, что общий вид линейного функционала в пространствах 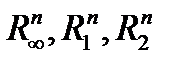задаётся формулой 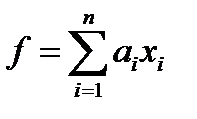, где . Нормы же их определяются выражениями .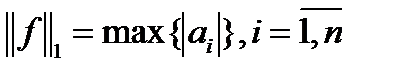

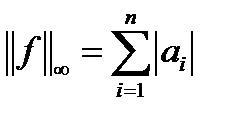
Date: 2015-09-03; view: 719; Нарушение авторских прав