Определение линейного пространства

Лекция 13

ЛИНЕЙНОЕ ПРОСТРАНСТВО

Определение линейного пространства

Определение. Множество R,состоящее из элементов 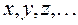, для которых определена операция сравнения, называется линейным пространством, если

(1). Каждой паре элементов 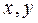этого множества поставлен в соответствие третий элемент этого же множества, называемый их суммой и обозначаемый , таким образом, что выполнены аксиомы

а) ;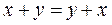

б) ;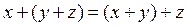

в) существует нулевой элемент 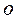, такой, что для любого имеет место ;

г) для каждого существует противоположный элемент 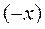, такой, что .

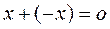(2). Для любого элемента 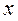и любого числа существует такой принадлежащий R элемент, обозначаемый и называемый произведением числа на элемент, что выполнены аксиомы:

а) ;

б) .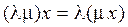

(3). Для операций сложения элементов и умножения элемента на число выполнены аксиомы дистрибутивности:

а) ;

б) 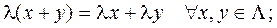и для любых чисел .

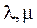Замечание. Первая группа аксиом равносильна требованию, чтобы R являлось абелевой группой относительно операции сложения.

Линейным пространством является:

(1). Множество всех векторов на плоскости.

(2). Множество всех векторов в пространстве.

(3). Множество всех n -компонентных столбцов.

(4). Множество всех многочленов степени не выше, чем n.

(5). Множество всех матриц размера .

(6). C [ a, b ] – множество всех функций, непрерывных на [ a, b ].

(7). Множество всех решений однородной системы m линейных уравнений с n неизвестными

Теорема 13.1 Линейное пространство имеет единственный нулевой элемент.

Доказательство.

Пусть существуют два различных нулевых элемента 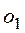и . Тогда, согласно аксиоме (1) пункт (в) из определения линейного пространства, будут справедливы равенства

и .

Откуда в силу коммутативности операции сложения получаем .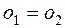

Теорема доказана.

Теорема 13.2 Для каждого элемента x линейного пространства имеет место равенство .

Доказательство.

Из аксиоматики линейного пространства имеем

Прибавляя к обеим частям равенства 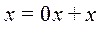элемент y, противоположный элементу x, получаем, что .

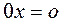Теорема доказана.

Теорема 13.3 Для каждого элемента линейного пространства существует единственный противоположный элемент.

Доказательство.

Пусть для элемента x существуют два различных противоположных элемента 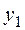и . Тогда, согласно аксиоме (1) пункт (г) линейного пространства, будут справедливы равенства и 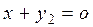. Прибавим к обеим частям первого равенства элемент 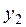, получим

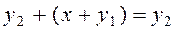
в силу ассоциативности операции сложения и второго равенства. Но, с другой стороны,

.

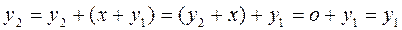То есть .

Теорема доказана.

Теорема 13.4 Для каждого 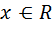противоположным элементом служит элемент .

Доказательство.

Из аксиоматики линейного пространства и в силу теорем 13.2–13.3 имеем

.

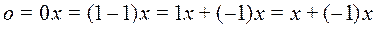Это равенство и означает, что противоположный к x элемент имеет вид .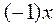

Теорема доказана.

Date: 2015-09-03; view: 327; Нарушение авторских прав