
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Высших порядков
Пусть дана функция 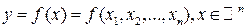 . Определенные ранее частные производные
. Определенные ранее частные производные  называют также частными производными первого порядка.
называют также частными производными первого порядка.
Пусть теперь для 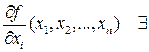 -ет частная производная по
-ет частная производная по 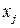 в точке
в точке  . Тогда
. Тогда 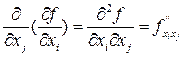 называют частными производными второго порядка.
называют частными производными второго порядка.
Аналогично. Частной производной порядка 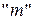 называется частная производная (по любой переменной
называется частная производная (по любой переменной 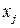 ) от частной производной порядка
) от частной производной порядка 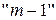 .
.
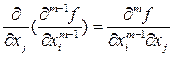
Частная производная, полученная дифференцированием по различным переменным, называется смешанной.
Например:  и т.д.
и т.д.
Пусть 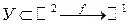 , т.е.
, т.е.  - определена в некоторой области E.
- определена в некоторой области E.  - также являются функциями двух переменных и определены в области E или ее части.
- также являются функциями двух переменных и определены в области E или ее части.
Частные производные по x и y от функций  в точке (x,y) если они существуют, называются частными производными второго порядка в точке (x,y) и т.д.
в точке (x,y) если они существуют, называются частными производными второго порядка в точке (x,y) и т.д.
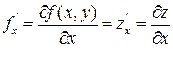
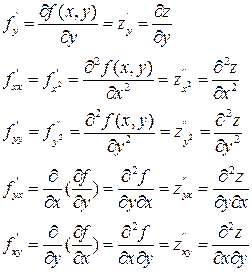
Аналогично определяются частные производные более высокого порядка.
Для функции  , f определена в области E, z=f(x,y) –частные производные третьего порядка определяются формулами:
, f определена в области E, z=f(x,y) –частные производные третьего порядка определяются формулами:
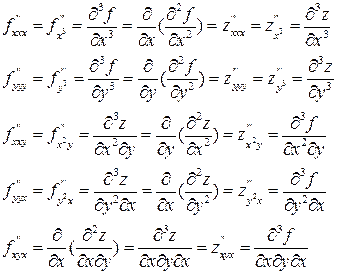
ПРИМЕР.
 .
.
Имеем: 
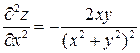 ,
, 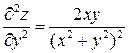 ,
, 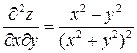 ,
, 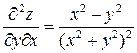 .
.
В этом примере смешанные частные производные равны друг другу. Вообще говоря, значения смешанных производных зависит от порядка, в котором производится последовательные дифференцирования.
Нетрудно заметить, что число частных производных с увеличением порядка возрастает. Однако, некоторые из них при наличии условий совпадают.
Th.1 Пусть  определена вместе со своими частными производными в окрестности
определена вместе со своими частными производными в окрестности  до порядка ”m”.
до порядка ”m”.
Пусть смешанные частные производные m -го порядка непрерывны в точке  .
.
Тогда смешанные частные производные порядка ”m” не зависят от порядка дифференцирования. (Б/Д).
Следует отметить, что это условие достаточное.
Перефразируем Th.1 для случая функции двух переменных.
n=2 m=1:
Пусть 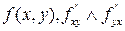 определены в точке
определены в точке 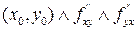 непрерывны в точке
непрерывны в точке  . Тогда, частные производные
. Тогда, частные производные  . (Б/Д).
. (Б/Д).
df.1 Пусть  имеет на G непрерывные частные производные до порядка ”m” включительно. Это обозначаем:
имеет на G непрерывные частные производные до порядка ”m” включительно. Это обозначаем: 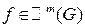 .
.
ПРИМЕР.
 .
.
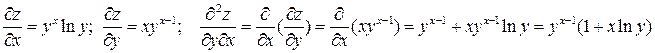

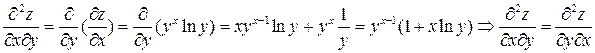 .
.
ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ.
Пусть  и f дифференцируема в окрестности точки
и f дифференцируема в окрестности точки 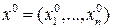 . Рассмотрим дифференциал:
. Рассмотрим дифференциал:
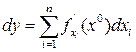 - это дифференциал первого порядка.
- это дифференциал первого порядка.
Вторым дифференциалом функции f в точке  называется дифференциал от первого дифференциала при условиях:
называется дифференциал от первого дифференциала при условиях:
1) дифференциалы независимых переменных  при вычислении вторых дифференциалов остаются постоянными.
при вычислении вторых дифференциалов остаются постоянными.
2) И старые приращения  равны новым приращениям независимых переменных. Обозначение:
равны новым приращениям независимых переменных. Обозначение:
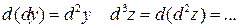
df.2 Дифференциалом порядка “m” функции f в точке 
называется дифференциал от дифференциала порядка “m-1” при тех же предположениях, что и в предыдущем определении.
Th.2 Пусть функция  , тогда
, тогда 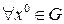 :
:
 (Б/Д).
(Б/Д).
СЛЕДСТВИЕ.
(n=2) Пусть  , тогда
, тогда 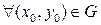 :
:
 , где
, где 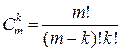
(Б/Д).
В частности если функция  имеет непрерывные частные производные до второго порядка включительно, то, воспользовавшись теоремой о равенстве смешанных производных, получаем:
имеет непрерывные частные производные до второго порядка включительно, то, воспользовавшись теоремой о равенстве смешанных производных, получаем:
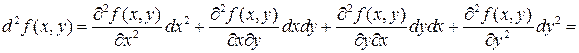
= 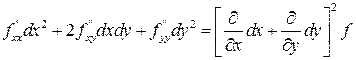 .
.
ЗАМЕЧАНИЕ.
Если ввести формально дифференциальный оператор:
 (1)
(1)
то выражение для дифференциалов можно записать в удобной символической форме:
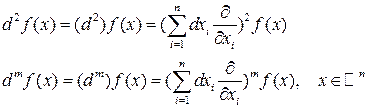
Под произведением дифференциальных операторов понимается их последовательное применение. Например, если 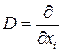 , то
, то

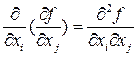 (2)
(2)
 ; При применении дифференциальных операторов вида (1) нужно пользоваться правилом (2). При этом дифференциалы независимых переменных
; При применении дифференциальных операторов вида (1) нужно пользоваться правилом (2). При этом дифференциалы независимых переменных  перемножаются как вещественные числа.
перемножаются как вещественные числа.
ЗАМЕЧАНИЕ.
Для дифференциалов высших порядков инвариантность формы записи не сохраняется.
Th.3 (Формула Тейлора)
Пусть функция 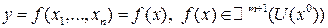
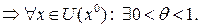 Справедлива формула Тейлора:
Справедлива формула Тейлора:
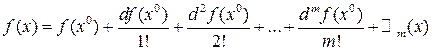
 , где
, где 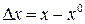 .
.

Следует иметь ввиду 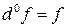 . (Б/Д).
. (Б/Д).
Если n=2 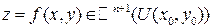 , тогда
, тогда 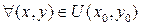 справедлива формула Тейлора:
справедлива формула Тейлора:

+ 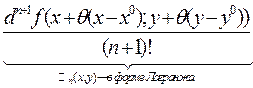 .
.
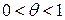 . Если
. Если  - в форме Пеано.
- в форме Пеано.
Следует иметь ввиду: 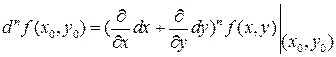 , где
, где
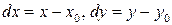 .
.
Date: 2015-09-02; view: 253; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |