
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ознаки збіжності невластивого інтеграла по нескінченному проміжку
Теорема. Якщо на проміжку 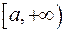 функції
функції  і
і  неперервні і задовольняють нерівність
неперервні і задовольняють нерівність 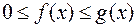 , то
, то
а) якщо збігається інтеграл 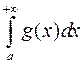 , то збігається і
, то збігається і 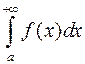 ;
;
б) якщо розбігається інтеграл 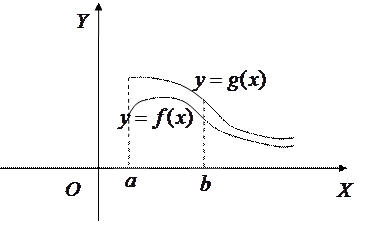
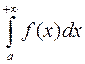 , то розбігається
, то розбігається 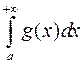 .
.
|
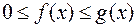 нескінченна фігура, обмежена прямою
нескінченна фігура, обмежена прямою 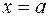 , віссю
, віссю 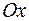 і графіком функції
і графіком функції  , лежить
, лежить
всередині аналогічної фігури, обмеженої згори графіком функції  . Якщо площа більшої фігури є скінченне число (інтеграл
. Якщо площа більшої фігури є скінченне число (інтеграл 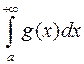 збігається), то і площа меншої фігури є скінчене число (тобто
збігається), то і площа меншої фігури є скінчене число (тобто 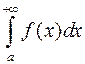 збігається). Якщо ж площа меншої фігури нескінченно велика, то і площа більшої фігури нескінченно велика (інтеграли розбігаються).
збігається). Якщо ж площа меншої фігури нескінченно велика, то і площа більшої фігури нескінченно велика (інтеграли розбігаються).
Приклади. Дослідити на збіжність інтеграли:
а) 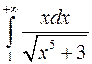 . Оскільки для всіх
. Оскільки для всіх 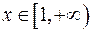 має місце нерівність
має місце нерівність 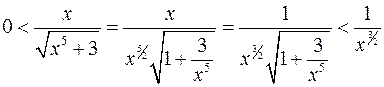 , а
, а 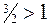 і
і 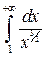 збігається (див. попередній приклад,
збігається (див. попередній приклад, 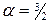 ) то і заданий інтеграл збігається.
) то і заданий інтеграл збігається.
б) 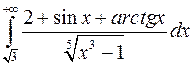 . Цей інтеграл розбігається, тому що для будь-якого
. Цей інтеграл розбігається, тому що для будь-якого 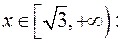
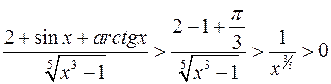 , а інтеграл
, а інтеграл 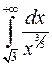 розбігається
розбігається 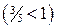 .
.
Теорема (ознака порівняння у граничній формі)
Якщо функції  і
і  неперервні і приймають додатні значення в проміжку
неперервні і приймають додатні значення в проміжку 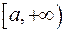 і існує границя
і існує границя  , то інтеграли
, то інтеграли 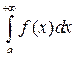 і
і 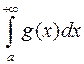 або обидва збігаються, або обидва розбігаються.
або обидва збігаються, або обидва розбігаються.
Ця ознака іноді виявляється зручнішою ніж попередня, бо не вимагає перевірки нерівності 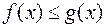 .
.
Приклад. Дослідити на збіжність інтеграл  .
.
Знайдемо границю 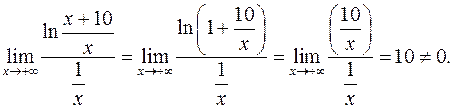
Оскільки 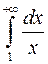 розбігається, то і заданий інтеграл розбігається.
розбігається, то і заданий інтеграл розбігається.
Розглянуті ознаки діють лише при невід’ємних підінтегральних функціях. Якщо ж підінтегральна функція знакозмінна, то в деяких випадках збіжність інтеграла можна встановити за допомогою наступної достатньої ознаки:
Теорема. Якщо збігається інтеграл 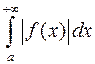 , то збігається і інтеграл
, то збігається і інтеграл 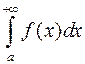 .
.
В цьому разі інтеграл 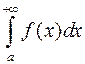 називають абсолютно збіжним.
називають абсолютно збіжним.
Підкреслимо, що дана теорема встановлює достатню, але не необхідну умову збіжності. Тобто для збіжного інтеграла 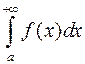 інтеграл
інтеграл 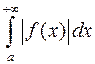 може виявитися розбіжним. В такому разі інтеграл
може виявитися розбіжним. В такому разі інтеграл 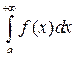 називають умовно (або неабсолютно) збіжним. Отже дана теорема дозволяє виявляти абсолютну збіжність інтеграла від знакозмінної функції, користуючись ознаками збіжності інтегралів від невід’ємних функцій
називають умовно (або неабсолютно) збіжним. Отже дана теорема дозволяє виявляти абсолютну збіжність інтеграла від знакозмінної функції, користуючись ознаками збіжності інтегралів від невід’ємних функцій 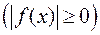 .
.
Приклад. Дослідити на збіжність інтеграл 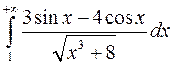 . Тут підінтегральна функція знакозмінна. Оцінимо її абсолютну величину:
. Тут підінтегральна функція знакозмінна. Оцінимо її абсолютну величину: 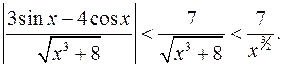 Оскільки інтеграл
Оскільки інтеграл 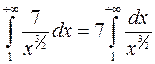 збігається (тому що
збігається (тому що 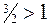 ), то збігається і заданий інтеграл (при чому абсолютно).
), то збігається і заданий інтеграл (при чому абсолютно).
Як уже сказано вище, для знакозмінної підінтегральної функції розглянута ознака виявляє лише абсолютну збіжність інтеграла. Якщо абсолютної збіжності немає, то подальше дослідження інтеграла вимагає застосування більш тонких ознак, які тут не розглядаються.
Date: 2015-09-02; view: 358; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |
