
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основні властивості визначеного інтеграла
1) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю: 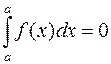 .
.
2) Від переставлення меж інтегрування інтеграл змінює знак на протилежний:  .
.
Властивості 1) і 2) приймаються за означенням. Вони підказані процедурою означення інтеграла і виправдовуються далі способом обчислення інтеграла (формулою Ньютона-Лейбніца).
3) Cталий множник можна винести за знак визначеного інтеграла: 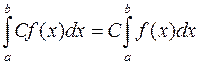
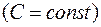 .
.
Справді: 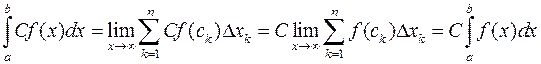 .
.
` 4) Визначений інтеграл від суми інтегровних функцій дорівнює сумі інтегралів від цих функцій: 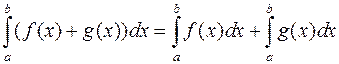 .
.
Для довільного розбиття відрізка
маємо: 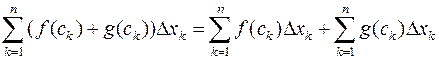 , звідки, переходячи до границі при
, звідки, переходячи до границі при 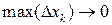 , отримаємо сформульовану властивість. Ця властивість очевидним чином поширюється на випадок будь-якого скінченного числа доданків.
, отримаємо сформульовану властивість. Ця властивість очевидним чином поширюється на випадок будь-якого скінченного числа доданків.
Властивості 3) і 4) складають властивість лінійності визначеного інтеграла.
5) Якщо проміжок інтегрувння розбити на скінченну кількість частинних проміжків, то інтеграл по всьому проміжку дорівнює сумі інтегралів по частинних проміжках (властивість адитивності).
Нехай функція 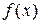 інтегрована на відрізку
інтегрована на відрізку 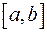 і
і 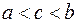 . Покажемо, що
. Покажемо, що 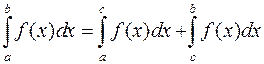 . Оскільки границя інтегральної суми не залежить від способу розбиття відрізка
. Оскільки границя інтегральної суми не залежить від способу розбиття відрізка 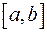 , то розіб’ємо його так, щоб точка
, то розіб’ємо його так, щоб точка 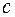 була точкою розбиття, наприклад
була точкою розбиття, наприклад  . Тоди інтегральну суму можна розбити на дві суми:
. Тоди інтегральну суму можна розбити на дві суми:  .
.
Переходячи в цій рівності до границі при 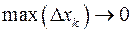 , отримуємо
, отримуємо 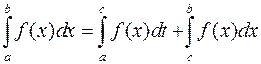 .
.
Результат очевидним чином розповсюджується на випадок, коли проміжок 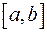 розбивається на будь-яку скінченню кількість частинних проміжків. Зазначимо, що дана властивість стає цілком наочною, якщо розглянути її з точки зору геометричного тлумачення інтеграла.
розбивається на будь-яку скінченню кількість частинних проміжків. Зазначимо, що дана властивість стає цілком наочною, якщо розглянути її з точки зору геометричного тлумачення інтеграла.
6)Нерівність можна почленно інтегрувати: якщо 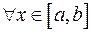 маємо
маємо 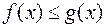 , то
, то 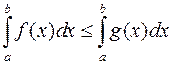
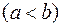 .
.
Побудувавши інтегральні суми для цих інтегралів (при одному й тому ж розбиттю) маємо
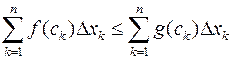 ,
,
бо за умовою 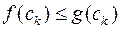 для всіх
для всіх 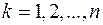 . Переходячи до границі при
. Переходячи до границі при 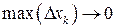 , одержуємо
, одержуємо 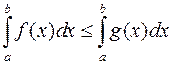 .
.
7) Модуль визначеного інтеграла менший або рівний інтегралові від модуля підінтегральної функції: якщо функція  інтегровна на відрізку
інтегровна на відрізку 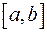 , то
, то 
 .
.
Застосовуючи попередню властивість до нерівності 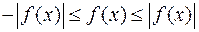 , отримуємо
, отримуємо 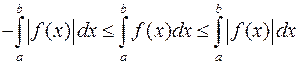 , а це і означає, що
, а це і означає, що  .
.
8) Інтеграл від одиничної функції дорівнює довжині проміжка інтегрування: 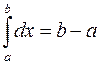 .
.
Справді, відповідна інтегральна сума
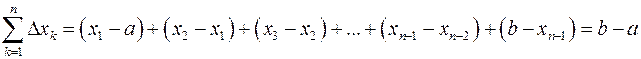
при будь-якому розбитті, отже  .
.
9) Якщо 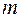 і
і  відповідно найменше і найбільше значення функції
відповідно найменше і найбільше значення функції  на відрізку
на відрізку 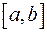
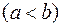 , то
, то

(теорема про оцінку інтеграла).
За умовою 
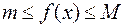 . На підставі властивості 6)
. На підставі властивості 6) 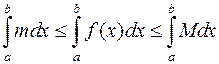 , звідки, застосовуючи властивості 3) і 8)
, звідки, застосовуючи властивості 3) і 8)
отримуємо потрібну нерівність:  .
.
Означення. Поділимо щойно одержану нерівність почленно на 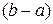 :
:

Число 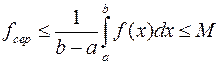 називається середнім значенням функції
називається середнім значенням функції  на відрізку
на відрізку 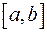 . Оскільки
. Оскільки 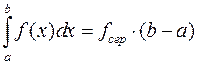 , то
, то 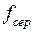 є висота прямокутника, основною якого є відрізок
є висота прямокутника, основною якого є відрізок 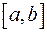 , а площа дорівнює площі криволінійної трапеції, обмеженої прямими
, а площа дорівнює площі криволінійної трапеції, обмеженої прямими 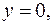
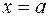 ,
, 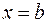 і кривою
і кривою 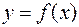 .
.
10) Якщо функція  неперервна на відрізку
неперервна на відрізку 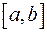 , то існує така точка
, то існує така точка 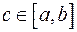 , що
, що 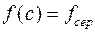 (теорема про середнє значення функції).
(теорема про середнє значення функції).
Справді, функція, неперервна на відрізку, набуває всіх проміжних значень між її найменшим і найбільшим значенням (теорема Коші). Отже існує принаймні одна точка 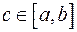 така, що
така, що 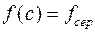 .
.
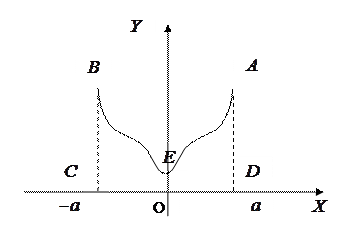
11) Інтеграли від парної і 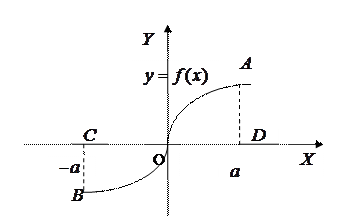 непарної функції в симетричних межах.
непарної функції в симетричних межах.

 а) Якщо
а) Якщо  непарна функція
непарна функція 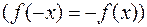 , то
, то 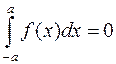 .
.
|
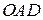 = площі
= площі 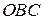 . Але
. Але 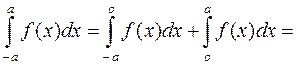
 = -площа
= -площа 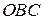 + площа
+ площа 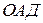
 на підставі властивості 5) і геометричного змісту інтеграла.
на підставі властивості 5) і геометричного змісту інтеграла.
б) Якщо  парна функція
парна функція 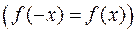 , то
, то 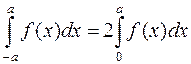 .
. 
|
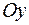 , тому площа
, тому площа 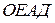 = площі
= площі  (див. рис. 3)
(див. рис. 3)
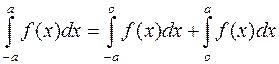 = – площа
= – площа  + площа
+ площа 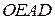 =
=
=2 площі 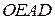 =
= 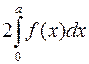 .
.
На завершення переліку основних властивостей інтеграла рекомендуємо читачеві самостійно з’ясувати геометричну інтерпретацію кожної з властивостей.
Date: 2015-09-02; view: 707; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |
