Перегиба

Предположим, что функция f (x) дифференцируема в любой точке интервала (a,b). Тогда в каждой точке имеется касательная к графику, причем она не параллельна оси Оy (ибо ее угловой коэффициент 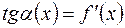конечен).

Определение.

Будем говорить, что график функции y=f (x) имеет на интервале (a,b) выпуклость, направленную вниз (кривая вогнутая), если график в пределах интервала лежит не ниже любой своей касательной.

Если график лежит не выше любой своей касательной, будем говорить, что график имеет выпуклость, направленную вверх (кривая выпуклая).

Примеры.

Вогнутая кривая Выпуклая кривая

(выпуклость направлена вниз) (выпуклость направлена

вверх)

Теорема.

Если функция y=f (x) имеет на интервале (a,b) конечную вторую производную и если эта производная не отрицательна (не положительна) всюду на этом интервале, то график функции y=f (x) имеет на интервале (a,b) выпуклость, направленную вниз (вверх).

Мнемоническое правило.

Если в сосуд набирается вода, то «+», 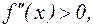выпуклость направлена вниз. Если вода не набирается, 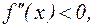то знак «–», выпуклость направлена вверх.

Доказательство.

Для определенности рассмотрим случай, когда всюду на (a,b). Обозначим через c любую точку интервала (a,b) (см. рис.).

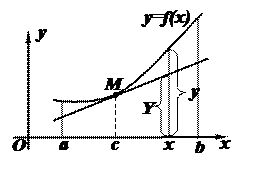Требуется доказать, что график функции f (x) лежит не ниже касательной, проходящей через точку 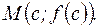Запишем уравнение касательной, проходящей через точку М:

(1)

Разложим f (x) в окрестности точки с по формуле Тейлора, взяв в этой формуле два члена (n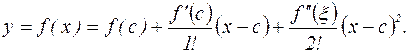=2):

(2)

Здесь учтен остаточный член 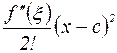в форме Лагранжа; 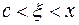. Поскольку по условию 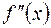существует всюду на (a,b), формула (2) справедлива для любого 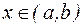. Вычитая из (2) (1), получим:

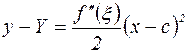
Поскольку 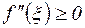всюду на (a,b), то

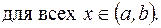
А это и означает, что график функции y=f (x) находится не ниже, чем касательная.

Аналогично доказывается случай, когда .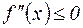

Итак, что же мы получили? Направление выпуклости графика функции полностью характеризуется знаком второй производной этой функции.

Таким образом, первая производная определяет, в каких точках имеется максимум или минимум и на каких интервалах функция возрастает или убывает, а вторая производная определяет те интервалы, на которых функция выпукла вверх или вниз.

Точки перегиба графика функции

Определение.

Точка 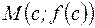графика функции y=f (x) называется точкой перегиба этого графика, если существует такая окрестность точки с, в пределах которой график слева и справа от точки с имеет разные направления выпуклости.

Пример. Рассмотрим график y=sinx.

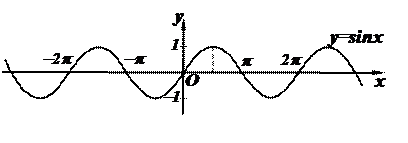На интервале функция y=sinx имеет выпуклость, направленную вниз, на интервале 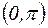выпуклость направлена вверх, точка х=0 – точка перегиба графика.

Оказывается, что для этого графика все точки 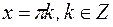– точки перегиба.

Теорема (необходимые условия перегиба) (без доказательства).

Если функция f (x) имеет в точке с вторую производную 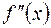и график этой функции имеет перегиб в точке

Пример.

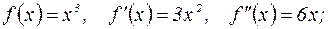если x<0, то , выпуклость графика направлена вверх. Если x>0, то , выпуклость направлена вниз. В точке х=0 имеется перегиб графика, поэтому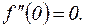

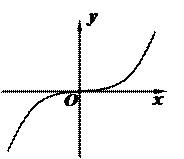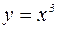
Пример, иллюстрирующий, что условие 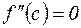не является достаточным условием перегиба: 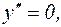но перегиба нет, т.к. 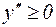при всех х. График имеет вид:

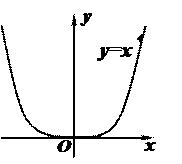
В точке х=0 но

перегиба нет.

Поэтому надо иметь достаточный признак существования перегиба графика.

Теорема (достаточное условие перегиба).

Пусть функция y=f (x) имеет вторую производную в некоторой окрестности точки с и Тогда, если в пределах указанной окрестности вторая производная 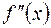имеет разные знаки слева и справа от c, то график этой функции имеет перегиб в точке c.

Теперь все встало на свои места: смена знака первой производной определяет наличие экстремума, а смена знака второй производной определяет наличие перегиба графика.

Date: 2015-09-02; view: 421; Нарушение авторских прав