Функция. Предел функции

1. ОПРЕДЕЛЕНИЕ ФУНКЦИИ

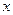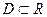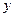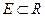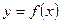О п р е д е л е н и е 1. Если каждому элементу из множества по некоторому правилу соответствует единственный элемент из множества , то говорят, что на множестве задана функция переменной 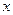. При этом множество называется областью определения функции, а множество 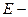областью значений функции.

О п р е д е л е н и е 2. Функция область определения которой симметрична относительно нуля, называется четной, если для всех 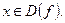График четной функции симметричен относительно оси Оy.

Функция область определения которой симметрична относительно нуля, называется нечетной, если для всех 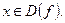График нечетной функции симметричен относительно начала координат.

Функция, не являющаяся ни четной, ни нечетной, называется функцией общего вида.

О п р е д е л е н и е 3. Функция называется

Т– периодической, а число Т называется ее главным периодом, если существует такое наименьшее положительное число Т, что при всех 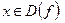выполняется равенство:

.

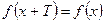О п р е д е л е н и е 4. Графиком функции называется множество точек плоскости Oхy c координатами

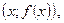где .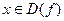

О п р е д е л е н и е 5. Пусть функция 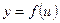определена на множестве 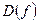, а функция для всех 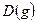, причем 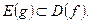Тогда функция 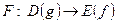, определяемая по правилу

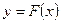, где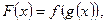

называется сложной функцией (функцией от функции или суперпозицией функци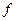й и ).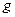

О п р е д е л е н и е 6. Пусть задана функция , отображающая множество 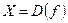на множество 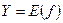взаимно однозначно. Функция называется обратной к функции , если любому 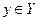поставлено в соответствие то значение 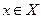, для которого справедливо равенство , то есть

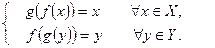
При этом .

З а м е ч а н и е 1. Графики функций и 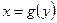представляют одну и ту же кривую. Если же у обратной функции независимую переменную обозначить через 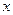, а зависимую - 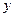, то графики функций и будут симметричны относительно биссектрисы первого и третьего координатных углов.