Количество граней пирамиды равно её количеству вершин

Глава 1. Теоретическое изучение видов сечений и методов их построения в правильной четырехугольной пирамиде

Пирамида (др.-греч. Πυραμίς, род. П. πυραμίδος) — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. Д. Пирамида является частным случаем конуса.

Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Первый, кто установил, чему равен объем пирамиды, был Демокрит, а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.

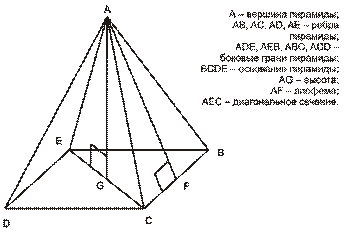
Элементы пирамиды

· апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины;

· боковые грани — треугольники, сходящиеся в вершине пирамиды;

· боковые ребра — общие стороны боковых граней;

· вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;

· высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);

· диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;

· основание — многоугольник, которому не принадлежит вершина пирамиды.

Свойства пирамиды:

Количество граней пирамиды равно её количеству вершин.

Любой многогранник у которого количество граней равно количеству вершин является пирамидой. Общее количество вершин в пирамиде равно n+1, где n – количество вершин в основании.

Если все боковые ребра равны, то:

§ около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;

§ боковые ребра образуют с плоскостью основания равные углы.

§ также верно и обратное, то есть если боковые ребра образуют с плоскостью основания равные углы или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

Если боковые грани наклонены к плоскости основания под одним углом, то:

§ в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;

§ высоты боковых граней равны;

§ площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.

Виды сечений в правильной четырехугольной пирамиде:

· диагональное сечение пирамиды;

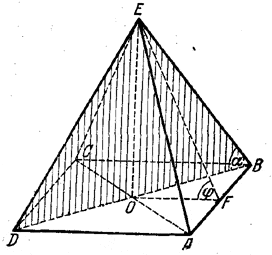
· осевое сечение;

· четырехугольник (трапеция);

· пятиугольник;

· квадрат;

Date: 2015-09-02; view: 5365; Нарушение авторских прав