Символика

Лейбниц одновременно с Ньютоном и независимо от него открыл основные принципы дифференциального и интегрального исчислений. Теория приобрела силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирование - взаимно обратные операции. Об этом свойстве хорошо знал и Ньютон. Но только Лейбниц увидел здесь ту замечательную возможность, которую открывает применение символического метода.

Любой человек, изучив небольшое число правил действия с символами, обозначающими операции дифференцирования и интегрирования, становится обладателем мощного математического метода. В наше время такие символы операций называют операторами. Операторы дифференцирования d() и интегрирования 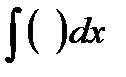действуют на функции, “перерабатывая” их в другие, точно вычисляемые функции. Лейбниц разрабатывает особую алгебру действий с этими операторами. Он доказывает, что обычное число а можно выносить за знак оператора:

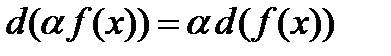
Одинаковые операторы можно выносить за скобку:

или:

Сокращенно все перечисленные свойства можно выразить соотношением:

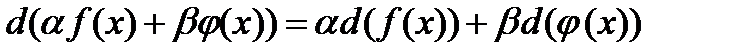
где: a и b - числа.

Операторы. которые обладают таким свойством. называются линейными. Теория линейных операторов, которую с таким успехом начал развивать, Лейбниц,. в современной математике является хорошо разработанной и полезной в приложениях теорией.

Многократное применение операторов можно принимать как степень оператора, например, для d():

То, что основные операторы математического анализа являются взаимно обратными Лейбниц подчёркивал своей символикой, утверждая, что в d(x) и 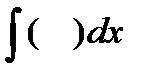также взаимно обратны, как степени и корни в обычном исчислении. Употребляя так же обозначение, аналогичное обозначению a-1 числа, обратного a, причём произведение a×a-1=1. Обозначая операторы 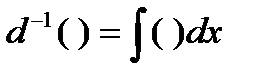или наоборот:

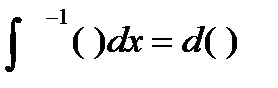
и понимая под их произведением последовательное их применение, имеем:

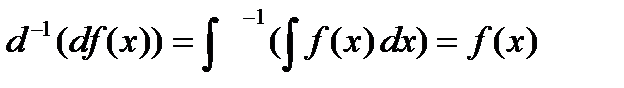
т. е. произведение есть “единица”, не меняющая функцию.

Однако, в подходе Ньютона-Лейбница крылось серьёзное противоречие.

Лейбниц и его последователи - братья Бернулли, Лопиталь и другие - трактовали дифференциалы как бесконечно малые разности обычных конечных величин, как тогда говорили - “реальных” величин “низшей” математики. Поэтому они обращались с теми и другими одинаково и в исчислении применяли к первым те же приемы, которые справедливы при действиях со вторыми. Вместе с тем выяснилось, что таким образом трактуемым бесконечно малым присуще свойство, противоречащее одному основному свойству основных конечных величин: если А — конечная величина, а a — бесконечно малая, то, чтобы результат исчисления получался совершенно точным, оказалось необходимым проводить вычисления в предположении, что А+a=А.

Дифференциальное исчисление, значение которого для развития науки и техники было вне сомнений, оказалось в парадоксальном положении: чтобы его методами получить точный результат, надо было исходить из ошибочного утверждения.

Ньютон пытался обосновать дифференциальное исчисление на законах механики и понятии предела. Но ему не удалось освободить свое исчисление флюксий от недостатков, присущих дифференциальному исчислению Лейбница. В практике вычисления Ньютон, как и Лейбниц, применял принцип отбрасывания бесконечно малых.

Такая непоследовательность позволила назвать дифференциальное исчисление Лейбница–Ньютона мистическим. Этим в первую очередь подчеркивалось, что Лейбниц и Ньютон вводили в дифференциальное исчисление бесконечно малые величины метафизически, сразу полагая их существующими, без выяснения их возникновения и развития и без анализа природы их специфических свойств.

Попытки построить анализ бесконечно малых и теорию рядов в полном соответствии с основными понятиями и истинами “низшей” математики с самого начала к успешным результатам не привели. Поэтому Лейбниц и его последователи пытались оправдать принципы анализа бесконечно малых путем сравнения бесконечно малой с песчинкой, которой можно пренебречь при вычислении высоты горы, посредством ссылок на вероятность и т. п.

Задачи:

Если в истории математики на одной высоте по своему значению стоят годы — 1в65 («чумный» отпуск Ньютона) и 1675 (изобретение дифференциального исчисления Лейбница), то и 1684-й год не уступает им в славе. В этом году в «Acta eruditorum» появилась первая статья Лейбница с изложением основ нового исчисления. Полное название статьи: «Новый метод максимумов и минимумов,а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления». Лейбниц счел необходимым вынести в заголовок статьи то свойство нового исчисления, что дробные и иррациональные величины не служат для него препятствием. В этом свойстве действительно ценное преимущество способа, предлагаемого Лейбницем. Отыскание экстремумов уже было давно и подробно изученной задачей в предыстории дифференциального исчисления. Методы отыскания дали Декарт и Ферма, К сожалению, эти•методы требовали, чтобы иррациональные и дробные выражения были устранены или, иначе, непосредственно могли применяться лишь к алгебраическим кривым. Лейбниц, конечно, отчетливо сознавал преимущество своего исчисления. Изложив основы дифференциального исчисления, он говорит: «... можно будет находить максимумы и минимумы, а также касательные, не испытывая притом необходимости в устранении дробей или иррациональностей или других сложных выражений, как это приходится, однако, делать, если пользоваться доныне опубликованными методами». Немного дальше он снова возвращается к этому же: «Во всех таких и много более сложных случаях наш метод обладает одной и той же поразительной и прямо беспримерной легкостью». Статья, о которой идет речь, отличается крайне сжатым изложением. На каких-нибудь шести страницах изложены основные понятия, правила дифференцирования, отыскание экстремумов, точек перегиба и т. д. Можно вполне согласиться с Иоганном Бернулли, который назвал эту статью «скорее загадкой, чем разъяснением».

Лейбниц предлагает чертеж, часть которого приводится на рис. Ось абсцисс X направлена вертикально, функция изображается кривой v. Дифференциал независимого переменного представлен отрезком произвольной длины dx. Из чертежа непосредственно получается пропорция (не забыть, что dx есть приращение ординаты касательной, а не кривой)

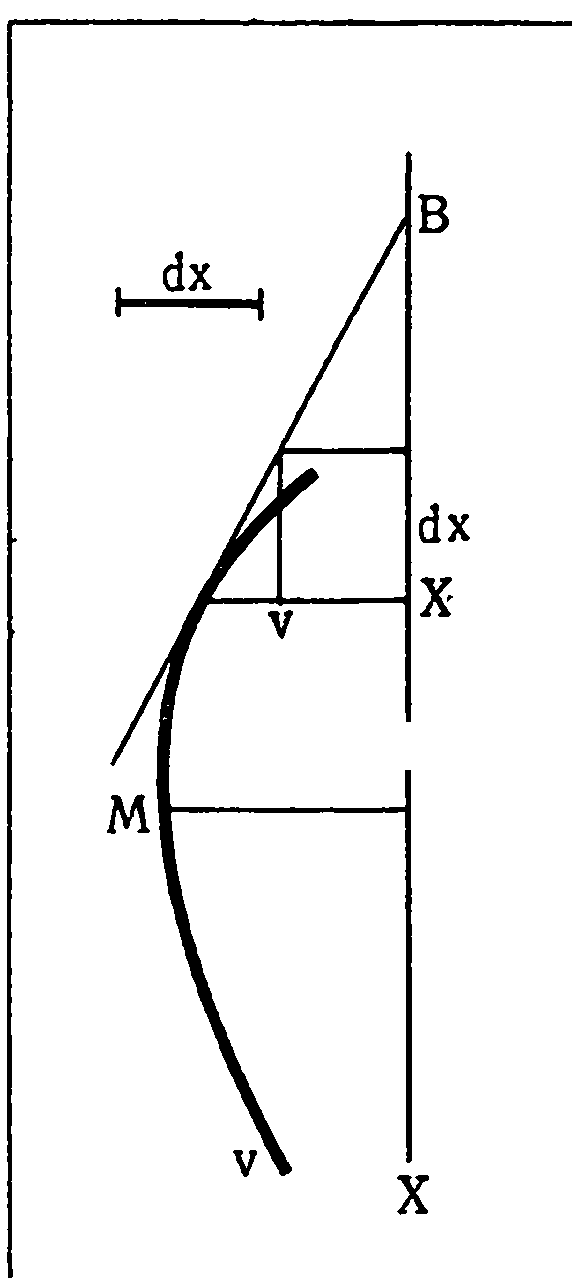
Далее Лейбниц пожелал показать силу своего нового исчисления. Для этой цели он взял ныне очень известную задачу Дебона.

В общем виде задача Дебона ставится в следующей форме: найти кривую, подкасательная которой есть заданная функция. На современном языке эта задача означает не что иное, как необходимость проинтегрировать дифференциальное уравнение первого порядка: f(x, у, у') = 0. Задача: «Требуется найти линию ww, обладающую такой природой, что если wc есть проведенная к оси касательная, то Хс всегда равно постоянному отрезку а».

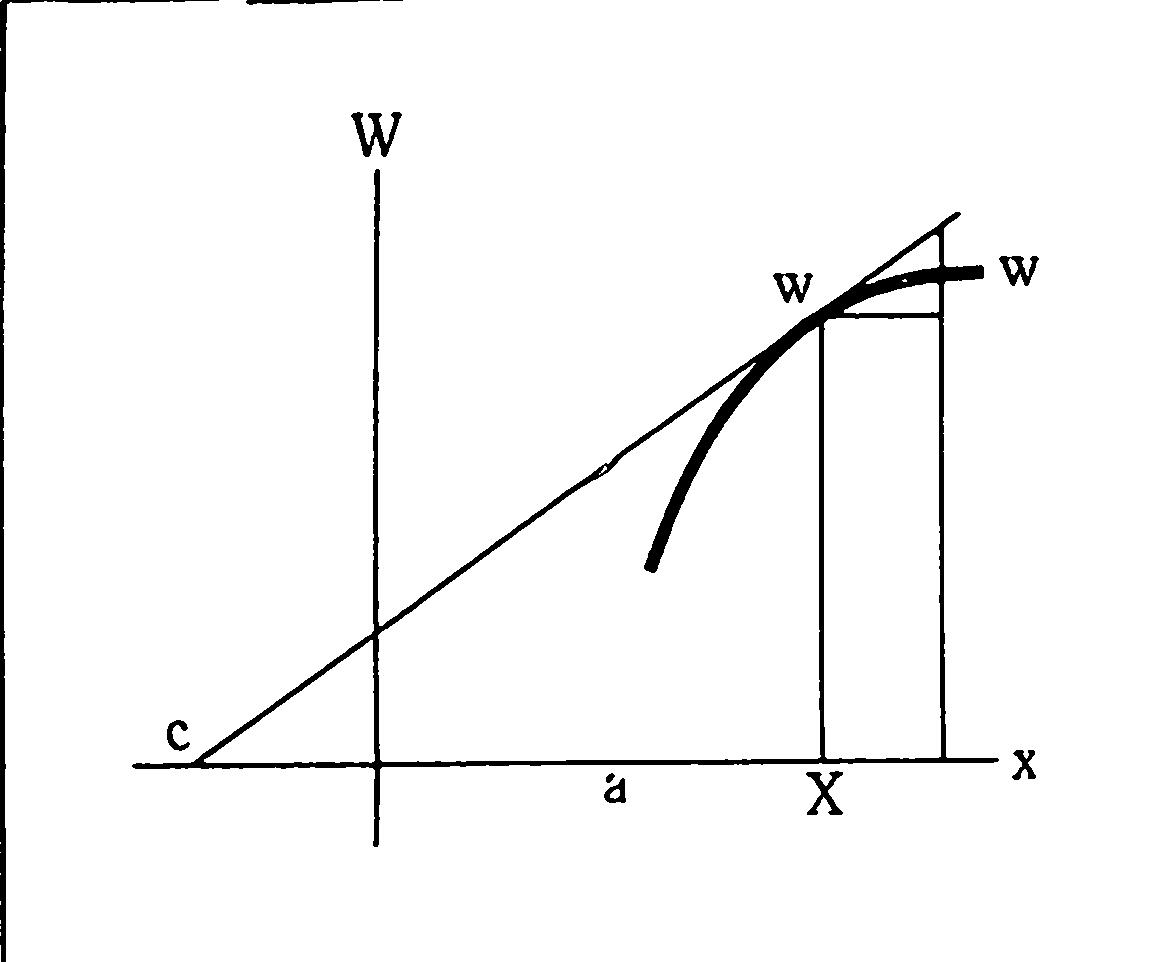
Решение Лейбница: из чертежа видно, что w/a — dw/dx полагая dx= b = const (дифференциал независимого переменного Лейбниц и его ученики считали постоянной величиной), имеем w= dw; в настоящее время уравнение Лейбница привели бы к виду 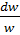= Cdx, откуда мгновенно следует w = D 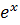, но Лейбниц не имел возможности так рассуждать, поэтому он говорит следующее: если w пропорционально dw, то w образует геометрическую прогрессию, когда х — арифметическую, а в таком случае х есть логарифм w. Следовательно, ww есть логарифмическая кривая. Задача решена.

Разработка «суммирующего» или «сумматорного» исчисления шла одновременно с продвижением в области дифференциального исчисления и его приложений.

Уже в 1686 г. Лейбниц публикует в «Acta eruditorum» статью об этом исчислении.

Задача, которую он решает в этой работе, очень проста, но тем не менее для старых методов или, как их называл Лейбниц, для доныне опубликованных методов, была непосильной. Можно ее сформулировать так: дана поднормаль кривой как заданная функция независимого переменного, найти эту кривую.

Лейбниц решает задачу следующим образом. Он рассматривает два треугольника: один — составленный из поднормали р, ординаты у и нормали, второй — составленный из дифференциалов dy, dx и ds. Из подобия треугольников получает равенство pdx = ydy. Далее он говорит: «...и если обратить дифференциальное уравнение в суммирующее, то будет ».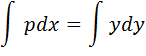

Способ, используемый Лейбницем для получения окончательного результата, заслуживает не меньшего внимания. О выражении 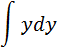автор говорит: так как 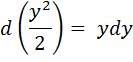, то 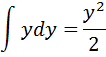, потому что «у нас суммы и разности или 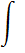и так же взаимно обратны, как степени и корни в обыкновенном исчислении».

Таким образом устанавливается взаимная обратность обоих исчислений.

Здесь впервые в ясной форме и вполне определенно устанавливается связь между дифференциальным и суммирующим исчислениями Лейбница. То, что выглядит совершенно естественным и как бы само собой разумеющимся для нашего современника, в действительности требовало громадного изобретательского таланта