
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Перевод чисел из одной системы счисления в другую
Правило перевода целых чисел из десятичной системы счисления в систему с основанием q:
1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.
2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).
Оборудование: дидактические материалы по теме «Двоичное кодирование информации».
Последовательность выполнения:
1. Разберите решение примеров и запишите примеры перевода чисел в тетрадь.
Пример 1. Перевести 2610 в двоичную систему счисления.
Решение:

Ответ: 2610=110102
Пример 2. Перевести 1910 в троичную систему счисления.
Решение:

Ответ: 1910=2013.
Пример 3. Перевести 24110 в восьмеричную систему счисления.
Решение:
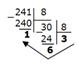
Ответ: 24110=3618.
Пример 4. Перевести 362710 в шестнадцатеричную систему счисления. Решение:

Т.к. в шестнадцатеричной системе счисления 14 – Е, а 11 – В, то получаем ответ Е2В16.
Ответ: 362710=E2B16.
2. Решите следующие задания. Результат оформите в тетради.
Задание 1. Переведите десятичные числа в заданные системы счисления.
| № варианта | в двоичную | в восьмеричную | в шестнадцатеричную |
Задание 2. Преобразуйте десятичные числа в двоичные и восьмеричные.
| № варианта | число | № варианта | число |
Задание 3. Переведите в двоичную систему десятичные числа.
| № варианта | число | № варианта | число |
| 0,625 | 0,75 | ||
| 0,28125 | 7/16 | ||
| 0,078125 | 3/8 | ||
| 0,34375 | 1/4 | ||
| 0,25 | 0,515625 |
Контрольные вопросы:
1. Что такое система счисления?
2. Что такое основание системы счисления?
3. Что такое непозиционная система счисления?
4. Что такое позиционная система счисления?
5. Из каких знаков состоит алфавит десятичной и двоичной систем?
Практическая работа 9. Перевод целых чисел в десятичную систему счисления
Цель работы: приобретение навыка перевода целых чисел в десятичную СС
Краткое теоретическое обоснование:
Правило: Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления.
Для любой позиционной системы счисления справедливо следующее правило формирования числа на основании входящих в эту систему цифр:
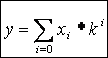 , (1)
, (1)
или, если расписать сумму в этом выражении,
 , где
, где
y – число;
k – основание системы счисления;
xi – цифры числа;
i – номер позиции (разряда) числа, начиная с 0.
Так, на основании формулы (1) десятичное число 63810 представляется следующим образом:
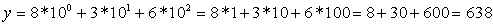
Оборудование: дидактические материалы по теме «Двоичное кодирование информации».
Последовательность выполнения:
1. Разберите решение примеров и запишите примеры перевода чисел в тетрадь.
Пример 1. Перевести число 1101102 из двоичной системы счисления в десятичную.
Решение: 1101102 = 1*25 + 1*24 + 0*23+1*22+1*21+0*20=32+16+4+2=5410.
Ответ: 1101102 = 5410.
Пример 2. Перевести число 101,012 из двоичной системы счисления в десятичную.
Решение:101,012 = 1*22 + 0*21 + 1*20+0*2-1+1*2-2 =4+0+1+0+0,25=5,2510.
Ответ: 101,012 = 5,2510.
Пример 3. Перевести число 1221003 из троичной системы счисления в десятичную.
Решение: 122013=1*34 + 2*33 + 2*32 + 0*31 + 1*30 = 81+54+18+1 = 15410.
Ответ: 122013 = 15410.
Пример 4. Перевести число 1637 из семеричной системы счисления в десятичную.
Решение: 1637 = 1*72 + 6*71 + 3*70 = 49+42+3= 9410.
Ответ: 1637 = 9410.
Пример5. Перевести число 2Е16 в десятичную систему счисления.
Решение: 2Е16 = 2*161 +14*160 = 32 +14 = 4610.
Ответ: 2Е16 = 4610.
2. Решите следующие задания. Результат оформите в тетради.
Задание 1. Переведите в десятичную систему счисления следующие числа
| № варианта | |||
| 220,7 | А9Е,1 | ||
| 11011,01 | 35,6 | 15А | |
| 40,5 | 2FA | ||
| 111011.101 | 13,7 | 3C,1 | |
| 27,31 | 2FВ | ||
| 101001,11 | 37,4 | 19,А | |
| 100100,1 | 65,3 | 2F,А | |
| 43,5 | 1С,4 | ||
| 101011,01 | 72,2 | АD,3 | |
| 101101,110 | 30,1 | 38,В |
Задание 2. Преобразуйте двоичные числа в восьмеричные и десятичные.
| № варианта | число | № варианта | число |
Задание 3. Выполните Практикум 13. из учебника И.К. Сафронов «Задачник-практикум по информатике» на стр. 35. Номер варианта определяется по номеру рабочего места. Решение представить в развернутом виде в тетради.
Контрольные вопросы:
1. Почему в вычислительной технике взята за основу двоичная система счисления?
2. Опишите порядок действий при переводе целых чисел из двоичной СС в десятичную СС.
3. Опишите порядок действий при переводе целых чисел из восьмеричной СС в десятичную СС.
4. Опишите порядок действий при переводе целых чисел из шестнадцатеричной СС в десятичную СС.
Практическая работа 10. Перевод целых чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную
Цель работы: приобретение навыка перевода целых чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную СС
Краткое теоретическое обоснование:
Правило перевода целых чисел: Чтобы перевести целое двоичное число в восьмеричную (8=23) систему счисления необходимо:
1. разбить данное число справа налево на группы по 3 цифры в каждой;
2. рассмотреть каждую группу и записать ее соответствующей цифрой восьмеричной системы счисления.
Правило: Чтобы перевести целое двоичное число в шестнадцатеричную (16=24) систему счисления необходимо:
1. разбить данное число справа налево на группы по 4 цифры в каждой;
2. рассмотреть каждую группу и записать ее соответствующей цифрой шестнадцатеричной системы счисления.
Оборудование: дидактические материалы по теме «Двоичное кодирование информации».
Последовательность выполнения:
1. Разберите решение примеров и запишите примеры перевода чисел в тетрадь.
Пример 1. Перевести число 111100000101102 в восьмеричную систему счисления.
Решение:
111 110 000 010 110
7 6 0 2 6
Ответ: 111100000101102= 760268.
Пример 2. Перевести число 111000102 в шестнадцатеричную систему счисления.
Решение:
1110 0010
Е 2
Ответ: 111000102 = Е216.
2. Выполните из учебника И.К. Сафронов «Задачник-практикум по информатике». Практикум 11 на стр. 33. Номер варианта определяется по номеру рабочего места. Решение по переводу чисел представить в тетради.
Контрольные вопросы:
1. Какое наибольшее десятичное число можно записать тремя цифрами:
· в двоичной системе;
· в восьмеричной системе;
· в шестнадцатеричной системе?
2. Как осуществляется сложение и умножение двоичных чисел?
Лабораторная работа 1. Системы счисления: перевод чисел
Цель работы: организация средствами Excel автоматического выполнения операций над представлениями чисел в позиционных системах счисления.
Краткое теоретическое обоснование: Лабораторная работа выполняется три учебных занятия.
Содержание работы на занятии:
1. Реализация перевода чисел в десятичную систему счисления.
2. Реализация перевода чисел из десятичной системы счисления.
3. Сложение чисел в позиционных системах счисления. Проведение экспериментов и решение задач.
Оборудование: Персональные компьютеры. Программа Excel.
Последовательность выполнения:
· Для выполнения этой работы создайте в вашей папке файл – приложение Excel – с именем «Системы счисления» и откройте его. Дайте трем листам имена: «В десятичную» «Из десятичной» и «Сложение».
· Все три листа нужно сделать «в клеточку», т. е. задать ширину их столбцов примерно равной ширине строк до 2.00. Результат – все столбцы сделались одной ширины, и ячейки приобрели форму квадратных клеточек.
· Перейдем к листу «В десятичную».
На листе создадим «машину» для перевода в десятичную систему чисел, записываемых в системах счисления с любым основанием B >1.С этой целью разметим предварительно лист так, как показано на рис. 1.
В верхней части листа наберите текст - заголовок листа: «Перевод чисел из системы счисления с основанием B в десятичную систему счисления». Растяните в ширину столбец В, в котором будем записывать основание системы счисления (в ячейку В8) и получать десятичное число – результат перевода (ячейка В15). С помощью команды-кнопки меню Внешние границы разметьте диапазон для записи цифр целой части числа (D8:W8) и дробной части числа (Y8:AR8). Сделайте необходимые текстовые надписи – пояснения к этим размеченным диапазонам ячеек. Соседние с размеченными диапазонами ячейки можно залить серым цветом для улучшения дизайна нашей «машины» (рис. 1).
Если вся «машина» не помещается на экране, то можно слегка уменьшить масштаб листа.
Рис. 1. Примерный вид экрана с листом «В десятичную»
Строка 8 листа готова для записи в ячейку В8 основания системы счисления и для записи в ячейки D8:AR8 цифр числа, представленного в этой системе счисления. При этом как целая, так и дробная части числа могут содержать до 20 цифр. Остается сделать так, чтобы в ячейке В15 появлялось десятичное число, записанное в строке 8 в системе счисления с основанием В. Для этого нужно правильно ввести в ячейки несколько простых формул.
Во всех этих формулах нужно будет ссылаться на одну и ту же ячейку В8. И, чтобы при копировании формул ссылка на эту ячейку не изменялась, эту ссылку нужно писать как абсолютную, т. е. в виде $В$8. Однако наличие ссылок такого вида в формулах делает их не очень удобными для чтения. Поэтому воспользуемся другим механизмом присвоения абсолютного имени ячейкам и диапазонам. Чтобы присвоить ячейке В8 имя, например а, выделим ее левой кнопкой мыши. Взгляните на поле имени – оно расположено на верхней панели инструментов, слева от строки формул. Введите в поле имени букву а и нажмите Enter. Имя, присвоенное сейчас выделенной ячейке, является ее абсолютным адресом, уникальным в пределах всей книги. Если, например, сейчас вы перейдете на другой лист и в поле имени выберете из списка имя а, то тут же окажетесь вновь на листе «В десятичную», где будет выделена ячейка В8. Итак, основание системы счисления будет именоваться на листе как а, и в формулах вместо $В$8 мы будем писать просто букву а.
Введите в ячейку В8 в качестве основания системы счисления число 3. Для перевода чисел в десятичную систему зададим веса разрядов. В ячейку W10 (т. е. под младшим разрядом целой части) введите 1 – это вес младшего разряда.
В соседнюю слева ячейку введите формулу =W10* а. В ней появится число 3. Скопируйте эту ячейку с формулой ее «растягиванием» за маркер заполнения влево, до старшего разряда. Теперь мы имеем все веса целой части числа. Многие их значения не входят в клеточки и выводятся как символ решетки. Но нам и не нужно их видеть. Скоро мы скроем всю эту строку.
Аналогично задайте веса для дробной части числа: в клетку Y10 введите формулу =1/ а. Результат из-за его округления до одной цифры будет выглядеть как 0. В соседнюю справа ячейку введите формулу =Y10/ а. Затем «растяните» – скопируйте ее до младшего разряда дробной части. Теперь в ячейку В15 введите формулу:
=СУММПРОИЗВ(D8:W8;D10:W10)+СУММПРОИЗВ(Y8:AR8;Y10:AR10)
Программа для перевода чисел в десятичную систему счисления готова.
Формулу для вычисления суммы произведений цифр разрядов на их веса пришлось разбить на две части, т. к., из-за дизайнерских соображений в колонке X между двумя диапазонами разрядов поместили запятую.
Если запятую оттуда удалить, то формулу в ячейке В15 можно записать сразу для двух сплошных диапазонов в виде СУММПРОИЗ(D8:AR8;D10:AR10). Запишите в ячейки W8 и Y8 цифры 1 и 1. Остальные разряды троичного числа пусть будут нули (или пустые ячейки – это то же самое). Таким образом, мы ввели троичное число 1,13. В ячейке В15 появится десятичное изображение 1,3333… этого троичного числа. Увеличьте ширину столбца B, как на рис. 1 или еще больше.
Выделите все ячейки с входными данными: для этого щелкните ячейку B8 и при нажатой клавише Ctrl выделите мышкой диапазон D8:AR8. После выделения войдите в меню Формат/Ячейки..., в открывшемся окне на вкладке Защита снимите флажок Защищаемая ячейка и подтвердите это действие клавишей ОК. Теперь выделенные нами ячейки останутся доступными для ввода данных после защиты листа. Затем выделите строки 10 и 11, щелкните по ним правой клавишей мыши и выберите из контекстного меню Скрыть. Чтобы защитить лист, войдите в меню Сервис/Защита/Защитить лист и нажмите ОК, не задавая пароль. Снимать защиту листа можно будет без пароля, через те же пункты меню Сервис/Защита.
Так мы застраховались от случайного изменения всех ячеек, кроме тех, где нужно будет вводить данные при решении задач. Попробуйте выполнить какие-нибудь непредусмотренные изменения, например, отобразить скрытые строки или изменить формулы. Необходимые для этого действия окажутся недоступны.
Можно приступать к экспериментам. Сохраните файл, но не закрывайте его. Первый проверочный опыт можно провести сейчас. Запишите в строке 8 в качестве основания исходной системы счисления число 10. Запишите в этой же строке цифры целой и дробной части числа 1234,5. Эта запись автоматически преобразуется и отобразится в ячейке В15 в виде десятичного числа 1234,5. Теперь в ячейке В8 запишите 8. При таком основании исходной системы счисления число, записанное в строке 8, отобразится в виде десятичного числа 668,625.
· Перейдите на лист «Из десятичной».
Чтобы построить «машину» для перевода десятичных чисел в системы счисления с любыми основаниями, разметьте ячейки: ячейку K7 – для ввода основания системы счисления B, ячейку B10 – для ввода целой части N исходного десятичного числа, и ячейку B18 – для ввода его дробной части Z (см. рис. 2). Присвойте выбранным ячейкам имена b, N и Z, используя окно имен.
Рисунок 2 – Примерная организация листа «Из десятичной»
Обратите внимание: на рис. 2 выделена ячейка K7 с записанным в ней числом 2, а в окне имен (вверху слева) высвечено имя b этой ячейки. Кроме того, строки 11, 12 и 19, 20 (с промежуточными результатами) на листе уже скрыты, нам же эти строки пока еще нужны для работы. Ширину столбца B увеличьте. Сделайте с помощью форматирования границ разметку диапазонов D10:W10 и D18:W18 для отображения цифр переведенного числа. Позднее можно будет поработать и над дизайном листа в целом. В ячейки для записи чисел B, N и Z запишите 2, 1190 и 0,625 соответственно; сейчас мы начнем перевод в двоичную систему счисления десятичного числа 1190,625.
В строках 11 и 12 разместим формулы для пересчета целой части N десятичного числа в заданную систему счисления с любым основанием B, реализуя правило последовательного деления N на B и вычисления остатков [1]. Формулы для определения частных от деления разместим в диапазоне ячеек D11:W11, под разрядами B -ичного числа. Строкой ниже введем формулы для вычисления последовательных остатков от деления N на B. Эти остатки и будут цифрами B -ичного числа.
Итак, введем в ячейку W11, под младшим разрядом, формулу =ЦЕЛОЕ(N/b).
Поскольку результат деления – частное – не помещается в ячейку, то в ней выводится символ «решетка». В соседнюю слева ячейку V11 введем формулу = ЦЕЛОЕ(W11/b). Скопируем эту ячейку влево до старшего разряда, т. е. на весь диапазон D11:V11.
В ячейку W12 запишем формулу =ОСТАТ(N;b), по которой определяется младшая цифра числа. В соседнюю слева ячейку V12 запишем =ОСТАТ(W11;b), т. к. далее мы должны получать остатки от деления каждого предыдущего частного на b. Скопируем эту формулу влево, до старшего разряда, т. е. в диапазон D12:V12.
Мы видим в строке 12 все цифры B -ичного (в данном случае – двоичного) числа, и на этом можно было бы остановиться. Однако потребуем еще, чтобы незначащие нули в старших разрядах не выводились. Тогда переносить полученные цифры в приготовленную для них «разрядную сетку» D10:W10 нужно с помощью условной функции «ЕСЛИ». Сделаем это так.
В клетку W10 введем формулу =W12. Младший разряд переносится в отображаемые цифры безусловно. Левее, в клетку V10, вводим формулу
=ЕСЛИ(СУММ($D$12:V12)=0;””;V12). Смысл этой формулы таков: если слева от разряда V12 (включая и сам этот разряд) все нули, то в ячейку записывается результат «пусто» (пустой текст между апострофами), иначе пишется цифра из ячейки V12. Ячейку V10 с введенной формулой копируем влево до конца разрядной сетки. Если все сделано правильно, то результат перевода соответствует рис. 2.
Дробная часть Z десятичного числа переводится аналогично, только при этом применяется не деление, а умножение Z на основание системы счисления. После каждого умножения целая часть результата забирается (вычитается) из него и переносится в качестве очередной цифры в состав дробной части перевода числа [1]. При этом цифры дробной части появляются в порядке слева направо.
В строках 19 и 20 для такого перевода выполните следующие действия:
– в ячейку D19 введите =b*Z,
– в ячейку D18 введите =ЦЕЛОЕ(D19) – это первая цифра дробной части, – в D20 вводите формулу =D19–D18 – вычитаем целую часть из результата, – в E19 – формулу =b*D20, и скопируйте эту ячейку вправо до W19, – скопируйте ячейку D18 вправо вплоть до W18, – скопируйте ячейку D20 вправо вплоть до W20.
Если все сделано правильно, то цифры дробной части будут как на рис. 2. Теперь скройте строки 11, 12 и 19, 20. Выделите ячейки с исходными данными (K7, B10, B18), через меню формата ячеек снимите с них флажок «защищаемая ячейка» и защитите лист, не задавая пароля. Лист готов к экспериментам и к решению задач. Сохраните файл.
· Работа с листом «Сложение»
Перейдите на этот лист. Разметив ячейки и диапазоны для ввода основания системы счисления, для ввода цифр слагаемых и отображения суммы слагаемых (как на рис. 3), введите в диапазон ячеек D12:AC12 формулы для вычисления переносов. Для этого введите в ячейку B8 число 8, а в ячейку AC12 – формулу =ЦЕЛОЕ((AC9+AC8+AD12)/$B$8). Смысл формулы в том, что когда сумма двух разрядов и переноса из предыдущего разряда будет больше основания системы счисления, то сформируется перенос в следующий разряд. Скопируйте ячейку AC12 с формулой влево до ячейки D12. Аналогично можно задать формулы для вычисления разрядов суммы. В ячейку AC10 занесите формулу =ОСТАТ(AD12+AC8+AC9;$B$8) – это часть той же суммы, остающаяся в данном разряде. Скопируйте эту ячейку влево до конца разрядной сетки.
Рис. 3. Примерный вид листа «Сложение»
Скройте строку 12. Введите цифры семеричных слагаемых как на рис. 3. Если вы не ошибались, то получится и соответствующая этому рисунку сумма. На рис. 3 видно, что группа разрядов чисел «разделена» на листе на две части стрелками. Так можно условно отмечать положение разделительной запятой, когда нужно интерпретировать суммирование как операцию над дробными числами. Здесь, на рис. 3, сложены дробные числа из последнего варианта заданий к данной лабораторной работе (табл. 1). Выделите ячейку B8 и, прижимая клавишу Ctrl, выделите одновременно с ячейкой диапазон D8:AC9. Снимите через меню формата флажок защиты выделенных ячеек, т. к. эти ячейки нужно оставить доступными для ввода данных после защиты всего листа. Защитите лист и сохраните файл.
· Перед тем как выполнять индивидуальные варианты заданий, проведите предлагаемые ниже эксперименты и ответьте на поставленные вопросы.
Эксперимент 1. Случай B >10. На листе «Из десятичной» введите для перевода число
1190,625 (т. е. N = 1190, Z = 0,625) и задайте основание системы счисления 16. Полученное в результате автоматического перевода шестнадцатеричное число изображается так:
Цифры этого числа записаны в виде их десятичных значений. В стандартах информатики данное шестнадцатеричное число записывается в виде 4A6,A. Но, поскольку в выполняемой работе основание B >10 может отличаться от 16 (оно может быть любым), то принятая нами запись цифр числа в виде их десятичных значений представляется достаточно удобной и универсальной.
Ответьте на вопросы.
1) Как представляется число 1190,62510 в двадцатеричной системе счисления?
2) Сколько значащих двадцатеричных цифр оно содержит?
Эксперимент 2. Задайте N = 0 и Z = 0,1. Переведите указанное так десятичное число 0,110 в двоичную систему счисления (т. е. задайте B = 2). В двоичной записи получилась периодическая дробь (0,0001100110011...)2. Переведите десятичную дробь 0,110 в системы счисления с основаниями 2,...,9. Ответьте на следующие вопросы.
1) Почему дробь получается периодической?
2) В каких случаях дробь с конечным числом цифр точно переводится в дробь с конечным числом цифр?
Эксперимент 3. В предыдущем эксперименте, когда вы испытывали вариант B = 8, период дроби представлял собой последовательность цифр 6314, однако в последних двух разрядах результата этот период сбился. Причина сбивки заключается в том, что компьютер использует двоичное внутреннее представление чисел и имеет ограниченную длину разрядной сетки; поэтому построенная нами «машина» для перевода чисел неизбежно округляет дроби во многих промежуточных операциях с ними. При точном переводе периодичность полученной дроби нигде не нарушалась бы.
Ответьте на следующие вопрос: сколько неточных последних разрядов содержат результаты выполняемого «машиной» перевода десятичной дроби 0,110 в системы счисления с основаниями 1) B = 9; 2) B = 11; 3) B = 12?
Эксперимент 4. Переведите в систему счисления с основанием 9 целое число 999999999 (задавая Z =0). В результате получится девятеричное число 2520607100, заканчивающееся двумя нулями.
Ответьте на следующие вопросы:
1) Можно ли было без осуществления перевода предсказать появление в конце числа двух нулей?
2) Сколько нулей будет в конце его троичной записи?
Эксперимент5. Проведите эксперимент, на основе которого выполняются индивидуальные задания к данной лабораторной работе. Суть эксперимента состоит в том, что две заданных величины представляются и складываются сначала в одной (исходной) системе счисления, потом в другой, и результаты сравниваются. Теоретически они, разумеется, должны совпадать точно.
Переведите заданное целое число X 7 = 24607 в десятичную систему счисления, затем из десятичной – в пятеричную. В результате получается преобразование 24607 ® 121445.
Переведите таким же способом число Y 7 = 1337 в пятеричную систему. В результате получится преобразование 1337 ® 2435.
На листе «Сложение» найдите сумму Z сначала семеричных представлений
величин X и Y, а затем – их пятеричных представлений. Получается Z 7 = X 7+ Y 7 = 26237, Z 5 = X 5+ Y 5 = 124425. Переведите эти два разных представления суммы Z в десятичное число с помощью листа «В десятичную». Итог: выполнение операции сложения в обеих системах счисления дает один и тот же результат 99710.
Все выполненные действия описываются такой «программой»:
X B ® X C; Y B ® Y C; X B + Y B = Z B ® Z 10; X C + Y C = Z C ® Z' 10; (1)
при этом в выполненном примере было задано основание исходной системы
счисления B = 7 и основание дублирующей системы C = 5.
Ниже, в индивидуальных вариантах заданий, слагаемые не являются целыми числами. Поскольку при этом перевод и сложение чисел при выполнении «программы» (1) осуществляются с ограниченным числом разрядов, то числа Z 10 и Z' 10 могут точно и не совпасть. Разделительные стрелки на листе «Сложение» расположите приблизительно так же, как на рис.3. Если для записи целой части слагаемых или суммы окажется недостаточно места, сдвиньте стрелки на минимально необходимое число разрядов вправо. Для удобства перемещения стрелок их можно сгруппировать с помощью панели «Рисование».
Варианты заданий и требования к отчету
В отчете к лабораторной работе следует дать ответы на все вопросы, приведенные в Экспериментах. Эксперимент 5 повторить с индивидуальными значениями. Отчет иллюстрировать скиншотами.
Нужно также привести исходные данные X B, Y B и результаты всех четырех шагов «программы» (1), т. е. написать в отчете числа X C, Y C, Z B, Z C, Z 10, и Z' 10 со всеми значащими цифрами, которые выдаются «машинами».
Варианты заданий к работе Таблица 1
Date: 2015-09-02; view: 5157; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |