Теорема о полноте метода резолюций для логики высказываний

Теорема. Множество дизъюнктов S противоречиво тогда и только тогда, когда существует опровержение в S (или из S).

Доказательство. Необходимость (корректность метода резолюций) очевидна, так как пустой дизъюнкт не может быть истинен ни при какой оценке. Приведём доказательство достаточности. По лемме о компактности достаточно ограничиться случаем конечного числа пропозициональных переменных. Проводим индукцию по числу пропозициональных переменных , встречающихся хотя бы в одном дизъюнкте из 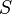. Пусть теорема полноты верна при 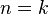, докажем ее истинность при 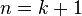. Другими словами, покажем, что из любого противоречивого множества 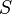дизъюнктов, в котором встречаются пропозициональные переменные 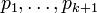, можно вывести пустой дизъюнкт.

Выберем любую из 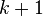пропозициональных переменных, например, 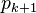. Построим по 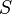два множества дизъюнктов и 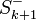. В множество поместим те дизъюнкты из 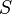, в которых не встречается литерал , причем из каждого такого дизъюнкта удалим литерал 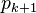(если он там встречается). Аналогично, множество 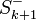содержит остатки дизъюнктов 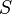, в которых не встречается литерал 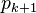, после удаления литерала (если он в них встречается).

Утверждается, что каждое из множеств дизъюнктов и 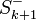является противоречивым, то есть не имеет выполняющей все дизъюнкты одновременно оценки. Это верно потому, что из оценки 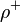, выполняющей все дизъюнкты множества одновременно, можно построить оценку 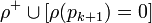, одновременно выполняющей все дизъюнкты множества 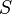. То, что эта оценка выполняет все опущенные при переходе от 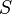к дизъюнкты, очевидно, ибо эти дизъюнкты содержат литерал . Остальные дизъюнкты 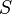выполняются по предположению, что оценка 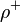выполняет все дизъюнкты множества , а, значит, и все расширенные (путем добавления выброшенного литерала 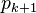). Аналогично, из оценки 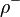, выполняющей все дизъюнкты множества 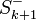одновременно, можно построить оценку 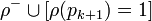, одновременно выполняющей все дизъюнкты множества .

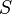По предположению индукции из противоречивых множеств дизъюнктов и 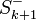(так как в каждом из них встречаются только пропозициональных переменных 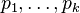) имеются выводы пустого дизъюнкта. Если мы восстановим опущенный литерал 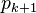для дизъюнктов множества в каждом вхождении вывода пустого дизъюнкта, то получим вывод дизъюнкта, состоящего из одного литерала 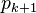. Аналогично из вывода пустого дизъюнкта из противоречивого множества 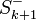получаем вывод дизъюнкта, состоящего из одного литерала . Осталось один раз применить правило резолюции, чтобы получить пустой дизъюнкт. Что и требовалось доказать.

Исчисление предикатов

Логика первого порядка (исчисление предикатов) — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высшего порядка.

Предика́т (лат. praedicatum — заявленное, упомянутое, сказанное) — это то, что утверждается о субъекте. Субъектом высказывания называется то, о чём делается утверждение

Предика́т (n -местный, или n -арный) — это функция с множеством значений (или {ложь, истина}), определённая на множестве 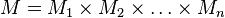. Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».

Предикат можно связать с математическим отношением: если (m₁,m₂,...,m_n) принадлежит отношению, то предикат будет возвращать на ней 1. В частности, одноместный предикат определяет отношение принадлежности некоторому множеству.

Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам.

Предикат называют тождественно-истинным и пишут:

если на любом наборе аргументов он принимает значение 1.

Предикат называют тождественно-ложным и пишут:

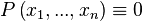
если на любом наборе аргументов он принимает значение 0.

Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1.

Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры, например: отрицание, импликация, конъюнкция, дизъюнкцияи т. д

Предикаты, так же, как высказывания, принимают два значения: истинное и ложное, поэтому к ним применимы все операции логики высказываний. Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов.

Date: 2015-09-02; view: 1089; Нарушение авторских прав