
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференциальные уравнения первого порядка с разделяющимися переменными
Определение. Дифференциальное уравнение первого порядка y' = ¦(x, y) называется уравнением с разделяющимися переменными, если его можно представить в виде:
| y ' = ¦1(x) ¦2(y). | (2.1) |
В частности, при ¦2(y) º 1 имеем простейшее уравнение
| y' = ¦(x). | (2.1а) |
Из теории неопределённого интеграла следует, что решение этого уравнения может быть записано следующим образом:
y = 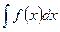 + C. + C.
| (2.2) |
Очевидно, если число а является решением уравнения ¦2(y) = 0, то функция y = a (постоянная) является решением уравнения (2.1). Для тех y, для которых ¦2(y) ¹ 0, уравнение (2.1) равносильно уравнению:
 . .
| (2.3) |
В этом уравнении переменная y присутствует только в левой части, а переменная x – в правой части. В дифференциалах уравнение (2.3) имеет вид:
 . .
| (2.3а) |
Каждая часть этого уравнения представляет собой произведение некоторого выражения, зависящего от одной переменной на дифференциал этой переменной. Его называют уравнением с разделёнными переменными.
Интегрируя почленно, получаем общее решение уравнения (2.1):
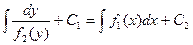 , или
, или  , где С = С 2 – С 1 –постоянная.
, где С = С 2 – С 1 –постоянная.
Итак, для нахождения решения дифференциального уравнения с разделяющимися переменными следует:
1)разделить переменные;
2) интегрируя уравнение с разделёнными переменными, найти общее решение данного уравнения;
3) выяснить, имеет ли уравнение решения, не получающиеся из общего интеграла;
4) найти частное решение, удовлетворяющее начальным условиям (если это требуется).
Пример 1. Найти все решения дифференциального уравнения y' = xy 2.
D Очевидно, что y = 0 является решением данного уравнения.
Пусть теперь y ¹ 0. Тогда 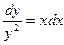 и, следовательно,
и, следовательно,
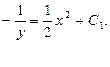
Таким образом, общее решение данного уравнения имеет вид 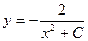 , где
, где 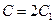 .
.  Заметим, что решение y = 0 не получается из общего решения ни при каком значении постоянной C. Ñ
Заметим, что решение y = 0 не получается из общего решения ни при каком значении постоянной C. Ñ
Пример 2. Найти частное решение уравнения y' =2 + y, если y (0) = 3.
Date: 2015-09-02; view: 496; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |