Метод интегрирования по частям

Пусть 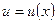и - непрерывно дифференцируемые функции. На основании формулы дифференциала произведения имеем

.

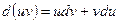Отсюда

.

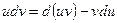Интегрируя, получим:

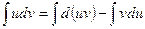или окончательно

.

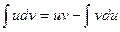(4)

Формула (4) называется формулой интегрирования по частям.

Выведенная формула показывает, что интеграл 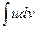приводится к интегралу 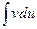, который может оказаться более простым, чем исходный, или даже табличным. Сущность метода интегрирования по частям вполне соответствует его названию. Дело в том, что при вычислении интеграла этим методом подынтегральное выражение 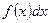представляется в виде произведения множителей u и dv. При этом dx обязательно входит в dv. В результате получается, что заданный интеграл находится по частям: сначала находим 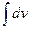, а затем .

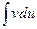Пример 1.

.

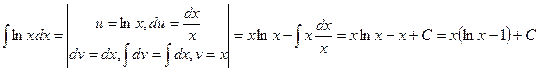В представленном примере, как и в дальнейших, вертикальными черточками отделены вспомогательные записи. Отметим также, что в качестве v можно взять любую функцию вида x+C, где С – постоянная. Мы взяли v=x, т.е. С =0.

Пример 2. .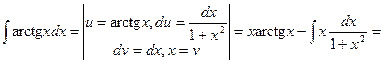

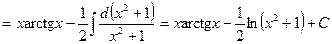Пример 3.

.

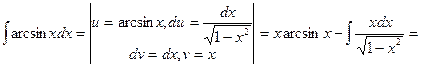
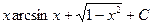Пример 4.

.

Иногда для вычисления интеграла формулу интегрирования по частям приходится применять несколько раз.

Пример 5.

.

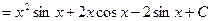Таким образом, интеграл 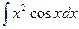вычислен двукратным интегрированием по частям.

Пример 6.

.

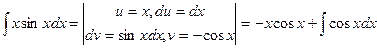
Если бы выражение u и dv мы выбрали иначе, т.е. 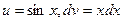, то получили бы 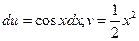, откуда 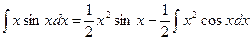, и пришли бы к интегралу более сложному, чем исходный, т.к. степень сомножителя при тригонометрической функции повысилась на единицу.

Приведенный пример показывает, что при вычислении интегралов методом интегрирования по частям главным является разумное разбиение подынтегрального выражения на множители u и dv. Общих установок по этому вопросу не имеется. Однако, для некоторых типов интегралов сделать это возможно.

а) В интегралах вида

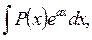
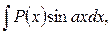
где P(х) – многочлен относительно x, а – некоторое число, полагают u=P(x), а остальные сомножители за .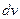

Пример 7. Найти .

D Положим , , 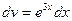тогда 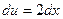, . Следовательно,

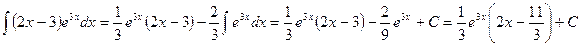Ñ

б) В интегралах вида

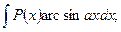
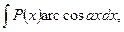
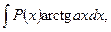
полагают 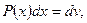а остальные сомножители – за u.

Пример 8. Найти .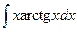

D Положим 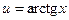, , тогда , .

Следовательно, .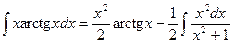

Вычислим отдельно последний интеграл:

.

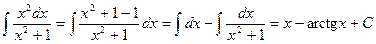Итак, 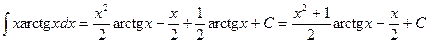. Ñ

Отметим, что на практике важно научиться применять формулу (4), не выписывая по возможности в стороне выражения для функций u и v.

Так, решение приведенного примера может быть представлено в виде:

D

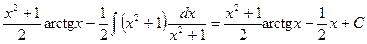= . Ñ

Возвращение к исходному интегралу

Формула интегрирования по частям применима и для нахождения интегралов вида 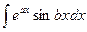и 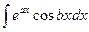, где а и b – числа. При нахождении этих интегралов она применяется последовательно два раза, причем оба раза за u выбирается либо показательная функция, либо тригонометрическая. После двукратного интегрирования по частям получается линейное уравнение относительно искомого интеграла.

Пример 9. Найти I = .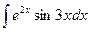

D Положим 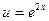, 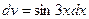. Тогда , .

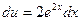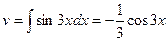Следовательно, I = .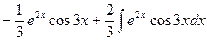

Для вычисления интеграла снова применим интегрирование по частям. Положим 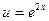, 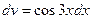. Тогда , .

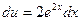Таким образом,

I= = .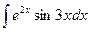

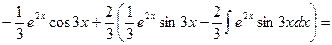
Так как в правой части стоит искомый интеграл, то, перенося его в левую часть, получим:

.

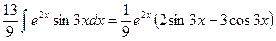Отсюда получаем окончательный результат:

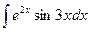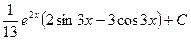= . Ñ

Применим изложенный метод к вычислению еще двух, часто используемых в приложении, интегралов.

Пример 10. Найти I = .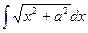

D Положим 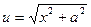, 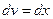. Тогда 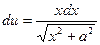, 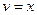. Следовательно,

(*)

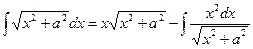
Так как 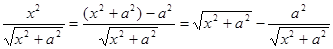, то

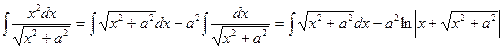
(см. лекция 2, п.2б, пример 20).

Подставив полученное выражение в равенство (*), будем иметь

.

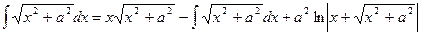Таким образом, 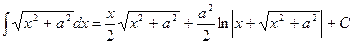. Ñ

Пример 11. Найти 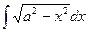, (а>0)

D Положим 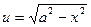, , 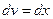откуда , 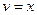. Следовательно,

,

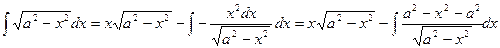или .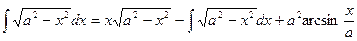

Отсюда получаем: . Ñ

Понятие о рекуррентных формулах

Иногда интегрирование по частям позволяет получить соотношение между неопределенным интегралом, содержащим степень некоторой функции, и аналогичным интегралом, но с меньшим показателем степени той же функции. Подобные соотношения называются рекуррентными формулами.

Выведем рекуррентную формулу для интеграла , где n – целое положительное число.

D При n =1 имеем табличный интеграл .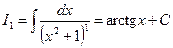

Пусть n> 1. Представив единицу в числителе как разность , получим

.

Во втором интеграле применим метод интегрирования по частям:

, , , .

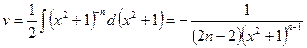Тогда 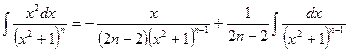. Следовательно,

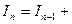
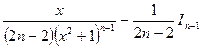, откуда .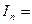

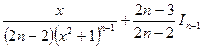Таким образом, интеграл выражен через :

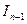(n>1). Ñ

Проверим нашу готовность приступить к интегрированию основных классов элементарных функций, вычислив интеграл 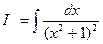, последовательно применяя методы непосредственного интегрирования, подведения функции под знак дифференциала и интегрирование по частям.

D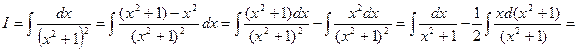

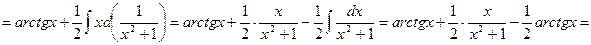
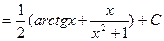. Ñ

Вычислим также интеграл

I=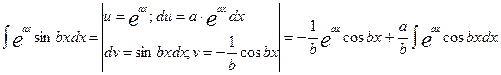

Далее полагаем u =e^ax , dv=cosbxdx, du=ae^axdx, v= 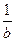sinbx. Следовательно

Получаем уравнение относительно неизвестного интеграла I. Решая его, находим

или = .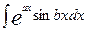

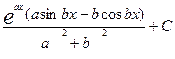* Дифференциал функции сохраняет одно и то же выражение независимо от того, является ли ее аргумент u независимой переменной или функцией от независимой переменной. Это свойство называется инвариантностью, т.е. неизменностью формы дифференциала.

Date: 2015-09-02; view: 707; Нарушение авторских прав