Основные свойства неопределенного интеграла

Лекции по основам интегрального исчисления функций одной переменной и обыкновенным дифференциальным уравнениям

Лекция 1.

Неопределенный интеграл и его свойства

1. Понятие первообразной функции и неопределенного интеграла

Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. Разнообразные вопросы математического анализа и его многочисленные приложения в геометрии, механике, физике и технике приводят к обратной задаче: по данной функции f(x) найти такую функцию F(x), производная которой была бы равна функции f(x), т.е. F'(x) = f(x). Восстановление функции по известной производной этой функции – одна из основных задач интегрального исчисления.

Определение 1. Дифференцируемая функция F(x), определенная на некотором промежутке X, называется первообразной (для, от) функции f(x), определенной на том же промежутке, если во всех точках этого промежутка выполняется равенство

или, что то же самое,

Пример 1. Функция F(x) = х ³ является первообразной функции f(x) = 3 х ² на всей числовой оси, так как при любом x (х ³)' = 3 х ² .Нетрудно заметить, что первообразная х ³ не является единственной для функции 3 х ². В самом деле, в качестве первообразной можно было бы взять и функции х ³ + 8, х ³ – 4 и, вообще, х ³+С, где С – произвольная постоянная, потому, что (х ³ +С)' = 3 х ².

Покажем, что множество функций F(x) + С, где F(x) - некоторая первообразная для функции f(x), а С – произвольная постоянная, исчерпывает все первообразные для этой функции.

Лемма.

Функция, производная которой на некотором промежутке X равна нулю, постоянна на этом промежутке.

Доказательство:

Пусть во всех точках промежутка X производная функции f(x) равна нулю, т.е f '(x) = 0. Для любых двух точек х ₁, х ₂ Î X по теореме Лагранжа получаем:

f(x2) – f(x1) = ,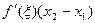

х 1<x< х 2

Так как f ' (x) = 0, то f(x₂) = f(x₁). Это и означает, что значения функции во всех точках промежутка одинаковы, т.е. f(x) = С, где С – некоторое число.

Теорема.

Если F₁(x) и F₂(x) - две первообразные для f(x) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу.

Доказательство:

Пусть, например, указанный промежуток – интервал ]а;b[. Из определения первообразной имеем: F₁'(x) = f(x) и F₂'(x) = f(x) для любого х Î ]а;b[.

Пусть a (х) = F₂(x) - F₁(x). Тогда для любого х из ]а;b[

a'(х) = F₂'(x) - F₁'(x) = f (x) – f (x) = 0.

Следовательно, согласно лемме, a (х) 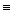С.

Подчеркнем важный факт: если производная для функции одна, т.е. операция дифференцирования однозначна, то нахождение первообразной для функции возможно лишь с точностью до некоторого постоянного слагаемого.

Определение 2. Совокупность всех первообразных для функций f(x), определенных на некотором промежутке X, называется неопределенным интегралом от функции f(x) на этом промежутке и обозначается символом 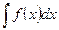(читается: "интеграл от эф от икс де икс").

Таким образом, по определению,

,

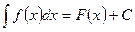(3)

если F'(x) = f(x).

Значит, чтобы найти неопределенный интеграл от заданной функции, нужно найти какую-нибудь одну ее первообразную и прибавить к ней произвольную постоянную С.

Наличие этой постоянной делает задачу нахождения функции по ее производной не вполне определенной. Отсюда происходит само название “неопределенный интеграл”.

Определение 3. Нахождение первообразной для данной функции f(x) называется интегрированием функции f(x).

Определение 4. Функция f(x) называется подынтегральной функцией, f(x)dх – подынтегральным выражением, х - переменной интегрирования, символ ∫ - знаком неопределенного интеграла, С – постоянной интегрирования.

Пример 2. Найти .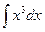

D Так как x ³ = 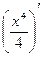, то функция F(x) = является одной из первообразных для функции f(x) = x ³. Поэтому

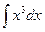= + С. Ñ

Слово “интеграл” происходит от латинского “integer”, что означает “восстановленный”. Интегрируя какую-нибудь функцию, в примере 2 функцию x³, мы как бы восстанавливаем функцию 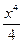, производная которой равна x³.

Определение 5. y

Назовем график какой-либо первообразной у = F(x)

функции f(x) интегральной кривой.

представляет собой семейство интегральных кривых, каждая

из которых получается из любой другой кривой

параллельным переносом вдоль оси Оу.

Отметим без доказательства, что если функция f(x) непрерывна на некотором

промежутке X, то на этом промежутке существует первообразная функции f(x), а следовательно, и неопределенный интеграл 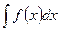(теорема Коши).

Основные свойства неопределенного интеграла

а) Производная неопределенного интеграла равна подынтегральной функции

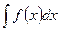()' = f(x).

Это свойство непосредственно вытекает из определения неопределенного интеграла, т. к 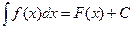, а .

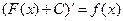D Цепочка преобразований: 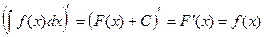. Ñ

Например, .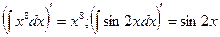

б) Дифференциал неопределенного интеграла равен подынтегральному выражению

= f(x)dx.

Это свойство также следует из определения неопределенного интеграла. Действительно, 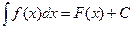,а ,

D Цепочка преобразований: . Ñ

Свойство б) означает, что знак дифференциала аннулирует знак интеграла.

Например, .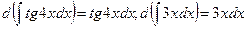

в) Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной С, т.е.

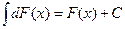или .

Действительно, dF(x)=f(x)dx. Возьмем интеграл от обеих частей равенства и получим

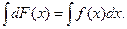Но по определению, .

D Цепочка преобразований: = = 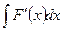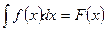+ С. Ñ

Например,

На основании этого свойства выводятся основные формулы интегрирования (см. ниже).

г) Постоянный множитель можно выносить за знак интеграла

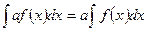
(4)

∆ Действительно, пусть F(x) – первообразная для f(x). В силу основной

формулы (3) имеем:

,

(*)

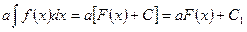где С₁ = аС, причем, С и С₁ – произвольные постоянные при а ¹ 0. Но аF(x) есть первообразная для функции аf(x), так как а [ F(x) ]' = аF'(x) = аf(x). Поэтому из формулы (*) получаем требуемую формулу (4). Ñ

Коротко запишем: .

Действительно, производные обеих частей равенства равны:

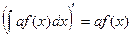и .

д) Неопределенный интеграл от алгебраической суммы двух непрерывных функций равен алгебраической сумме интегралов от этих функций в отдельности, т.е.

.

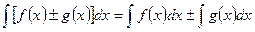(5)

D В самом деле, пусть F'(x) = f(x) и G'(x) = g(x).

Тогда и .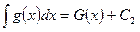

Поэтому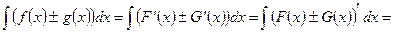

= , где С₁+С₂=С. Ñ

Здесь был использован тот факт, что производная алгебраической суммы функций равна алгебраической сумме производных этих функций и свойство а) неопределенного интеграла.