Евклидово пространство

- конечномерное векторное пространство с положительно определённым скалярным произведением. Является непосредств. обобщением обычного трёхмерного пространства. В Е. п. существуют декартовы координаты, в к-рых скалярное произведение (ху)векторов х- (x ₁ ,..., х _n)и y = (y ₁,..., y _п)имеет вид (xy)=x ₁ y ₁ +...+х _n у _п. В произвольных координатах скалярное произведение по определению удовлетворяет условиям: 1) (хх)/0, (хх) = 0лишь при x =0; 2) (ху) = (ух)*; 3) (a ху) = a(ху); 4) (x { y+ z}) =(xy)+ (xz), где a - любое комплексное число, * означает комплексное сопряжение. В Е. п. имеет место неравенство Коши - Буняковского | xу |²[(хх)(уу). Число

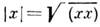
наз. нормой (или длиной)вектора х, а угол q между векторами х, у находят из ф-лы cosq= (xy)/|x| |у|. Первоначально евклидовыми наз. пространства, в к-рых выполнены аксиомы евклидовой геометрии, осн. понятиями к-рой являются длина векторов и угол между ними. Бесконечномерное Е. п. обычно наз. гильбертовым пространством. Пространство, в к-ром нарушено условие 1) положительности скалярного произведения, наз. псевдоевклидовым пространством. Пространство, в к-ром п четно, а условие 2) заменяется условием (ху) = --(ух), наз. симплектическим пространством. Лит.: Гельфанд И. М., Лекции по линейной алгебре, 4 изд., М., 1971; Дубровин Б. А., Новиков С. П., Фоменко А. Т., Современная геометрия, 2 изд., М., 1986. С. В. Молодцов.

24.Ортогональный базис — базис, составленный из попарно ортогональных векторов.

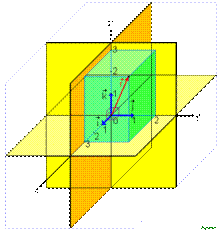
Ортонормированный базис в 3-мерном евклидовом пространстве

Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами.

Последнее удобно записывается при помощи символа Кронекера:

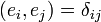
то есть скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают (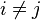), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.

Очень многое записывается в ортогональном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности.

Ортонормированный базис является самодуальным (дуальный ему базис совпадает с ним самим). Поэтому в нём можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы).

Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически.

Коэффициенты в разложении вектора по ортогональному базису:

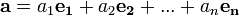
можно найти так:

.

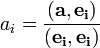Полнота ортонормированной системы векторов эквивалентна равенству Парсеваля: для любого вектора 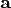квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:

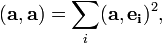
Аналогичные соотношения имеют место и для бесконечномерного случая (см. ниже).

Date: 2015-08-24; view: 524; Нарушение авторских прав