Третий шаг

Теперь необходимо понять, какая простая переменная первой обратится в ноль по мере увеличения входящей переменной. Для этого достаточно рассмотреть систему:

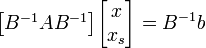
При фиксированных значениях непростых переменных система однозначно разрешима относительно простых, поэтому мы можем определить, какая из простых переменных первой достигнет нуля при увеличении входящей. Эту переменную назовем выходящей. Это будет означать, что мы натолкнулись на новую вершину. Теперь входящую и выходящую переменную поменяем местами — входящая «войдёт» в простую, а выходящая из них «выйдет» в непростые. Теперь перепишем матрицу B и вектор c_B в соответствии с новыми наборами простых и непростых переменных, после чего вернёмся ко второму шагу. x''

Поскольку число вершин конечно, то алгоритм однажды закончится. Найденная вершина будет являться оптимальным решением.

4. Программа

#include <stdio.h>

#include <math.h>

#include <stdlib.h>

const double eps = 0.00001;

const int size = 100;

double* tab;

double* tab2;

int* Pos;

double X[10000];

int N[100];

int B[100];

double* vect;

double* vect2;

double* c;

double* c2;

int Ncount = 0;

int Bcount = 0;

int n = 0, m = 0;

void initAll ()

{

int i;

for (i = 0; i < 100; i++)

{

N[i] = 0;

B[i] = 0;

}

for (i = 0; i < 10000; i++)

X[i] = 0;

Ncount = 0;

Bcount = 0;

}

void initTable (double* tab, int sz)

{

int i,j;

for (i = 0; i < sz; i++)

for (j = 0; j < sz; j++)

tab[ i*size+j ] = 0;

}

void initVector (double* v, int sz)

{

int i;

for (i = 0; i < sz; i++)

v[i] = 0;

}

void printTable (double* table, int n, int m)

{

int i,j;

for (i = 0; i < m+n; i++)

{

for (j = 0; j < n+m; j++)

printf ("%2lg ", table[i*size+j]);

printf ("\n");

}

printf ("\n");

}

void printVector_d (double* v, int num)

{

int i;

for (i = 0; i < num; i++)

printf("%lg ", v[i]);

printf("\n");

}

void printVector_i (int* v, int num)

{

int i;

for (i = 0; i < num; i++)

printf("%d ", v[i]);

printf("\n");

}

void printSystem ()

{

printf("system P_i,j:\n");

printTable (tab, n,m);

printf("right part T_j:\n");

printVector_d (vect, n+m);

printf("\nb_j:\n");

printVector_d (c, n+m);

printf("\nsupportive arrays:\n");

printVector_i (B, Bcount);

printVector_i (N, Ncount);

}

void loadTable (FILE *in)

{

int i,j;

if (in == NULL) printf ("error openning file");

else

{

initAll ();

fscanf(in, "%d %d", &n, &m);

tab = new double[size*size];

tab2 = new double[size*size];

vect = new double[n+m+2];

vect2 = new double[n+m+2];

c = new double[n+m+2];

c2 = new double[n+m+2];

initVector (vect, n+m);

initVector (c, n+m);

initTable (tab, n+m);

i = 0;

while (i < m)

{

j = 0;

while (j < n)

{

fscanf(in, "%lg", &tab[(i+n)*size+j]);

j++;

}

fscanf(in, "%lg", &vect[i+n]);

i++;

}

i = 0;

while (i < n)

{

fscanf(in, "%lg", &c[i]);

i++;

}

i = 0;

while (i < n)

{

N[Ncount] = i;

Ncount++;

i++;

}

while (i < n+m)

{

B[Bcount] = i;

Bcount++;

i++;

}

}

}

void procVectors (int l, int e)

{

initVector (vect2, n+m);

initVector (c2, n+m);

initTable (tab2, n+m);

int i,j;

vect2[e] = vect[l]/tab[l*size+e];

for (i = 0; i < Ncount; i++)

if (N[i] == e)

continue;

else

tab2[e*size+N[i]] = tab[l*size+N[i]]/tab[l*size+e];

tab2[e*size+l] = 1. / tab[l*size+e];

for (i = 0; i < Bcount; i++)

if (B[i] == l)

continue;

else

{

vect2[B[i]] = vect[B[i]] - tab[B[i]*size+e]*vect2[e];

for (j = 0; j < Ncount; j++)

if (N[j] == e)

continue;

else

tab2[B[i]*size + N[j]] = tab[B[i]*size + N[j]] - tab[B[i]*size + e]*tab2[e*size + N[j]];

tab2[B[i]*size + l] = - tab[B[i]*size + e]*tab2[e*size + l];

}

for (i = 0; i < Ncount; i++)

if (N[i]==e)

continue;

else c2[N[i]] = c[N[i]] - c[e]*tab2[e*size + N[i]];

c2[l] = -c[e] * tab2[e*size + l];

for (i = 0; i < Ncount; i++)

if (N[i] == e)

break;

for (j = 0; j < Bcount; j++)

if (B[j] == l)

break;

B[j] = e;

N[i] = l;

double* tmp;

tmp = tab;

tab = tab2;

tab2 = tmp;

tmp = vect;

vect = vect2;

vect2 = tmp;

tmp = c;

c = c2;

c2 = tmp;

}

int simplexMethod ()

{

int i,j,e,l, tmp;

bool flag = true;

flag = false;

for (j = 0; j < Ncount; j++)

if (c[N[j]] > 0)

{

flag = true;

e = N[j];

}

while (flag)

{

l = -1;

for (i = 0; i < Bcount; i++)

{

if (tab[B[i]*size+e] > 0)

if (l < 0)

l = B[i];

else if (vect[B[i]]/tab[B[i]*size+e] < vect[l]/tab[l*size+e])

l = B[i];

}

if (l < 0)

return -1;

procVectors(l,e);

flag = 0;

for (j = 0; j < Ncount; j++)

if (c[N[j]] > 0)

{

flag = 1;

e = N[j];

}

}

return 0;

}

int initSimplex ()

{

int i,j,k,e,l;

k = 0;

for (i = 0; i < n+m; i++)

if (vect[i] < vect[k])

k = i;

if (vect[k] >= 0)

return 0;

double* cs = c;

c = new double[n+m+1];

initVector (c, n+m+1);

for (i = 0; i < Bcount; i++)

tab[B[i]*size + n+m] = -1;

c[n+m] = -1;

N[Ncount] = n+m;

Ncount++;

l = k;

n++;

procVectors(l, n+m-1);

simplexMethod ();

n--;

for (i = 0; i < Bcount; i++)

if (B[i] == n+m)

return -1;

for (i = 0; i < Ncount; i++)

if (N[i] == n+m)

break;

N[i] = N[Ncount - 1];

Ncount--;

initVector (c,n+m);

for (i = 0; i < n+m; i++)

{

for (j = 0; j < Bcount; j++)

if (B[j] == i)

break;

if (j < Bcount)

for (k = 0; k < n+m; k++)

c[k] -= cs[i] * tab[B[j]*size+k];

else

c[i] += cs[i];

}

return 0;

}

int solve ()

{

if (initSimplex () < 0)

return -1;

simplexMethod();

int i;

for (i = 0; i < Ncount; i++)

X[N [i]] = 0;

for (i = 0; i < Bcount; i++)

X[B[i]] = vect[B[i]];

printf ("\nsolution X_j:\n");

for (i = 0; i < n; i++)

printf ("%lg ", X[i]);

printf ("\n");

return 0;

}

int main (void)

{

FILE *in = fopen("input1.txt", "r+");

loadTable (in);

printSystem ();

solve ();

return 0;

}

5. Результаты

n = 3 m = 3

P_ij:

0.3 0.7 0.2 1

0.3 0.8 0.2 1

0.3 0.5 0.4 1

b₁ = 0.4 b₂ = 2 b₃ = 0.5

Ответ: X₁ = 0, X₂ = 0.909, X₃ = 1.363

6. Вывод

Наиболее известным и широко применяемым на практике для решения общей задачи линейного программирования (ЛП) является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом с экспоненциальной сложностью. Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранника допустимых решений при поиске оптимального решения.

Первый полиномиальный алгоритм, метод эллипсоидов, был предложен в 1979 году советским математиком Л. Хачияном, разрешив таким образом проблему, долгое время остававшуюся нерешённой. Метод эллипсоидов имеет совершенно другую, некомбинаторную, природу, нежели симплекс-метод. Однако в вычислительном плане этот метод оказался неперспективным. Тем не менее, сам факт полиномиальной сложности задач привёл к созданию целого класса эффективных алгоритмов ЛП — методов внутренней точки, первым из которых был алгоритм Н. Кармаркара, предложенный в 1984 году. Алгоритмы этого типа используют непрерывную трактовку задачи ЛП, когда вместо перебора вершин многогранника решений задачи ЛП осуществляется поиск вдоль траекторий в пространстве переменных задачи, не проходящих через вершины многогранника. Метод внутренних точек, который, в отличие от симплекс-метода, обходит точки из внутренней части области допустимых значений, использует методы логарифмических барьерных функций нелинейного программирования, разработанные в 1960-х годах Фиако (Fiacco) и МакКормиком (McCormick).