
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Вказівки до виконання контрольної роботи ( РГР )
1.1.1 Невизначений інтеграл.
Функція 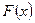 називається первісною для функції
називається первісною для функції 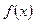 на проміжку
на проміжку 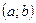 , якщо
, якщо 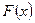 диференційована на
диференційована на 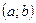 і справджується рівність
і справджується рівність 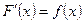 для усіх
для усіх 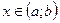 . Існує множина первісних
. Існує множина первісних 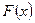 для функції
для функції 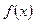 , які відрізняються тільки сталою:
, які відрізняються тільки сталою: 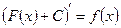 . Цю множину первісних називають невизначеним інтегралом функції
. Цю множину первісних називають невизначеним інтегралом функції 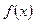 і записують
і записують 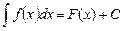 , де
, де 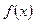 – підінтегральна функція.
– підінтегральна функція.
Властивості невизначеного інтеграла
а) 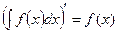
б) 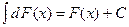
в) 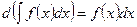
г) 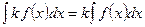 , де
, де 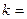 const
const
д) 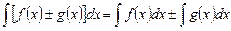
е) 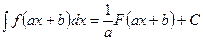
Таблиця невизначених інтегралів 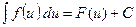

| 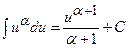 ; ; 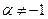
| ||
| 2a | 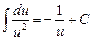
| 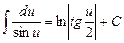
| |
| 2б | 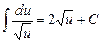
| 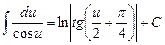
| |
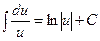
| 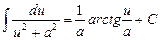
| ||
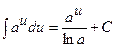
| 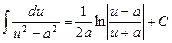
| ||
| 4а | 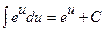
| 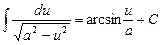
| |
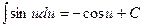
| 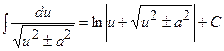
| ||

| 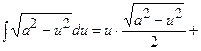 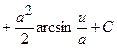
| ||
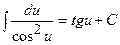
| 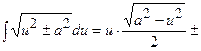 
| ||
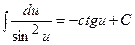
| 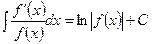
| ||
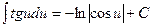
| 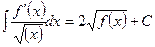
| ||
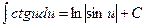
|
Зауваження: таблицею інтегралів можна користуватись у випадку, коли аргумент підінтегральної функції і вираз під знаком диференціала однакові.
Методи інтегрування
а) метод безпосереднього інтегрування. Обчислення інтегралів за допомогою властивостей невизначеного інтеграла та таблиці невизначених інтегралів.
Треба пам’ятати, що 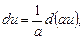
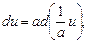
 , де
, де 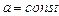 .
.
Задача 1. Знайти інтеграли
1) 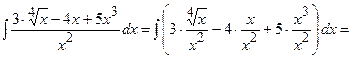
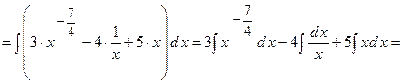
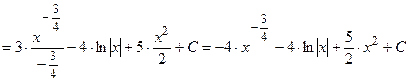 ;
;
2) 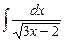 . Можемо застосувати формулу 2б, де
. Можемо застосувати формулу 2б, де  , і врахуємо лінійність аргументу u. За властивістю е) коефіцієнт лінійності дорівнює 3. Матимемо:
, і врахуємо лінійність аргументу u. За властивістю е) коефіцієнт лінійності дорівнює 3. Матимемо: 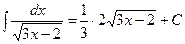 ;
;
3) 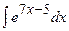 . Аналогічно прикладу 2), коефіцієнт лінійності дорівнює 7. Застосовуємо формулу 4а. Матимемо:
. Аналогічно прикладу 2), коефіцієнт лінійності дорівнює 7. Застосовуємо формулу 4а. Матимемо:
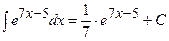 ;
;
4) 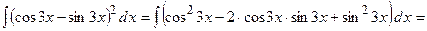
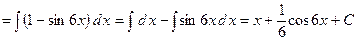 .
.
При знаходженні інтеграла врахували, що 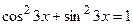 і
і 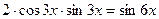
б) метод заміни змінної (метод підстановки). Згідно цього метода вводять нову змінну інтегрування. Нехай 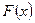 – первісна функції
– первісна функції 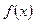 на проміжку
на проміжку 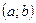 . Функція
. Функція 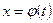 визначена та диференційована на проміжку
визначена та диференційована на проміжку 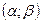 і
і 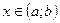 . Тоді справедлива формула
. Тоді справедлива формула 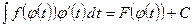 . Зручним є і такий запис:
. Зручним є і такий запис:  Підстановку
Підстановку 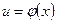 підбирають так, щоб мати після перетворення табличний інтеграл.
підбирають так, щоб мати після перетворення табличний інтеграл.
Задача 2. Знайти інтеграли
1) 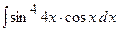
Так як  , то зробимо заміну змінної
, то зробимо заміну змінної 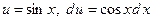 . Матимемо:
. Матимемо:
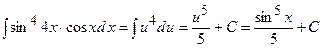 . Перевіримо отриманий результат:
. Перевіримо отриманий результат:
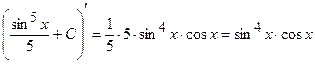 .
.
2)  =
=

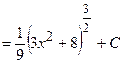 .
.
3) 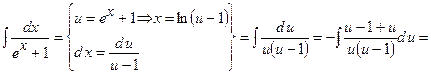

в) метод інтегрування частинами. Формула інтегрування частинами має вигляд: 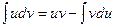 . До інтегралів, які обчислюються методом інтегрування частинами відносяться:
. До інтегралів, які обчислюються методом інтегрування частинами відносяться:
1) 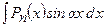 ,
, 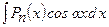 ,
, 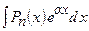 ,
, 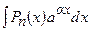 , де
, де  – многочлен
– многочлен 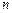 -го степеня,
-го степеня,  – дійсне число. В цих інтегралах через
– дійсне число. В цих інтегралах через 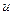 позначаємо
позначаємо  , а через
, а через 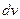 – один з виразів
– один з виразів 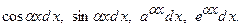
2) 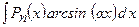 ,
, 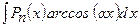 ,
, 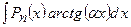 ,
, 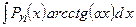 ,
, 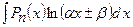 ,
, 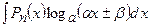 , де
, де  – многочлен
– многочлен 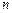 -го степеня (
-го степеня (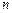 може дорівнювати нулю),
може дорівнювати нулю), 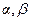 – дійсні числа. В цих інтегралах через
– дійсні числа. В цих інтегралах через 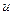 позначаємо один з виразів
позначаємо один з виразів 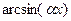 ,
, 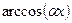 ,
, 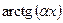 ,
, 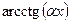 ,
,  ,
,  , а через
, а через 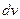 –
– 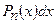 .
.
Існують інші типи інтегралів для знаходження яких застосовують метод інтегрування частинами.
Зауваження. При застосуванні метода інтегрування частинами треба підінтегральний вираз розбити на два множники: u і 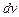 , а саме: 1)
, а саме: 1) 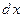 треба віднести до
треба віднести до 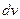 ; 2)
; 2) 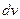 повинен бути таким, щоб інтегруванням легко знайти
повинен бути таким, щоб інтегруванням легко знайти 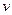 ; 3) Інколи доводиться формулу інтегрування частинами застосовувати декілька разів.
; 3) Інколи доводиться формулу інтегрування частинами застосовувати декілька разів.
Задача 3. Знайти інтеграли
1) 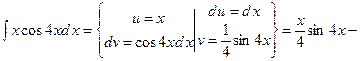
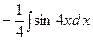
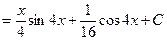 ;
;
2) 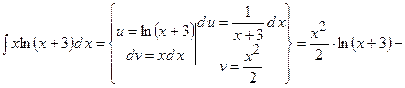
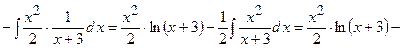

3) 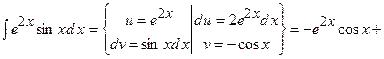
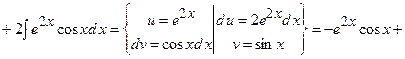
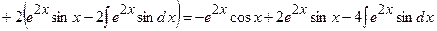
Розв’яжемо отримане рівняння відносно шуканого інтеграла
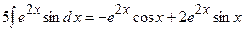
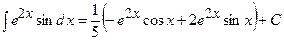
г) інтегрування квадратних тричленів. До цих інтегралів відносяться:
1)  , 2)
, 2)  , 3)
, 3) 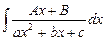 ,
,
4) 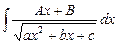 . Для інтегралів 1), 2) типів необхідно виділити повний квадрат у квадратному тричлені:
. Для інтегралів 1), 2) типів необхідно виділити повний квадрат у квадратному тричлені:
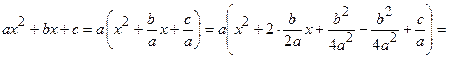
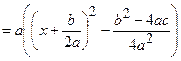 . Заміна
. Заміна  приводить інтеграл до табличного: для інтеграла 1) типу маємо табличний інтеграл 13 або 14, для інтеграла 2) типу маємо табличний інтеграл 15 або 16. Для інтегралів 3), 4) типів необхідно у чисельнику виділити похідну квадратного тричлена, який знаходиться у знаменнику, і чисельник почленно поділити на знаменник. Отримаємо два інтеграли, перший з яких знаходимо по таблиці інтегралів за формулою 17 (для інтеграла 3) типу) або 18 (для інтеграла 4) типу). Другий інтеграл є інтегралом 1) або 2) типу.
приводить інтеграл до табличного: для інтеграла 1) типу маємо табличний інтеграл 13 або 14, для інтеграла 2) типу маємо табличний інтеграл 15 або 16. Для інтегралів 3), 4) типів необхідно у чисельнику виділити похідну квадратного тричлена, який знаходиться у знаменнику, і чисельник почленно поділити на знаменник. Отримаємо два інтеграли, перший з яких знаходимо по таблиці інтегралів за формулою 17 (для інтеграла 3) типу) або 18 (для інтеграла 4) типу). Другий інтеграл є інтегралом 1) або 2) типу.
Задача 4. Знайти інтеграл
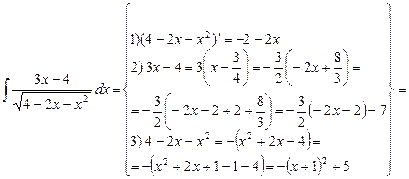
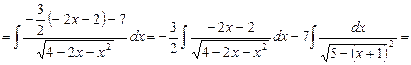
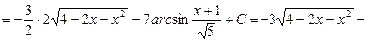
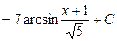
д) інтегрування дробово-раціональних функцій. До цих функцій
відносяться дроби 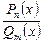 . Якщо
. Якщо 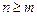 , то дріб є неправильний. Треба виділити цілу частину, поділивши чисельник на знаменник:
, то дріб є неправильний. Треба виділити цілу частину, поділивши чисельник на знаменник: 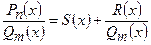 , де
, де 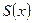 – частка (ціла частина),
– частка (ціла частина),  – правильний дріб (степінь многочлена
– правильний дріб (степінь многочлена 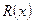 менший за
менший за 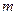 ). Далі, якщо правильний дріб не є простий, необхідно знаменник
). Далі, якщо правильний дріб не є простий, необхідно знаменник 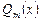 розкласти на множники (множниками можуть бути многочлени виду:
розкласти на множники (множниками можуть бути многочлени виду: 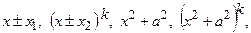
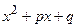 ,
, 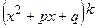 з дискримінантом квадратного тричлена меншим нуля), потім правильний дріб – на прості дроби. Простих дробів буде стільки, скільки множників у знаменнику, враховуючи кратність кожного. У чисельниках простих дробів записують многочлени в загальному вигляді, не враховуючи кратність многочленів у знаменнику. Коефіцієнти чисельників знаходимо методом невизначених коефіцієнтів або комбінованим методом. При інтегруванні правильних простих дробів можемо мати такі інтеграли:
з дискримінантом квадратного тричлена меншим нуля), потім правильний дріб – на прості дроби. Простих дробів буде стільки, скільки множників у знаменнику, враховуючи кратність кожного. У чисельниках простих дробів записують многочлени в загальному вигляді, не враховуючи кратність многочленів у знаменнику. Коефіцієнти чисельників знаходимо методом невизначених коефіцієнтів або комбінованим методом. При інтегруванні правильних простих дробів можемо мати такі інтеграли:
 ;
;
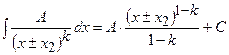 ;
;
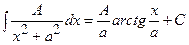 ;
;
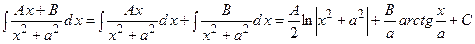
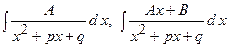 – розглянуті в інтегруванні квадратних тричленів;
– розглянуті в інтегруванні квадратних тричленів;
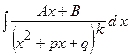

 , де
, де 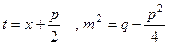 . При цьому многочлен
. При цьому многочлен 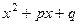 немає дійсних коренів, тобто
немає дійсних коренів, тобто 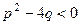 ;
;
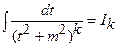 можна знайти використовуючи рекурентну формулу:
можна знайти використовуючи рекурентну формулу: 
Задача 5. Знайти інтеграли
1) 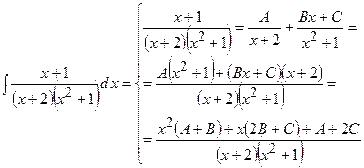
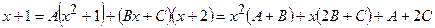
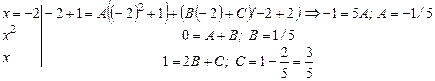
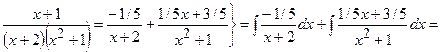
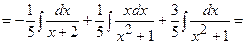
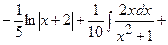
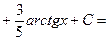
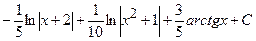 ;
;
2) 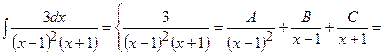
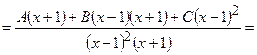
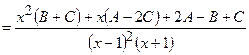
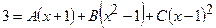 =
= 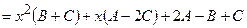
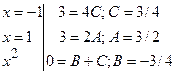
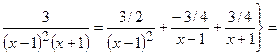
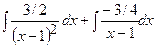 +
+
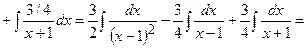
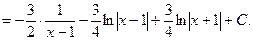
е) інтегрування тригонометричних функцій. Інтеграли виду 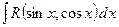 за допомогою універсальної підстановки
за допомогою універсальної підстановки 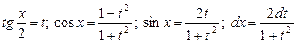 приводяться до інтегралів від раціональних дробів. В деяких випадках застосовують інші підстановки, які спрощують знаходження інтегралів. Розглянемо ці випадки.
приводяться до інтегралів від раціональних дробів. В деяких випадках застосовують інші підстановки, які спрощують знаходження інтегралів. Розглянемо ці випадки.
1) у випадку коли функція 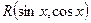 непарна відносно
непарна відносно 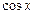 :
:  , робимо заміну
, робимо заміну 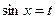 , а коли вона непарна відносно
, а коли вона непарна відносно 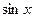 :
: 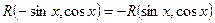 , то робимо заміну
, то робимо заміну 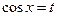 .
.
2) якщо функція 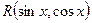 парна відносно
парна відносно 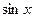 і
і  :
: 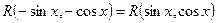 , то робимо заміну
, то робимо заміну

3) 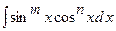 знаходиться підстановкою
знаходиться підстановкою 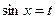 , якщо
, якщо 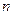 – ціле додатне непарне число, а
– ціле додатне непарне число, а 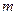 – ціле додатне парне число, або підстановкою
– ціле додатне парне число, або підстановкою 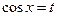 , якщо
, якщо 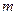 – ціле додатне непарне число, а
– ціле додатне непарне число, а 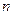 – ціле додатне парне число. У випадку, коли
– ціле додатне парне число. У випадку, коли 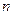 і
і 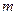 – цілі додатні парні числа, застосовують формули зниження степеня
– цілі додатні парні числа, застосовують формули зниження степеня  ,
, 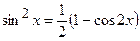 та
та 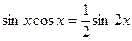 . Якщо
. Якщо 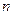 і
і 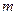 – цілі парні числа, але хоч одне з них від’ємне, або
– цілі парні числа, але хоч одне з них від’ємне, або 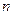 і
і 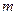 – цілі непарні і від’ємні числа, то застосовують підстановку
– цілі непарні і від’ємні числа, то застосовують підстановку 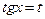 .
.
4)  за допомогою формул:
за допомогою формул:
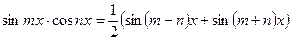 ;
;
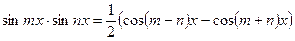 ;
;
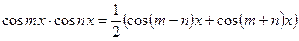
зводяться до табличних.
Задача 6. Знайти інтеграли.
1) 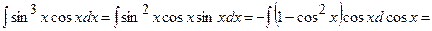

2) 
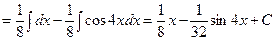
3) 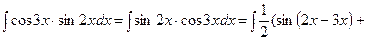
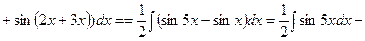
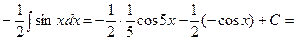
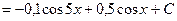
4) 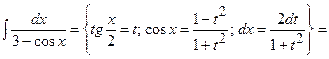
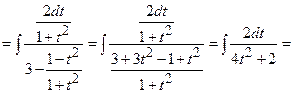
 =
=

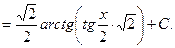
є) інтегрування ірраціональних виразів. Розглянемо деякі з них.
1) 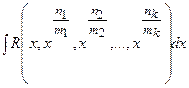 , де
, де 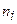 ,
, 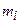
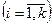 – цілі додатні числа. Робимо заміну
– цілі додатні числа. Робимо заміну 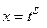 , де
, де 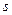 є спільним знаменником дробів
є спільним знаменником дробів  . Ця заміна приводить до інтегралу від раціональної функції аргументу
. Ця заміна приводить до інтегралу від раціональної функції аргументу 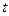 .
.
2) 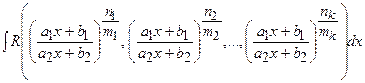 , де
, де 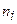 ,
, 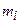
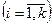 – цілі додатні числа,
– цілі додатні числа, 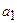 ,
, 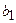 ,
, 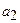 ,
, 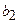 – дійсні числа. Заміна:
– дійсні числа. Заміна: 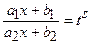 , де
, де 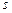 є спільним знаменником дробів
є спільним знаменником дробів 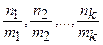 . Ця заміна приводить до інтегралу від раціональної функції аргументу
. Ця заміна приводить до інтегралу від раціональної функції аргументу 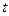 .
.
3) В інтегралах, що мають вирази: 3а) 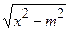 , 3б)
, 3б) 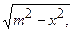
3в)  можна робити наступні заміни змінної:
можна робити наступні заміни змінної:
3а) 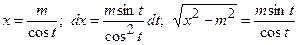
3б) 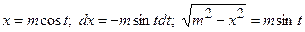
3в) 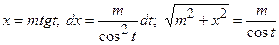
Задача 7. Знайти інтеграл.
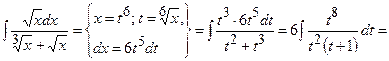

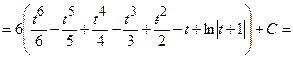
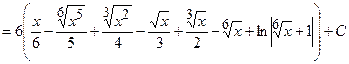
1.1.2 Визначений інтеграл.
Визначений інтеграл 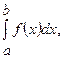 де функція
де функція 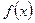 неперервна на відрізку інтегрування
неперервна на відрізку інтегрування  ,
, 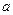 – нижня межа інтегрування,
– нижня межа інтегрування,  – верхня межа інтегрування, обчислюється за формулою Ньютона-Лейбніца:
– верхня межа інтегрування, обчислюється за формулою Ньютона-Лейбніца:
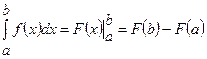 , де
, де 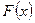 є первісною для підінтегральної функції
є первісною для підінтегральної функції 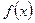 .
.
Властивості визначеного інтеграла
а) 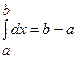
б) 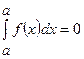
в) 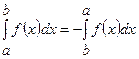
г)  ,
, 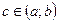
д) 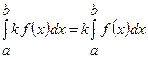 , де
, де 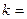 const
const
е) 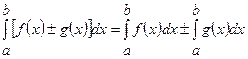
є) якщо відрізок інтегрування симетричний: 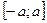 , то для парної підінтегральної функції
, то для парної підінтегральної функції 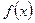
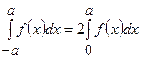 , для непарної функції
, для непарної функції  .
.
Для знаходження первісної 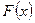 при обчисленні визначеного інтеграла можна застосувати табличні інтеграли та методи інтегрування для обчислення невизначених інтегралів. Розглянемо деякі з них.
при обчисленні визначеного інтеграла можна застосувати табличні інтеграли та методи інтегрування для обчислення невизначених інтегралів. Розглянемо деякі з них.
а) заміна змінної під знаком визначеного інтеграла. Якщо функції 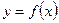 і
і  задовольняють умовам: функція
задовольняють умовам: функція 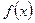 неперервна на
неперервна на  ; функція
; функція 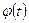 має неперервну похідну
має неперервну похідну  на
на 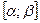
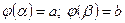 ; складена функція
; складена функція  визначена і неперервна на
визначена і неперервна на 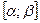 , то
, то 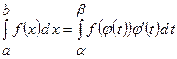 .
.
б) формула інтегрування частинами у визначеному інтегралі
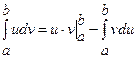 .
.
Задача 8. Знайти інтеграли.
1) 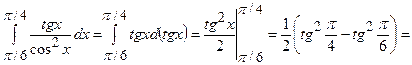
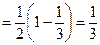 ;
;
2) 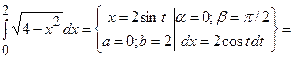


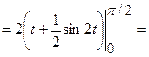
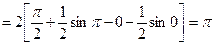 ;
;
3) 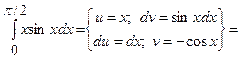
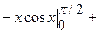
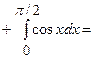
Date: 2015-08-24; view: 321; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |