Теорема 1.14

1. Размерность корневого подпространства матрицы , соответствующего собственному числу 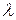, совпадает с кратностью .

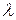2. В каждом корневом подпространстве существует цепной базис.

3. Количество цепей фиксированной длины в произвольных двух цепных базисах одного и того же корневого подпространства одинаково.

4. Количество цепей в произвольном цепном базисе корневого подпространства матрицы , соответствующего собственному числу 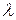, равно размерности соответствующего собственного подпространства.

5. Количество цепей длины не меньше чем в произвольном цепном базисе корневого подпространства матрицы , соответствующего собственному числу 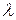, равно разности дефектов матриц 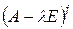и .

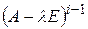Теорема 1.15 Для матрицы 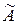линейного оператора существует жорданов базис, в котором матрица линейного оператора является жордановой матрицей: 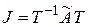, где 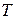– матрица перехода. В этом случае матрица J называется жордановой нормальной формойматрицы 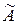. Жорданова нормальная форма матрицы определена однозначно с точностью до порядка жордановых клеток на диагонали.

Алгоритм нахождения жордановой нормальной формы квадратной матрицы порядка :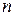

1. Найти собственные значения матрицы 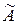и их кратности.

2. Если собственное значение единственное, то вычислить число всех жордановых клеток, соответствующих собственному значению λ по формуле

.

Если собственных значений несколько, то для каждого собственного значения 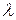матрицы и для каждого 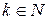найти количество 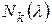жордановых клеток 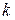-го порядка, соответствующих собственному значению λ. Для этого вычислить числа 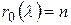, , 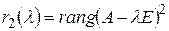и так далее до тех пор, пока для некоторого 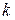не будет выполнено равенство равно 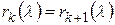. После этого воспользоваться формулой

.

3. Построить жорданову нормальную форму матрицы как блочно-диагональную матрицу, диагонали которой составляют найденные жордановы клетки. Следует обратить внимание, что в полученной матрице собственное значение должно встречаться на диагонали столько раз, какова его кратность.

4. Для нахождения жорданова базиса, в котором матрица линейного оператора является жордановой матрицей, нужно

І способ: найти матрицу перехода 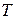, решив относительно 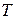матричное уравнение: 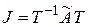, то есть .

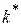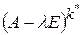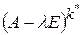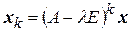ІІ способ: в пункте 3 зафиксировать то наименьшее , для которого , и найти базис ядра матрицы , решив однородную СЛАУ с матрицей . Для каждого полученного базисного вектора построить цепь . Выбрать 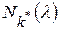цепей наибольшей длины, состоящих из линейно независимых элементов, – это часть искомого базиса. Проделать аналогичные действия для следующего (по убыванию) 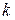, для которого , следя за линейной независимостью выбираемых векторов и выбранными раньше. Продолжать до тех пор, пока не будут выбраны все цепи. Составляем матрицу перехода 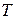соответственно жордановой форме следующим образом: слева направо в матрице 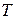по столбцам выписать координаты соответствующих базисных векторов в такой последовательности: сначала – собственный вектор, потом – следующий за ним вектор цепи и так далее. Тоже проделать для второй жордановой клетки, третей и так далее.

Пример Найти жорданову нормальную форму матрицы:

.

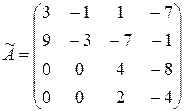Решение. Составим характеристическое уравнение и найдем его корни, т.е. собственные значения:

.

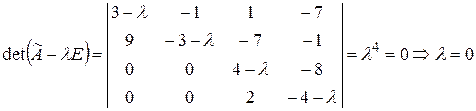Число всех жордановых клеток, соответствующих собственному значению , равно:

.

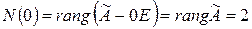Число жордановых клеток 1-го порядка, соответствующих собственному значению , равно

,

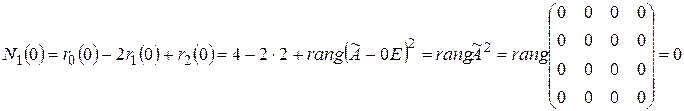т.е. жорданова нормальная форма не содержит клеток 1-го порядка, соответствующих собственному значению .

Порядок матрицы 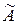равен 4, всего 2 жордановых клетки и нет клеток 1-го порядка. Поэтому жорданова нормальная форма матрицы содержит только две жордановых клетки 2-го порядка (4=2+2):

.

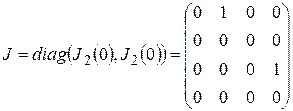Пример Определить жорданову нормальную форму 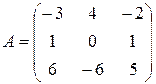и жорданов базис.

Решение. Характеристическое уравнение , т.е.

.

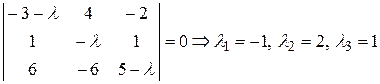Так как порядок матрицы равен 3, а число собственных значений также равно 3, то жорданова нормальная форма .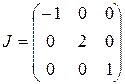

Найдем жорданов базис. Так как собственные значения все разные и их количество равно рангу матрицы, то за базис можно взять собственное подпространство (систему собственных векторов): 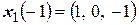, , 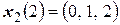. Тогда

.

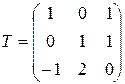1.7 Инвариантные подпространства

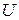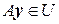Подпространство пространства называется инвариантным подпространством линейного оператора , если и вектор . Это значит, что линейный оператор любой вектор инвариантного подпространства переводит в некоторый вектор этого же подпространства. Можно сказать, что все инвариантное подпространство линейным оператором переводится в себя. Это обычно записывается формулой .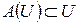

Нулевое подпространство и все пространство являются инвариантными для любого линейного оператора. Не всякое подпространство, инвариантное для одного линейного оператора, будет инвариантным и для другого. Если спектр линейного оператора не пуст, то линейная оболочка, порожденная любым собственным вектором, является инвариантным одномерным подпространством. И наоборот, любое одномерное инвариантное подпространство состоит из собственных векторов и нулевого вектора. Линейная оболочка является инвариантным подпространством линейного оператора тогда и только тогда, когда векторы . Сумма и пересечение инвариантных подпространств являются инвариантными подпространствами этого линейного оператора. Любое подпространство, содержащееся в ядре , и любое подпространство, содержащее образ , являются инвариантными подпространствами линейного оператора .

Пусть 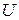является инвариантным подпространством линейного оператора . Тогда линейный оператор называется индуцированным, если .

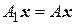1.8 Минимальный многочлен

Ненулевой многочлен

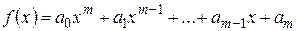
называется аннулирующим многочленом линейного оператора , если линейный оператор 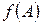является нулевым:

.

Для любого линейного оператора его множество аннулирующих многочленов непусто. В частности характеристический многочлен линейного оператора является его аннулирующим многочленом: .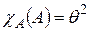

Минимальным многочленом линейного оператора называется его аннулирующий многочлен наименьшей степени с равным единице старшим коэффициентом. Для любого линейного оператора существует его минимальный многочлен. Этот многочлен единственен и все аннулирующие многочлены линейного оператора делятся на его минимальный многочлен.

Если характеристический многочлен над полем 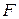имеет каноническое разложение

,

где при 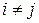, , то минимальный многочлен имеет вид

, .

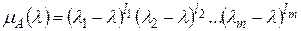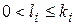Натуральные числа равны наибольшему порядку жордановых клеток с собственным значением , , на диагонали для данной матрицы. А значит, эти числа удовлетворяют следующим соотношениям

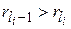и ,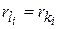

где 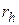есть ранг матрицы .

1.9 Подобные матрицы

Матрицы 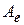и 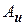линейного оператора связаны между собой с помощью матрицы перехода от одного базиса к другому

.

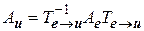Эта формула приводит к следующему определению. Пусть , 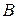– квадратные матрицы одного и того же порядка с элементами из поля 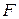. Будем матрицы и 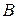называть подобными над полем 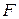, если существует обратимая матрица (то есть невырожденная: 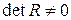) того же порядка с элементами из поля 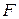такая, что

.

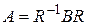Матрицу или ее обратную будем называть матрицей, осуществляющей подобие.

То, что матрицы и 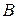подобны, будем записывать так: 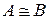. Отметим, что отношение подобия является отношением эквивалентности на множестве всех квадратных матриц одного и того же порядка, так как выполняются следующие свойства:

1. Отношение подобия рефлексивно: ;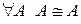

2. Отношение подобия симметрично: если 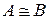, то ;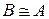

3. Отношение подобия транзитивно: если 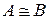и , то .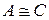

Значит множество всех квадратных матриц одного и того же порядка разбивается на непересекающиеся классы подобных между собой матриц. Матрицы 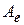и 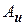одного оператора подобны и, следовательно, принадлежат одному классу. В каждом таком классе нет других матриц, кроме матриц одного и того же оператора. Точнее, пусть 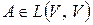, , 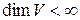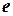– базис в пространстве и матрица 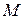подобна матрице 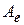. Тогда существует такой базис в пространстве , что .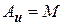

Если 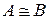, то 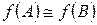для любого многочлена 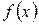. В частности, 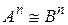для всех .

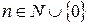Характеристические многочлены подобных матриц равны. Обратное утверждение неверно, то есть существуют неподобные матрицы, у которых равны их характеристические многочлены.

Имеет место следующий критерий подобия матриц.

Теорема 1.16 Пусть характеристические многочлены матриц и 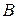с элементами из поля 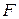раскладываются на линейные множители над полем 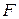. Тогда для того, чтобы эти матрицы были подобными над полем 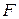необходимо и достаточно, чтобы их жордановы нормальные формы совпадали с точностью до порядка следования жордановых клеток.

Если 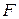есть поле комплексных чисел, то любой многочлен степени 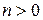можно разложить на линейные множители. Тогда для того, чтобы две комплексные матрицы были подобны необходимо и достаточно, чтобы их жордановы нормальные формы совпадали с точностью до порядка следования жордановых клеток. Из этого критерия следует, что для проверки подобия комплексных матриц нужно найти и сравнить их жордановы нормальные формы. 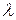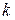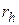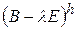Последние совпадут с точностью до порядка следования клеток тогда и только тогда, когда совпадут их характеристические многочлены, и для каждого собственного значения , имеющего алгебраическую кратность , равны ранги матриц и для всех .

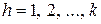2 ЕВКЛИДОВЫ ПРОСТРАНСТВА

2.1 Вещественное евклидово пространство и его простейшие свойства

Вещественное линейное пространство 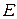называется вещественным евклидовым пространством (или просто евклидовым пространством), если выполнены следующие два требования:

І. Имеется правило, посредством которого любым двум элементам этого пространства и ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое символом .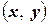

ІІ. Указанное правило подчинено следующим четырем аксиомам:

1°. 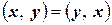(переместительное свойство или симметрия).

2°. (распределительное свойство).

3°. для любого вещественного .

4°. , если – ненулевой элемент; , если – нулевой элемент.

Приведем примеры евклидовых пространств.

Пример 1 Рассмотрим линейное пространство 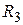всех свободных векторов. Скалярное произведение любых двух векторов определим так, как это было сделано в аналитической геометрии (т.е. как произведение длин этих векторов на косинус угла между ними). В курсе аналитической геометрии была доказана справедливость для так определенного скалярного произведения аксиом 1° – 4°). Стало быть, пространство 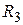с так определенным скалярным произведением является евклидовым пространством.

Пример 2 Рассмотрим бесконечномерное линейное пространство 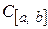всех функций , определенных и непрерывных на сегменте 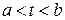. Скалярное произведение двух таких функций и 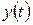определим как интеграл (в пределах от 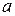до ) от произведения этих функций

.

Элементарно проверяется справедливость для так определенного скалярного произведения аксиом 1° – 4°. В самом деле, справедливость аксиомы 1° очевидна; справедливость аксиом 2° и 3° вытекает из линейных свойств определенного интеграла; справедливость аксиомы 4° вытекает из того, что интеграл от непрерывной неотрицательной функции 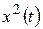неотрицателен и обращается в нуль лишь тогда, когда эта функция тождественно равна нулю на сегменте 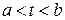(т.е. является нулевым элементом рассматриваемого пространства). Таким образом, пространство 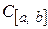с так определенным скалярным произведением представляет собой бесконечномерное евклидово пространство.

Пример 3 Следующий пример евклидова пространства дает 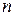-мерное линейное пространство упорядоченных совокупностей 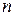вещественных чисел, скалярное произведение двух любых элементов 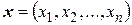и 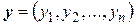которого определяется равенством

.

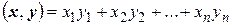Справедливость для так определенного скалярного произведения аксиомы 1° очевидна; справедливость аксиом 2° и 3° легко проверяется (достаточно вспомнить определение операций сложения элементов и умножения их на числа; наконец, справедливость аксиомы 4° вытекает из того, что 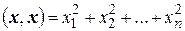всегда является неотрицательным числом и обращается в нуль лишь при условии .

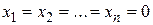Рассмотренное в этом примере евклидово пространство часто обозначают символом .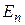

Пример 4 В пространстве 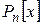всех многочленов степени не выше 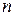с вещественными коэффициентами можно определить скалярное произведение таким образом

для любых многочленов

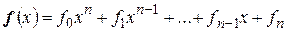и .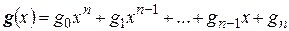

Устанавливаемые ниже свойства справедливы для произвольного евклидова пространства как конечной, так и бесконечной размерности.

Теорема 2.1 Для любых двух элементов и произвольного евклидова пространства справедливо неравенство

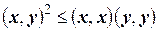, (2.1)

называемое неравенством Коши-Буняковского.

Линейное пространство называется нормированным, если выполнены следующие два требования:

І. Имеется правило, посредством которого каждому элементу пространства R ставится в соответствие вещественное число, называемое нормой (или длиной) указанного элемента и обозначаемое символом .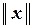

ІІ. Указанное правило подчинено следующим трем аксиомам:

1°. , если – ненулевой элемент, , если – нулевой элемент.

Date: 2015-08-24; view: 2292; Нарушение авторских прав