
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Нүкте қозғалысының берілу тәсілдері
ПӘННІҢ ОҚУ-ӘДІСТЕМЕЛІК КЕШЕНІ
| Теориялық механика (Кинематика) | ||
| (оқу жұмыс жоспарына сәйкес пәннің коды мен | ||
| пәні бойынша | ||
| толық атауы) | ||
| 5B073200 – Стандартизация, метрология және сертификация | мамандығының студенттеріне | |
| (мамандық атауы және шифрі) | ||
| арналған | ||
Астана
Дәріс-1. Кинематикаға кіріспе. Нүкте кинематикасы.
Кинематикаға кіріспе
Кинеметика деп – материялық денелер қозғалысының геометриялық сипаттамаларын (траекториясын, жылдамдығын, үдеуін), зерттейтін теориялық механика тарауын айтады. Кинематикада денелердің қозғалысы оған әсер ететін күштерге тәуелсіз, тек геометриялық тұрғыдан зерттеледі. Дененің қозғалысы деп оның басқа бір қозғалмайтын денеге қатысты орын ауыстыруын айтады. Осы қозғалмайтын денемен байланысқан координата жүйесін санақ жүйесі деп атайды.
Теориялық механикада уақыт үздіксіз өзгеріп отыратын шама болып есептеледі. Ол дене қозғалысына тәуелсіз, кез келген санақ жүйесінде және кеңістіктің кез келген нүктесінде бірдей, қайталанбайтын, оң таңбалы скаляр шама.
Жалпы жағдайда қозғалатын дененің нүктелері әртүрлі қозғалыс жасайды. Сондықтан алдымен нүкте қозғалысын қарастырамыз.
Нүкте кинемтикасы
Жүріп өткен жолымен салыстырғанда өлшемі әлдеқайда кіші денені кинематикада нүкте деп атайды. Нүкте қозғалысының негізгі кинематикалық сипаттамаларына оның траекториясы, жылдамдығы және үдеуі жатады. Нүкте кинематикасында мынадай екі негізгі мәселе қарастырылады:
1) Нүкте қозғалысының берілу тәсілдерін анықтау;
2) Берілу тәсілдеріне қарай нүктенің барлық кинемтикалық сипаттамаларын (траекториясын, жылдамдығы мен үдеуін) анықтау.
Нүкте қозғалысының берілу тәсілдері
Нүкте қозғалысын беру деп кез келген уақытта нүктенің кеңістіктегі орнын табуға мүмкіндік беретін тәсілді алуды айтады. Кинематикада нүкте қозғалысы үш түрде: векторлық, координаталық және табиғи тәсілдермен беріледі.
1. Векторлық тәсіл. Бұл тәсілде нүктенің  радиус-векторы уақытқа тәуелді функция ретінде беріледі, яғни
радиус-векторы уақытқа тәуелді функция ретінде беріледі, яғни
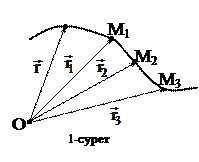
 (1)
(1)
Нүктенің радиус-векторы координата жүйесінің бас нүктесі болатын бір О нүктесінен жүргізіледі, бірақ координата жүйесінің берілуі нақтыланбайды (1-сурет). (1) теңдеу нүктенің қозғалыс заңы деп аталады.
Уақыт өзгерген кездегі радиус-вектор ұшының кеңістіктегі геометриялық орындары нүктенің траекториясы немесе радиус-вектордың годографы деп аталады. Егер нүктенің траекториясы түзу болса оның қозғалысы түзу сызықты қозғалыс, ал қисық болса – қисық сызықты қозғалыс деп аталады.
2.  Координаталық тәсіл. Бұл тәсіл міндетті түрдекоордината жүйесінің берілуін талап етеді.
Координаталық тәсіл. Бұл тәсіл міндетті түрдекоордината жүйесінің берілуін талап етеді.  жүйесіндегі кез келген М нүктенің орны оның
жүйесіндегі кез келген М нүктенің орны оның  координаталарымен анықталады. Нүкте қозғалған кезде оның
координаталарымен анықталады. Нүкте қозғалған кезде оның 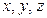 координаталары өзгереді де уақытқа тәуелді функциялар болады (2-сурет):
координаталары өзгереді де уақытқа тәуелді функциялар болады (2-сурет):
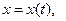
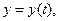
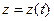 . (2)
. (2)
Бұл теңдеулер нүктенің декарттық координата жүйесіндегі қозғалыс теңдеулері деп аталады.
Нүктенің траекториясының теңдеуін координаталық түрде жазу үшін (2) теңдеулерінен уақытты жою қажет.
2-суреттен векторлық және координаталық тәсілдердің арасындағы байланысты аламыз:
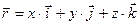 . (3)
. (3)
Егер қозғалыс сфералық немесе цилиндрлік координата жүйесінде қарастырылса, онда нүктенің сәйкес координаталары уақыт функциялары ретінде беріледі:
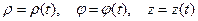 , (4)
, (4)
 . (5)
. (5)
(4) теңдеулері нүктенің цилиндрлік координата жүйесіндегі, ал (5) теңдеулері – сфералық координата жүйесіндегі қозғалыс теңдеулері болады.
Нүкте бір жазықтықта қозғалған жағдайда оның қозғалысы полярлық координата жүйесінде берілуі мүмкін:
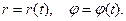 (6)
(6)
Бір жағынан цилиндрлік, сфералық, полярлық координата жүйелерінің арасында, ал екінші жағынан декарттық координата жүйесінің арасында белгілі байланыстар бар:
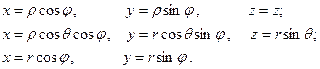
3. Табиғи тәсіл. Табиғи тәсілде нүкте траекториясы алдын ала белгілі болған жағдайда пайдаланады. Бұл тәсілде нүктенің траекториясы, траектория бойындағы доғаның бастапқы орны, қозғалыстың оң бағыты мен 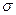 доғалық координатасы уақытқа тәуелді функция ретінде беріледі (3-сурет), демек:
доғалық координатасы уақытқа тәуелді функция ретінде беріледі (3-сурет), демек:

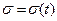 . (7)
. (7)
Бұл – қозғалысы табиғи тәсілмен берілген нүкте қозғалысының заңы (теңдеуі).
Сонымен, нүктенің қозғалысын табиғи тәсілмен анықтау үшін оның траекториясы, бас нүктесі, траектория бойымен қозғалыс заңы (7) берілуі қажет екен.
Егер нүкте оң бағытта қозғалса доға дифференциалы  , ал теріс бағытта қозғалса бұл дифференциал нөлден кіші болатынын айту керек.
, ал теріс бағытта қозғалса бұл дифференциал нөлден кіші болатынын айту керек.
Нүктенің жүріп өткен жолы әрқашан оң болады, яғни 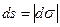 .
.
Табиғи және координаталық әдістердің арасында мынадай байланыс бар:
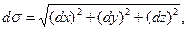
мұндағы 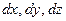 – нүкте координаталарының дифференциалдары.
– нүкте координаталарының дифференциалдары.
Date: 2015-09-03; view: 5222; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |