Основные теоретические сведения. 1. Если в некоторой окрестности точки выполняется неравенство или , то точка называется точкой экстремума функции (соответственно точкой максимума или

1. Если в некоторой окрестности точки 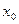выполняется неравенство 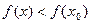или , то точка 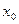называется точкой экстремума функции 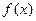(соответственно точкой максимума или минимума). Необходимое условие экстремума: если 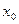- экстремальная точка функции 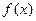, то первая производная 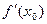либо равна нулю или бесконечности, либо не существует. Достаточное условие экстремума: 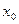является экстремальной точкой функции 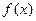, если ее первая производная 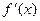меняет знак при переходе через точку 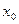: с плюса на минус – при максимуме, с минуса на плюс - при минимуме.

2. Точка 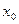называется точкой перегиба кривой 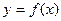, если при переходе через точку 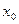меняется направление выпуклости. Необходимое условие точки перегиба: если 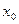- точка перегиба кривой 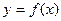, то вторая производная 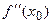либо равна нулю или бесконечности, либо не существует. Достаточное условие точки перегиба: 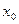является точкой перегиба кривой 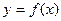, если при переходе через точку 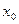вторая производная 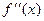меняет знак.

3. Прямая 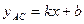называется наклонной асимптотой кривой 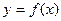, если расстояние от точки 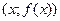кривой до этой прямой

стремится к нулю при .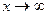
При этом

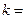
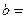
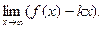(1)

При 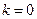имеем горизонтальную асимптоту: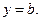

Если

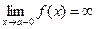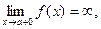или (2)

то прямая 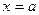называется вертикальной асимптотой.

4. Общая схема исследования функции и построения ее графика.

Изучение заданной функции и построение ее графика целесообразно проводить по следующей схеме:

1⁰. Найти область определения и точки разрыва; вычислить значения функции (или соответствующих пределов) в граничных точках области определения.

2⁰. Исследовать вопрос о четности или нечетности, периодичности функции.

3⁰. Определить нули функции и интервалы ее знакопостоянства.

4⁰. Найти асимптоты.

5⁰. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями.

6⁰. Исследовать функцию на экстремум, определить интервалы ее монотонности.

7⁰. Найти точки перегиба и интервалы выпуклости и вогнутости графика функции.

8⁰. Построить график, учитывая исследование, проведенное в п.п.1⁰-7⁰.

Отметим, что эта далеко не полная схема позволяет тем не менее успешно строить графики подавляющего большинства функций, встречающихся на практике.

5. Неопределенным интегралом от функции f(x) называется выражение вида 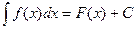, если 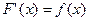. Функция F(x) называется первообразной для заданной функции f(x).

При интегрировании наиболее часто используются ниже перечисленные методы.

1) Если 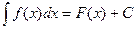, то

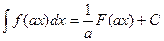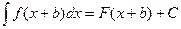; , (3)

где a и b – некоторые постоянные.

2) Подведение под знак дифференциала:

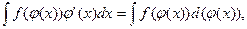(4)

так как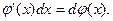

3) Формула интегрирования по частям:

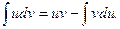(5)

Обычно выражение dv выбирается так, чтобы его интегрирование не вызывало особых затруднений. За u, как правило, принимается такая функция, дифференцирование которой приводит к ее упрощению. К классам функций, интегрируемых по частям, относятся, в частности, функции вида ,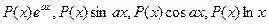

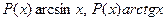, где P(x) – многочлен от x.

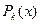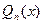4) Интегрирование рациональных дробей, т.е. отношений двух многочленов и (соответственно k -й и n -й степени): 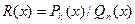, сводится к разложению подынтегральной функции R(x) на элементарные, всегда интегрируемые дроби вида

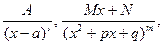(6)

где l и m – целые положительные числа, а трехчлен x²+px+q не имеет действительных корней. При этом в случае неправильной дроби (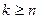) должна быть предварительно выделена целая часть.

5) Интегрирование методом замены переменной (способом подстановки) является одним из эффективных приемов интегрирования. Его сущность состоит в переходе от переменной x к переменной 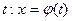. Наиболее целесообразная для данного интеграла замена переменной, т.е. выбор функции j(t), не всегда очевидна. Однако для некоторых часто встречающихся классов функций можно указать такие стандартные постановки:

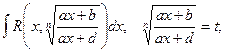
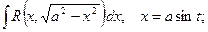
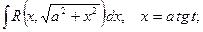
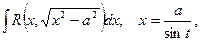
где R – символ рациональной функции.

6. Формула Ньютона – Лейбница для вычисления определенного интеграла имеет вид

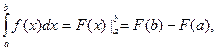(7)

если 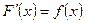и первообразная F(x) непрерывна на отрезке .

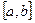Определенный интеграл численно равен площади криволинейной трапеции, ограниченной прямыми x=a, x=b, y=0 и частью графика функции y=f(x), взятой со знаком плюс, если f(x) 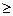0, и со знаком минус, если f(x) 0.

7. Если интервал интегрирования 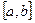не ограничен (например, ) или функция f(x) не ограничена в окрестности одного из пределов интегрирования (например, при 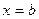), то по определению полагают

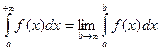, (8)

и

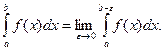(9)

Интегралы в левых частях равенств (8) и (9) называются несобственными интегралами. Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенств (8) и (9). Если же предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся.

8. Пусть криволинейная трапеция, ограниченная прямыми 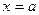, , 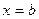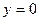и частью графика кривой 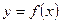, вращается вокруг оси Оx. Тогда объем полученного при этом тела вращения вычисляется по формуле

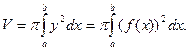(10)

Пример 1. Исследовать на экстремум функцию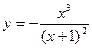

Решение: Находим первую производную: 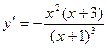. Из уравнени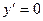й и 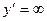получаем точки, «подозрительные» на экстремум: 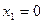, , 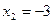. Исследуем их, определяя знак первой

производной слева и справа от каждой точки. Для наглядности результаты представим в виде таблицы изменения знака :

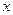
	(- ,-3)	-3	(-3,-1)	-1	(-1,0)		(0,+ )
	-		+		-		-
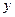
	убыв.	min	возр.	не опр.	убыв.		убыв.

В первой строке указаны интервалы, на которые область определения функции разбивается точками 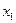, , , 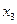и сами эти точки. Во второй строке указаны знаки производной в интервалах монотонности. В третьей строке приведено заключение о поведении функции.

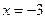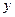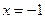Исследуемая функция, как следует из таблицы, имеет минимум в точке : (-3) . Точки и 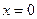не являются точками экстремума, так как в первой точке функция не определена, а в окрестности второй точки первая производная сохраняет знак.

Пример 2. Найти асимптоты графика функции .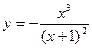

Решение: Точка 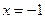является точкой разрыва функции. Так как 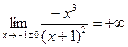, то прямая 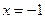служит вертикальной асимптотой графика функции [см. формулы (2)].

Ищем наклонные асимптоты 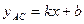, используя формулы (1):

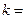
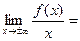
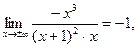
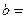
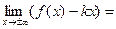
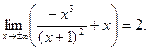
Таким образом, уравнение наклонной асимптоты имеет вид .

Пример 3. Построить график функции 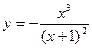, используя общую схему исследования функции.

Решение: 1⁰. Область определения – вся числовая ось, кроме точки 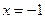, в которой функция терпит разрыв. Находим предельные значения функции:

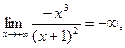
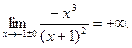
2⁰. Функция общего вида, непериодическая.

3⁰. Функция имеет один нуль в точке 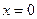. Функция положительна при 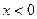и отрицательна при .

4⁰. График функции имеет одну вертикальную асимптоту 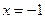и одну наклонную асимптоту 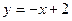(см. пример 2).

5⁰. График функции пересекает координатные оси в точке (0;0).

6⁰. Функция имеет один минимум при 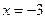. На интервалах (- ; -3)È(-1; 0)È(0; + ) функция монотонно убывает, на интервале (-3; -1) – монотонно возрастает (см. пример 1).

7⁰. Вторая производная 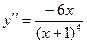обращается в бесконечность при 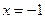и равна нулю в точке 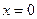, которая является единственной точкой перегиба (см. таблицу):

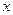
	(- , -1)	-1	(-1, 0)		(0, + )
	+		+		-
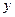
	È	не опр.	È	точка перегиба	Ç

На интервалах (- ; -1)È(-1; 0) функция выпукла вниз (вогнута), на интервале (0; + ) – выпукла вверх. Ордината точки перегиба .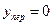

8⁰. Учитывая полученные результаты, строим график функции 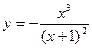(рис.10).

Рис.10

Пример 4. Найти .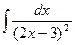

Решение. Так как 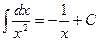, то, используя формулы (3), получим

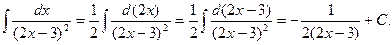
Проверка:

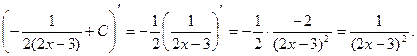
Пример 5. Найти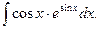

Решение. Так как 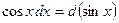, то по формуле (4) находим

Пример 6. Найти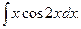

Решение. Применим метод интегрирования по частям. Положим 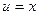, , 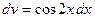тогда 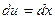, 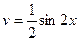. Используя формулу (5), имеем

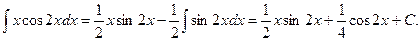
Пример 7. Найти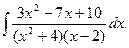

Решение. Подынтегральная рациональная дробь является правильной и разлагается на элементарные дроби вида (6):

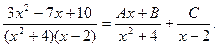
Освобождаясь от знаменателей в обеих частях этого равенства и приравнивая числители, получаем тождество для вычисления неопределенных коэффициентов А, В и С:

Составим систему трех уравнений с тремя неизвестными. Одно уравнение получим, полагая x=2 (корень знаменателя подынтегральной функции). Два других получим, приравнивая коэффициенты при одинаковых степенях х в обеих частях тождества, например при х² и х⁰:

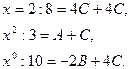
Решение этой системы дает: А=2, В=-3, С=1. Таким образом,

.

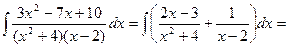
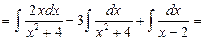
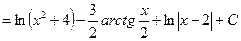Пример 8. Вычислить определенный интеграл .

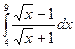Решение. Применим метод замены переменной; положим 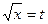, откуда 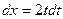. Найдем пределы интегрирования по переменной t: при x= 4 имеем t= 2, а при x= 9 имеем t= 3. Переходя в исходном интеграле к новой переменной t и применяя формулу Ньютона – Лейбница (7), получаем

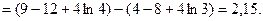
Пример 9. Вычислить несобственный интеграл или установить его расходимость: 1)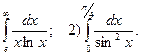

Решение. 1) Первый интеграл является несобственным интегралом с бесконечным верхним пределом интегрирования. Согласно определению (8), имеем

Следовательно, данный интеграл расходится.

2) Второй интеграл является несобственным интегралом от неограниченной функции; 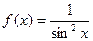терпит бесконечный разрыв в нижнем пределе при x= 0. Согласно определению (9), получаем

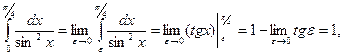
т.е. этот несобственный интеграл сходится.

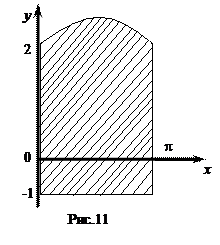
Пример 10. Вычислить площадь плоской фигуры, ограниченной кривыми 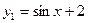, , 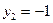, 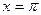(рис.11).

Решение.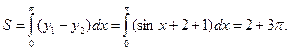

Пример 11. Вычислить объем тела, образованного вращением вокруг оси О х кривой

Решение. Объем полученного тела вращения найдем по формуле (10):

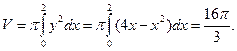
Date: 2015-08-15; view: 552; Нарушение авторских прав