
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Алгоритм метода потенциалов
1. Если не сказано иное, 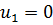 (потенциал первой строки).
(потенциал первой строки).
Находим значения потенциалов u и v по заполненным клеткам (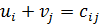 ).
).
2. Определяем оценки свободных переменных (свободных клеток).
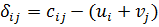
Оценки показывают, насколько изменится целевая функция, если эту клетку сделать заполненной с грузом, равным 1.
21. Признак неоптимальности базисного решения транспортной задачи. Определение цикла. Построение улучшенного решения.
Если при проверке решения на оптимальность методом потенциалов какая-то оценка свободной переменной получилась отрицательной, то решение не является оптимальным, и его можно улучшить, построив цикл распределения.
Для того, чтобы построить улучшенное базисное решение:
1. Находят свободную клетку с отрицательной оценкой (как правило, наибольшая по модулю отрицательная, т.е. самая отрицательная).
Выбранную клетку будем называть «зап» клетка – заполняемая клетка.
2. Строят цикл.
Цикл – замкнутая ломаная линия, которая начинается и заканчивается в «зап» клетке. Звенья параллельны строкам и столбцам таблицы. Вершины – в занятых клетках и в «зап» клетке, все углы прямые.
Звенья цикла могут проходить сквозь занятые клетки, цикл может иметь точки самопересечения в пустых клетках.
Справедлива теорема, что для любого опорного плана и любой свободной клетки всегда можно построить цикл, причем единственным образом (для данной клетки).
3. Выбирают «ос» клетку – освобождаемую клетку.
В вершинах цикла проставляются в чередующемся порядке знаки +/-, начиная со знака + в «зап» клетке.
Не имеет значения направление обхода цикла – по часовой стрелке или против.
В качестве «ос» клетки выбирается клетка с минусом, с наименьшим грузом.
4. Строят новый опорный план.
Груз из «ос» клетки записывается в «зап» клетку и прибавляется во все клетки цикла с плюсом, вычитается из всех клеток цикла с минусом. «Ос» клетка становится пустой.
Таким образом, в новой таблице переменная, соответствующая «зап» клетке стала базисной, а соответствующая «ос» клетке – свободной.
Изменение целевой функции – произведение оценки «зап» клетки на груз из «ос» клетки: 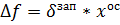
Замечения:
1. Если имеется несколько претендентов на «зап» клетку, то лучше выбрать ту, где стоимость перевозки меньше.
2. Если несколько претендентов на «ос» клетку, то лучше выбрать ту, где стоимость перевозки наибольшая. В оставшуюся клетку с минусом с таким же грузом поставить 0 (вырожденное решение).
3. Если в оптимальном решении есть свободная клетка с нулевой оценкой, то это признак наличия альтернативного решения. Чтобы его найти, нужно эту клетку выбрать в качестве «зап» клетки.
22. Неуравновешенная транспортная задача: постановка и решение. Фиктивные пункты отправления и назначения.
Задача называется неуравновешенной, если не выполняется условие равновесия (баланса). То есть количество груза во всех ПО не равно требуемому грузу во всех ПН.
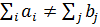 .
.
1. Если 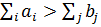 , т.е. если в ПО груза больше, чем требуется, то нужно ввести фиктивный ПН. В него поместить лишний груз:
, т.е. если в ПО груза больше, чем требуется, то нужно ввести фиктивный ПН. В него поместить лишний груз: 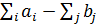 .
.
Стоимость перевозки в фиктивный ПН=0 (т.к. этого пункта реально не существует).
2. Если  , т.е. если имеется меньше, чем требуется, то вводится фиктивный ПО, из которого вывозится недостающий груз, (
, т.е. если имеется меньше, чем требуется, то вводится фиктивный ПО, из которого вывозится недостающий груз, (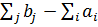 ).
).
Стоимость перевозки из фиктивного ПО=0 (этого ПО реально не существует, везти в ПН нечего).
При составлении опорного плана сначала распределяем реальные ПО и ПН, а в фиктивные записываем, что останется.
23. Неуравновешенная транспортная задача с дополнительным условием.
Дополнительное условие может быть двух видов:
1. Условие, что какой-то ПО вывезен полностью (если 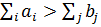 ).
).
Нужно запретить маршрут из этого ПО в фиктивный ПН, для этого нужно поставить высокую стоимость перевозки - М (в этот пункт будет невыгодно везти). Стоимость перевозки в остальные фиктивные пункты равна 0.
2. Условие, что какой-то ПН удовлетворен полностью (если 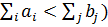 .
.
Аналогично ставим большую стоимость перевозки в этот пункт – М. В остальные фиктивные пункты стоимость перевозки=0.
Заполняем как обычно, но клетку со стоимостью М оставляем пустой. При проверке решения на оптимальность оценка этой клетки будет всегда положительной (М минус сумма потенциалов всегда число положительное, т.к. М – очень велико).
Можно начать заполнять именно с этого доп. условия. То есть сначала по методу наименьшей стоимости заполняем строку или столбец, о котором говорится в доп. условии, потом по методу наименьшей стоимости всю остальную таблицу.
24. Способ задания бескоалиционной игры. Основные понятия (множества игроков, стратегий, ситуаций; функция выигрыша; сумма игры).
В бескоалиционной игре каждый участник преследует только свои интересы.
Число участников игры – I
Множество стратегий игрока – Ti (то, как себя может вести игрок)
Множество ситуаций – S (элементы множества ситуаций являются n-мерным вектором) Ситуации – то, что может произойти во время игры.
Функция выигрыша игрока в конкретной ситуации – Hi(Sj) (что получит игрок, если произойдет то-то и то-то).
Для того, чтобы решить игру, строят платежную матрицу, слева пишут стратегии одного игрока, сверху – другого. в матрице, на пересечении их стратегий записывается возможный выигрыш (или проигрыш), который получит первый игрок, если выберет свою стратегию, соответствующую данной строчке, а его противник – свою стратегию, соответствующую данному столбцу.
Игра с постоянной суммой – 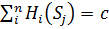 – суммы по всем строкам и столбцам равны.
– суммы по всем строкам и столбцам равны.
Чтобы задать игру нужно задать множество участников, множество стратегий, выигрыш каждого участника в каждой ситуации.
Игра Г называется эквивалентной игре Г’, если он различаются выигрышем каждого игрока:
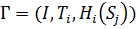
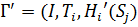
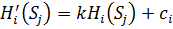
Свойства эквивалентных игр:
1. Рефлексивность: игра эквивалентна самой себе
2. Симметрия: если игра Г эквивалентна игре Г’, то и Г’ эквивалентна Г/
3. Транзитивность: если Г эквивалентна Г’, а Г’ эквивалентна Г’’, то Г эквивалентна Г’’.
25. Антагонистическая (матричная) игра. Ситуация равновесия. Ситуация равновесия в чистых стратегиях.
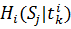 – выигрыш i игрока, когда он применял свою k-стратегию.
– выигрыш i игрока, когда он применял свою k-стратегию.
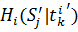 – выигрыш i игрока, когда он свою стратегию поменял, а остальные игроки свою стратегию сохранили (игрок поменял свою стратегию в одностороннем порядке).
– выигрыш i игрока, когда он свою стратегию поменял, а остальные игроки свою стратегию сохранили (игрок поменял свою стратегию в одностороннем порядке).
Ситуация называется приемлемой для игрока, если ему невыгодно в одностороннем порядке менять свою стратегию.
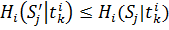
Может быть ситуация, приемлемая для всех игроков сразу – если никому из игроков не выгодно менять свою стратегию в одностороннем порядке.
Ситуация, приемлемая для всех игроков – ситуация равновесия.
Стратегии, входящие в ситуацию равновесия – равновесные стратегии.
Антагонистическая игра – игра двух лиц с нулевой суммой.
Для антагонистической игры можно ввести платежную матрицу.
Элементы платежной матрицы - 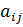 – выигрыш игрока А в ситуации, когда он выбрал стратегию I, а игрок В – стратегию j.
– выигрыш игрока А в ситуации, когда он выбрал стратегию I, а игрок В – стратегию j.
Если платежная матрица имеет седловую точку, то говорят, что она имеет ситуацию равновесия в чистых стратегиях.
Седловая точка – см. билет 26.
Если матрица имеет седловую точку, то соответствующие стратегии являются равновесными для обоих игроков, соответствующий элемент матричной таблицы – цена игры – равен выигрышу первого в состоянии равновесия и проигрышу второго.
У первого игрока m чистых стратегий. Каждой чистой стратегии соответствуют элементы строки.
У второго игрока n чистых стратегий. Каждой стратегии соответствуют элементы столбца.
Чтобы определить ситуацию равновесия, нужно найти maxmin и minmax. Если они совпадают, то существует равновесная ситуация в чистых стратегиях. Выигрыш равен соответствующему элементу матрицы и равен цене игры.

Оптимальные стратегии – чистые стратегии.
Все равновесные стратегии являются осторожными.
Maxmin – выигрыш, который может гарантировать себе первый игрок независимо от того, что делает второй.
Minmax – то, что может заплатить второй игрок (его проигрыш) при любых действиях первого.
В соответствии с этим maxmin называют нижней ценой игры, а minmax – верхней ценой игры.
26. Понятие о максимине и минимаксе. Необходимое и достаточное условие существования равновесия в чистых стратегиях. Цена игры.
Максимин как и следует из названия, является максимумом, взятым от минимума функции. Соответственно минимакс – минимум, взятый от максимума функции.
Пусть дана функция двух переменных, для которой существует максимум по х и минимум по у. Тогда между максимином и минимаксом существует соотношение: максимин не превосходит минимакс.

Доказательство:
Пусть дана функция 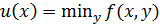 и функция
и функция 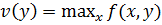 .
.
Так как минимум функции никогда не превосходит максимум (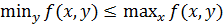 ). То есть, для любых х и у выполняется неравенство:
). То есть, для любых х и у выполняется неравенство: 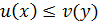 .
.
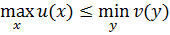
Точка является седловой точкой функции двух переменных, если имеет место двойное неравенство: 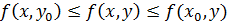 . То есть значение функции может лишь уменьшится при фиксированном х и может только увеличиться при фиксированном у.
. То есть значение функции может лишь уменьшится при фиксированном х и может только увеличиться при фиксированном у.
Для того, чтобы точка была седловой точкой функции, для которой существуют максимум по х и минимум по у, необходимо и достаточно, чтобы максимин этой функции равнялся минимаксу и равнялся значению функции в этой точке.
Матричная форма записи: для того, чтобы пара (i0,j0) являлась седловой точкой для элементов матрицы, необходимо и достаточно, чтобы максимин равнялся минимаксу и равнялся соответствующему элементу матрицы (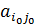 ).
).
Так как ситуация равновесия – это существование седловой точки для данной игры, поэтому необходимое и достаточное условие существования равновесия в чистых стратегиях звучит похоже на ранее сформулированное:
Для того, чтобы для игры существовала ситуация равновесия, необходимо и достаточно, чтобы максимин равнялся минимаксу и равнялся цене игры.
Цена игры – выигрыш первого и проигрыш второго в седловой точке.
27. Определение смешанной стратегии. Математическое ожидание выигрыша первого игрока в случае смешанных стратегий. Определение точки равновесия в смешанных стратегиях.
Каждую из своих стратегий игроки будут выбирать с некоторой вероятностью: нужно определить вероятность выбора каждой стратегии.
pi – вероятность выбора стратегии i первым игроком.
qj – вероятность выбора стратегии j вторым игроком.
Смешанной стратегией называется случайная величина, значения которой – чистые стратегии.
Выигрыш – тоже случайная величина (чтобы выиграть 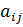 нужно, чтобы первый выбрал стратегию i, и второй выбрал стратегию j, т.е. вероятность выигрыша равна произведению вероятностей:
нужно, чтобы первый выбрал стратегию i, и второй выбрал стратегию j, т.е. вероятность выигрыша равна произведению вероятностей: 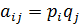 ).
).
Матожидание выигрыша первого игрока 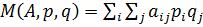 . Произведение каждого элемента на каждую вероятность выбора той или иной стратегии.
. Произведение каждого элемента на каждую вероятность выбора той или иной стратегии.
Также может быть записано как 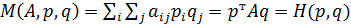 .
.
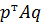 – средний выигрыш первого игрока, если дана платежная матрица и векторы вероятностей.
– средний выигрыш первого игрока, если дана платежная матрица и векторы вероятностей.
Ситуация (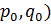 является ситуацией равновесия в смешанных стратегиях, если выполняется двойное неравенство:
является ситуацией равновесия в смешанных стратегиях, если выполняется двойное неравенство: 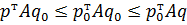 . Т.е. если первый сойдет со своей стратегии, то ему будет только хуже, если второй сойдет со своей стратегии, то он проиграет больше.
. Т.е. если первый сойдет со своей стратегии, то ему будет только хуже, если второй сойдет со своей стратегии, то он проиграет больше.
Для того, чтобы 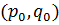 являлась ситуацией равновесия, необходимо и достаточно, чтобы максимин равнялся минимаксу, равнялся цене игры.
являлась ситуацией равновесия, необходимо и достаточно, чтобы максимин равнялся минимаксу, равнялся цене игры.
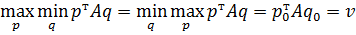
Решить игру в смешанных стратегиях значит найти 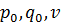 .
.
28. Теорема о существовании точки равновесия в случае смешанных стратегий. Теорема о цене игры в случае применения одним из игроков чистых стратегий.
Какова бы не была матрица А в антагонистической игре, ситуация равновесия всегда существует, то есть выполняется определение равновесия и выполняется условие:
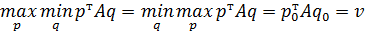
Цена игры может быть достигнута даже в том случае, когда один игрок применяет чистые стратегии, а другой – смешанные, причем экстремум достигается на оптимальной смешанной стратегии.
Обозначим 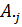 – столбец j.
– столбец j. 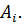 – строка i.
– строка i.
Если первый игрок применяет чистые стратегии (строчки), то 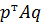 переходит в выражение:
переходит в выражение: 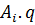 .
.
Если второй игрок применяет чистые стратегии (столбцы), то 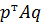 переходит в выражение
переходит в выражение 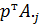 .
.
Т.е. имеет место равенство:
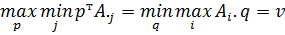
Внешний экстремум на смешанных стратегиях, внутренний – на чистых.
29. Связь цены игры с нижней ценой игры и верхней ценой игры.
Цена игры находится между максимином и минимаксом
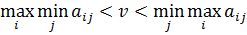
То есть, цена игры находится между нижней ценой игры и верхней ценой игры.
30. Графическое решение игры в случае наличия у одного из игроков двух чистых стратегий.
Если у одного из игроков имеется только две стратегии, то игру можно решить графическим методом (найти смешанные оптимальные стратегии и цену игры).
У кого две стратегии – тот экстремум внешний.
1) Определяем максимин и минимакс. Цена игры лежит между этими числами.
2) 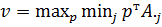 – перебираем все чистые стратегии второго по очереди, выбираем минимум из них.
– перебираем все чистые стратегии второго по очереди, выбираем минимум из них.
Две стратегии игрока раскладываем в виде 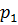 ,
, 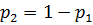 (т.к. вероятность равна единице – игрок все равно выберет какую-то из своих двух стратегий).
(т.к. вероятность равна единице – игрок все равно выберет какую-то из своих двух стратегий).
3) Определяем выигрыши первого игрока, когда он применяет свою смешенную, а второй свои чистые стратегии.
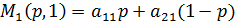
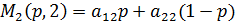
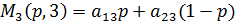
Строим эти прямые (одна точка при p=0, вторая – при p=1).
Если мы перебираем чистые стратегии второго игрока (столбцы), то на графике нужно строить нижнюю огибающую (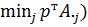 и искать на ней верхнюю точку (
и искать на ней верхнюю точку (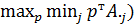 .
.
Если же две стратегии у второго игрока, то 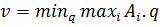 – т.е. перебираем все чистые стратегии первого игрока по очереди, выбираем максимум из них.
– т.е. перебираем все чистые стратегии первого игрока по очереди, выбираем максимум из них.
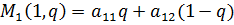
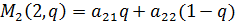
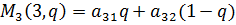
Аналогично строим прямые (одна точка при q=0, другая – при q=1). В этом случае нужна верхняя огибающая (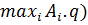 и нижняя точка на ней (
и нижняя точка на ней (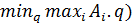 .
.
31. Доминирующие и доминируемые стратегии. Упрощение матрицы игры. Вероятности доминируемой стратегии в оптимальной смешанной.
Доминирующая стратегия – стратегия, которая приносит игроку больший выигрыш, чем другие.
Доминируемая стратегия – стратегия, которая не приносит лучшего результата, по сравнению с остальными.
Для того, чтобы 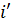 являлась доминирующей стратегией первого игрока по отношению к стратегии i, если имеет место равенство:
являлась доминирующей стратегией первого игрока по отношению к стратегии i, если имеет место равенство: 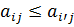 для всех j.
для всех j.
 является доминирующей стратегией второго игрока по отношению к j, если
является доминирующей стратегией второго игрока по отношению к j, если 
Вероятности доминируемых стратегий в оптимальной смешанной равны 0.
Поэтому можно упростить матрицу, вычеркнув «невыгодные» строки и столбцы.
Вычеркиваются «слишком тонкие» строки (каждый элемент такой строки меньше или равен элементу другой строки). Т.е. используя стратегию, соответствующую «слишком тонкой» строке, игрок выиграет меньше, чем мог бы.
Вычеркиваются «слишком толстые столбцы» (каждый элемент столбца больше или равен элементу другого столбца). Т.е., следуя данной стратегии, второй игрок проиграет больше, чем мог бы.
Упрощая платежную матрицу, мы приходим в состояние, когда у одного из игроков остается только две стратегии. Тогда возможно решить игру графическим способом.
32. Связь решения матричной игры с задачей линейного программирования для первого (второго) игрока.
Задачу антагонистической игры можно свести к двум взаимнодвойственным задачам линейного программирования
Пусть дана игровая матрица А’, для которой существуют элементы меньшие или равные нулю.
Нужно перейти к матрице А=А’+сS, где 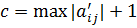 (
(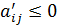 ).
).
Получаем новую матрицу, в которой все элементы уже положительны. Чтобы решить игру нужно найти 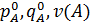 .
.
Для матрицы А нужно составить пару взаимнодвойственных задач:
| Прямая | Двойственная |
Y-?
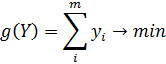
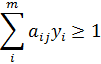
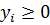
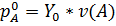 , если , если 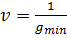
| X-?
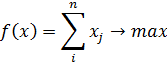
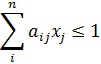
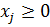
 , если , если 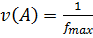
|
Оптимальный вектор для матрицы А равен оптимальному вектору для матрицы А’ (т.е. оптимальные стратегии 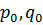 совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.
совпадают). Цена игры для матрицы А’ равна цене игры для матрицы А минус то число, которое мы прибавили вначале.
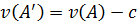 .
.
33. Понятие графа. Основные определения.
Задача сетевого планирования решается с помощью построения графа.
Граф – совокупность точек и связей между ними.
Точки называются вершинами (кружочки), а связи – дугами (стрелочки).
Если на каждой дуге указывается направление, то граф называется ориентированным.
Путь в графе – такая последовательность дуг, когда начало последующей дуги совпадает с концом предыдущей.
Начальная вершина – вершина, в которую не входит ни одна дуга.
Конечная вершина – вершина, из которой не выходит ни одна дуга.
34. Понятие о сетевом планировании. Построение сети, соответствующей данному проекту.
Сетевая модель представляет план выполнения некоторого комплекса работ.
Весь проект разбивается на несколько операций (работ).
Для построения сети, соответствующей данному проекту строят таблицу, в которой разбивают проект на отдельные работы и планируют время выполнения каждой:
| № работы | Работа, которая следует за данной | Время выполнения работы |
Некоторые работы могут выполняться одновременно друг с другом, а для некоторых работ требуется строгое соблюдение очередности (например, мы не можем построить крышу дома, пока н возвели фундамент и стены). Для этого и составляется второй столбик таблицы.
После заполнения таблицы нужно определить начальные работы. Это те работы, которые не следуют за другими.
Сначала рисуем кружок (начальную вершину). Из нее выходят дуги, соответствующие начальным работам. Каждая дуга приводит в последующую вершину (событие – результат выполненной работы). Далее в соответствии с таблицей строятся следующие дуги-работы, которые приводят в следующие вершины. Так продолжается, пока мы не придем в конечную вершину (конечный результат проекта, все работы завершены).
На каждой дуге проставляется запланированная продолжительность соответствующей работы.
35. Сетевой проект. Резервы времени событий (вершин) и работ (ребер). Критическое время выполнения проекта. Критический путь.
Для выполнения проекта нам необходимо знать, сколько времени отнимет его реализация, можем ли мы как-то сэкономить время или наоборот, есть ли у нас возможность сделать перерыв после выполнения отдельных работ.
Для этого нужно определить критический путь. Критический путь – это критическое время выполнения всех работ. То есть, это минимально возможное время, за которое можно выполнить весь проект.
Для его определения на уже построенном графе каждую вершину (каждый кружок) делим на 4 части. В верхней части проставляем номер вершины. Слева указывается раннее время наступления 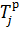 , справа – позднее время наступления
, справа – позднее время наступления 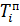 . В нижней части – резерв времени.
. В нижней части – резерв времени.
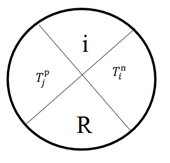
Раннее время наступления – самый ранний момент времени, к которому могут быть завершены все работы, входящие в данную вершину.
Позднее время наступления – самый поздний момент времени, к которому можно начать все работы, выходящие из этой вершины, чтобы можно было успеть выполнить весь проект за критическое время.
Резерв времени – разность между поздним и ранним временем. Показывает, какой перерыв мы можем сделать, прежде чем приступить к следующей работе и при этом успеть выполнить все в срок.
1. Сначала проставляется раннее время. В первом кружке ставится 0, в остальных определяется как максимум раннего времени предыдущего события и времени выполнения входящих в данную вершину работ.
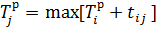
То есть, на дугах при построении графа мы указывали планируемое время выполнения работы. Если в следующую вершину входит не одна работа, то мы должны успеть выполнить их все. Кроме того, предыдущее событие тоже требовало от нас каких-то затрат времени.
Поэтому мы прибавляем к тому времени, которое мы уже запланировали потратить, максимальное время, которое мы можем потратить для достижения этого события.
Так делаем для всех событий, соблюдая их очередность.
2. Проставляем позднее время.
В последнем кружочке ставим то же число, что и время раннее для этой вершины. Это время является критическим – т.е. минимально возможное время, за которое возможно выполнить все работы.
Далее начинаем двигаться в обратном направлении: для каждой вершины определяется минимум от позднего времени для предыдущего события и времени выполнения работ, выходящих из данной вершины.
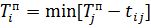
В начальной вершине должен получится 0.
Далее проставляем резерв времени: разница между поздним и ранним временем для каждой вершины.
Полный резерв времени работы: 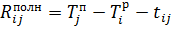
Показывает максимальное время, на которое можно задержать начало или увеличить продолжительность работы без изменения общего срока выполнения работ.
Свободный резерв времени работы: 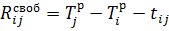
Показывает максимальное время, на которое можно отстрочить начало или увеличить продолжительность работы при условии, что все события наступают в свои ранние сроки.
Так же его можно найти как разницу между полным резервом времени и резервом времени, записанным в кружочке.
Критический путь – путь, длина которого равна критическому времени выполнения проекта. Вдоль критического пути все резервы времени равны 0 (раннее время равно позднему времени в каждой вершине).
Date: 2015-08-15; view: 621; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |