
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Формула Ньютона – Лейбница
Эта формула имеет вид

Эта формула (называемая формулой Ньютона-Лейбница) сводит вопрос о вычислении определенного интеграла любой непрерывной функции к нахождению для нее первообразной функции. По существу этим перекинут мост между двумя частями математического анализа - дифференциальным исчислением (к которому, собственно, надо отнести и понятие первообразной функции) и интегральным исчислением, которое изучает в основном пределы интегральных сумм. К концу XVII в. оба эти исчисления были разработаны уже весьма обстоятельно, но то, что они связаны между собой, еще не было выяснено. Заслугой Ньютона и Лейбница является именно установление факта этой связи. Видим, что в основе ее лежит предложение, составляющее содержание теоремы, почему мы и назвали эту теорему основной теоремой математического анализа.
Ввиду чрезвычайной важности установленного результата придадим ему форму следующего правила:
Правило. Для вычисления определенного интеграла от непрерывной функции надо найти для нее первообразную функцию и составить разность значений этой последней функции при верхнем и нижнем пределах интегрирования.
Здесь 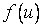 - непрерывная на отрезке
- непрерывная на отрезке  функция, а
функция, а 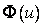 - какая-либо ее первообразная на этом отрезке.
- какая-либо ее первообразная на этом отрезке.
Формула Ньютона – Лейбница была уже доказана в § 6.1. Там предполагалось известным, что непрерывная на  функция
функция 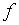 интегрируема и имеет первообразную на
интегрируема и имеет первообразную на  .
.
Теперь мы уже знаем из § 6.3, что интегрируемость непрерывной на  функции влечет за собой существование у нее первообразной на
функции влечет за собой существование у нее первообразной на  .
.
Приведем другое доказательство формулы Ньютона – Лейбница. Вернемся к функции
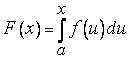 . (2)
. (2)
Заметим, что
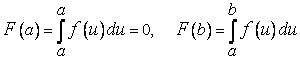 . (3)
. (3)
Кроме того, мы знаем, что 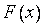 есть первообразная для
есть первообразная для  на
на 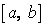 . Поэтому, если
. Поэтому, если  есть какая-либо, вообще другая, первообразная, то существует константа
есть какая-либо, вообще другая, первообразная, то существует константа 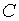 такая, что
такая, что
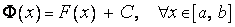 . (4)
. (4)
Из (2), (3), (4) получим
 ,
,
и мы доказали формулу (1).
П р и м е р 1. 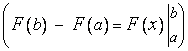
 .
.
Это показывает, что площадь (рис. 78) заштрихованной фигуры, лежащей под параболой  , равна
, равна 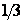 .
.
П р и м е р 2.
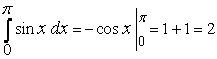 .
.
Таким образом, площадь фигуры (рис. 79), ограниченной сверху синусоидой 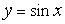 и снизу – осью
и снизу – осью 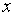 , равна 2.
, равна 2.
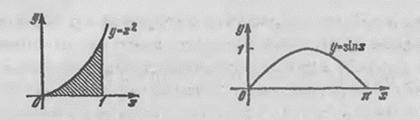
Рис. 78 Рис. 79
П р и м е р 3. Функция

непрерывна на отрезке 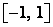 , за исключением точки
, за исключением точки  . Отрезок
. Отрезок 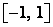 можно разрезать на два отрезка
можно разрезать на два отрезка 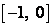 ,
,  , где она монотонна, следовательно, интегрируема. Поэтому
, где она монотонна, следовательно, интегрируема. Поэтому 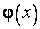 интегрируема на
интегрируема на 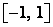 . Справедлива формула
. Справедлива формула
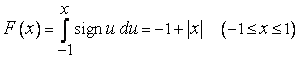 . (5)
. (5)
В самом деле, на полуинтервале 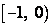 функция
функция 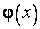 непрерывна:
непрерывна:  . Ее первообразная на этом полуинтервале равна
. Ее первообразная на этом полуинтервале равна 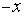 . Поэтому, применяя формулу Ньютона – Лейбница, получим
. Поэтому, применяя формулу Ньютона – Лейбница, получим
 . (6)
. (6)
В силу теоремы 1 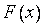 непрерывна, в частности, в точке
непрерывна, в частности, в точке  , поэтому
, поэтому
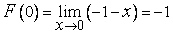 . (7)
. (7)
Для 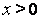
 . (8)
. (8)
Из (6), (7), (8) следует (5).
Более элегантная формула получится, если интегрировать от точки  :
:
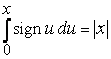 . (9)
. (9)
Под интегралом в (9) стоит разрывная в точке  ограниченная функция, интеграл как функция верхнего предела
ограниченная функция, интеграл как функция верхнего предела 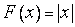 , есть непрерывная функция, в том числе и в точке
, есть непрерывная функция, в том числе и в точке  , что согласуется с теоремой 1 § 6.3. Однако производная
, что согласуется с теоремой 1 § 6.3. Однако производная 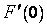 не существует, и это не противоречит теореме 2 § 6.3, которая гарантирует существование производной
не существует, и это не противоречит теореме 2 § 6.3, которая гарантирует существование производной  , только если
, только если 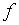 непрерывна в точке
непрерывна в точке 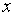 .
.
Т е о р е м а 1 (о замене переменной). Имеет место равенство
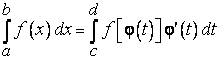 , (10)
, (10)
где функция  непрерывно дифференцируема на
непрерывно дифференцируема на 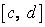 ,
, 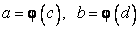 и
и  непрерывна на
непрерывна на 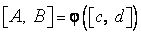 - образе отрезка
- образе отрезка 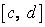 при помощи функции
при помощи функции  .
.
Д о к а з а т е л ь с т в о. Пусть 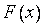 и
и 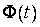 - первообразные функции соответственно
- первообразные функции соответственно  и
и 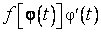 . Тогда (см. § 5.2, (1) и ниже) справедливо тождество
. Тогда (см. § 5.2, (1) и ниже) справедливо тождество 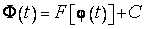 ,
,  , где
, где 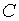 - некоторая постоянная. Поэтому
- некоторая постоянная. Поэтому
 (11)
(11)
Но на основании формулы Ньютона – Лейбница левая часть (11) равна левой части (10), а правая часть (11) – правой части (10), а это доказывает формулу (10).
П р и м е р 4.

 .
.
З а м е ч а н и е. Верхний предел интегрирования по 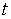 можно взять равным
можно взять равным 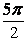 , а результат будет тот же, и это согласуется с теоремой 1.
, а результат будет тот же, и это согласуется с теоремой 1.
П р и м е р 5.
 ,
,
потому что в полученном интеграле нижний предел равен верхнему.
П р и м е р 6. Если 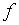 - четная функция
- четная функция 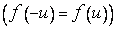 , то
, то
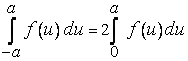 ,
,
потому, что
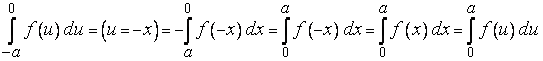 .
.
П р и м е р 7. Если 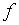 - нечетная функция
- нечетная функция 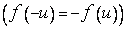 , то
, то
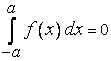 .
.
П р и м е р 8. Если 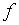 - периодическая функция периода
- периодическая функция периода 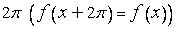 , то
, то
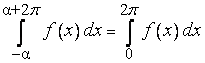
потому, что
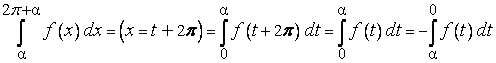 ,
,
и, следовательно,
 .
.
П р и м е р 9.
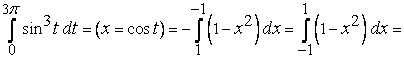
 .
.
П р и м е р 10. Решим пример 5, используя примеры 8, 7:
 ,
,
так как функция 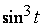 нечетная.
нечетная.
Т е о р е м а 2. Справедлива формула интегрирования по частям для определенного интеграла:
 , (12)
, (12)
где  и
и 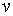 - непрерывно дифференцируемые на
- непрерывно дифференцируемые на  функции.
функции.
Д о к а з а т е л ь с т в о. Произведение 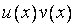 имеет на
имеет на  непрерывную производную
непрерывную производную
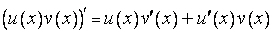 .
.
Поэтому по теореме Ньютона – Лейбница
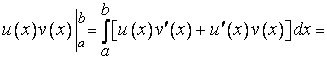
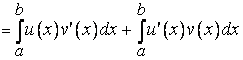 ,
,
откуда следует (12).
П р и м е р (11).
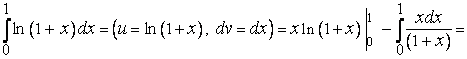
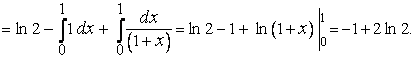
Т е о р е м а 3 (о среднем для определенного интеграла). Для непрерывной на отрезке  функции
функции 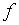 существует точка
существует точка 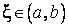 такая, что
такая, что
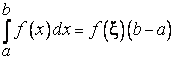 . (13)
. (13)
Д о к а з а т е л ь с т в о. Так как 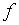 непрерывна, то для нее существует первообразная
непрерывна, то для нее существует первообразная 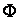 , поэтому
, поэтому
 . (14)
. (14)
Первое равенство в (14) есть формула Ньютона-Лейбница для непрерывной на  функции
функции 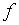 . Второе равенство есть формула Лагранжа для
. Второе равенство есть формула Лагранжа для 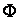 . Наконец третье следует из того, что
. Наконец третье следует из того, что 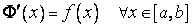 .
.
| <== предыдущая | | | следующая ==> |
| Помни, что невозможно быть успешным, если не можешь себе представить успеха! Мечтай и все у тебя получится! J | | | Протокол выполнения лабораторной работы |
Date: 2015-08-15; view: 558; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |