Виды связи между переменными,

Согласно исследованию научных публикаций в наиболее престижных зарубежных журналах, посвященных социальным и поведенческим наукам (Ч.Теддли, М.Элайс, 2010), 77% всех социологических исследований проведены в рамках количественного подхода. Из них 71% является корреляционными исследованиями или исследованиями, посвященными изучению связей между социальными явлениями.

Самый простой вид корреляционных исследований - изучение парных взаимосвязей или совместной изменчивости двух переменных. Такого рода исследования пригодны для решения двух научных задач:

а) доказательства существования причинно-следственной связи между переменными (наличие связи является важным, но не единственным, условием причинно-следственной зависимости);

б) предсказания: в случае наличия связи между переменными можно с определенным уровнем точности предсказывать значения одной переменной, если нам известно значение другой.

Связь между двумя переменными есть в том случае, когда изменение категории одной переменной ведет к изменению распределения второй:

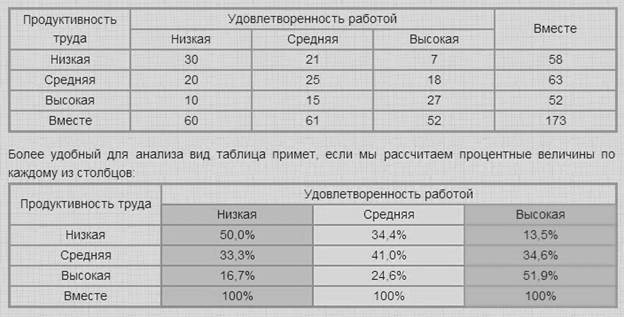
Легко заметить, что в зависимости от категории переменной "Удовлетворенность работой" переменная "Продуктивность труда" меняет свое распределение. Следовательно, мы можем сделать вывод о существовании связи между переменными.

Также из этого примера видно, что каждому из значений одной переменной отвечает несколько значений другой. Такие связи называются статистическими или вероятностными. В данном случае, связь между переменными не является абсолютной. В нашем случае это означает, что кроме удовлетворенности работой есть и другие факторы, влияющие на продуктивность труда.

В случае же, когда одному значению первой переменной соответствует лишь одно значение второй, говорят о функциональных связях. Вместе с тем, даже когда есть основания говорить о функциональной связи, невозможно на все 100% продемонстрировать ее в эмпирической действительности по двум причинам: а) из-за погрешности измерительных инструментов; б) из-за невозможности контроля всех условий окружающей среды, влияющих на эту связь. И поскольку в социальных науках ученые имеют дело именно с вероятностными связями, постольку ниже речь пойдет именно о них.

Парные связи владеют тремя характеристиками: силой, направлением и формой.

Сила показывает насколько согласованна изменчивость двух переменных. Сила связи может изменяться в диапазоне от 0 до +1 (если хотя бы одна из переменных относится к номинальной шкале) или от -1 до +1 (если обе переменные относятся, по крайней мере, к порядковой шкале). При этом 0 и близкие к ней величины говорят об отсутствии связи между переменными, а величины близкие к +1 (прямая связь) или -1 (обратная связь) - о сильной связи. Один из вариантов интерпретации связи, с точки зрения ее силы, выглядит следующим образом:

Все значения в таблице приведены в модуле, т.е. должны анализироваться безотносительно к знаку. Так, например, связь -0,67 и +0,67 являются одинаковыми по силе, но разными по направлению.

Сила связи определяется с помощью коэффициентов корреляции. К коэффициентам корреляции относятся, например, фи и V-крамера (номинальные переменные, мало категорий/табличный вид), Гамма (порядковые переменные, мало категорий/табличный вид), Кендалла и Спирмена (порядковые переменные, много категорий), Пирсона (метрические переменные, много категорий).

Направление говорит о характере взаимного изменения категорий переменных. Если с увеличением значений одной переменной значения другой переменной также увеличиваются, то связь является прямой (или положительной). Если же ситуация противоположная и увеличение значений одной переменной ведет к уменьшению значений второй, то связь обратная (или отрицательная).

Направление связи может иметь место только в тех случаях, когда речи идет о порядковых и/или метрических переменных, то есть тех переменных, значения которых можно упорядочить от меньших к большим или наоборот. Таким образом, если хотя бы одна переменная относится к номинальной шкале, то можно говорить только о силе связи и ее форме, но не о направлении.

Направление связи можно определить либо с помощью таблиц сопряженности (мало категорий), либо с помощью диаграммы рассеяния (много категорий), либо с помощью знака коэффициента корреляции (количество категорий переменных не имеет значения):

А. Определение направления связи с помощью таблицы сопряженности.

Б. Определение направления связи с помощью диаграммы рассеяния.

В. Определение направления связи с помощью коэффициентов корреляции.

Форма связи указывает на особенности совместной изменчивости двух переменных. В зависимости от того, к какой шкале относится переменная, форму связи можно проанализировать либо с помощью столбчатой диаграммы/таблицы сопряженности (если хотя бы одна переменная является номинальной), либо с помощью диаграммы рассеяния (для порядковых и метрических шкал).

Выделяют несколько видов связи между переменными.

· Корреляционная зависимость предполагает взаимную согласованность изменений переменных величин, а также то, что эти изменения можно измерить однократно или многократно (в данном случае говорят о плотности связи переменных, но не о причинно-следственных связях); например, в современном российском обществе чем выше возраст, тем ниже социальный статус человека; отдельные проявления геронтократии эту закономерность не нарушают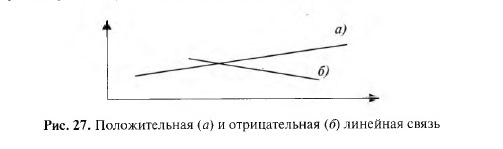

· Функциональное воздействие предполагает, что изменения независимой переменной сопровождаются все более ускоряющимися изменениями зависимой переменной (причинно-следственные связи фиксируют влияние независимой переменной на зависимую); например, чем более радикальными политическими взглядами обладает человек, тем в большей степени он не приемлет существующий политический режим; в то же время нельзя утверждать, что чем в большей степени человек негативно оценивает власть, тем более радикальными взглядами он обладает

· Функциональная зависимость — связь переменных, означающая, что изменение одной переменной оказывает воздействие на изменение другой, которая в свою очередь воздействует на первую переменную, т.е. это связи взаимодействия; например, информированность человека

о политике напрямую связана с интересом к ней; чем больше человек политикой интересуется, тем больше в ней разбирается. Связь может быть нелинейной и немонотонной

Каким бы в итоге ни оказался тип связи между переменными, необходимо убедиться в ее наличии в принципе. Корреляционный анализ применяется для выяснения взаимодействия и тенденций изменения характеристик изучаемого явления.

Корреляция — наличие статистической взаимосвязи признаков, когда каждому определенному значению одного признака X соответствует определенное значение Y (или комплекс значений У-ряда распределения). Корреляционный анализ выясняет функциональную зависимость между переменными величинами, которая характеризуется тем, что каждому значению одной из них соответствует вполне определенное значение другой. Однако корреляционный анализ не предполагает выявления каузальных связей, поэтому при интерпретации результатов формулировки типа «переменная х влияет на переменную у» или «переменная х зависит от переменной у» недопустимы. Различают парную и множественную корреляции. Парная корреляция

характеризует тип, форму и плотность связи между двумя признаками, множественная — между несколькими. Корреляционная зависимость возникает чаще всего там, где одно явление находится под воздействием большого числа факторов, действующих с разной силой, поэтому существуют специальные меры корреляционной связи, называемые коэффициентами корреляции. Коэффициенты (в статистике их общее количество исчисляется десятками) показывают степень взаимосвязи явлений (плотность корреляционной связи, иногда исследователи говорят об интенсивности связи) и характер этой связи (направленность). Связь может быть прямой и обратной. Например, чем старше избиратель, тем более активно он участвует в выборах. Чем выше уровень доходов людей, тем в меньшей степени они склонны участвовать в выборах в качестве избирателей (обратная связь). Чем выше коэффициент корреляции между двумя переменными, тем точнее можно предсказать значения одной из них по значениям другой. Характер связи также определяется в категориях «монотонная» (направление изменения одной переменной не меняется при изменении второй переменной) и «немонотонная» связь. Помимо оценки плотности и направленности связи необходимо учитывать надежность (достоверность) связи.

Корреляционный анализ последовательно решает три практические задачи:

1) определение корреляционного поля и составление корреляционной (в данном случае это комбинированная) таблицы;

2) вычисление выборочных корреляционных отношений или коэффициентов корреляции;

3) проверка статистической гипотезы значимости связи.

44. Корреляционный анализ. Проблема ложной корреляции. Коэффициенты корреляции: виды и условия использования.

Корреляционный анализ применяется для выяснения взаимодействия и тенденций изменения характеристик изучаемого явления.

Первоначальной стадией его развития считается период 1870— 1880-х годов, а автором понятия «коэффициент корреляции» — Фрэнсис Гальтон. Наиболее серьезные разработки в области корреляционного анализа на рубеже XIX-XX вв. выполнил Карл Пирсон. Традиционно корреляционный анализ используется для проверки гипотезы о статистической зависимости двух или нескольких переменных. В качестве вспомогательного средства анализ корреляций можно использовать при проверке пригодности экспериментальных гипотез и для включения переменных в факторный и регрессионный анализ.

Корреляционный анализ осуществляется с помощью сравнения и сопоставления рядов распределения, построенных на основании группировок по различным признакам.

Корреляция — наличие статистической взаимосвязи признаков, когда каждому определенному значению одного признака X соответствует определенное значение Y (или комплекс значений У-ряда распределения). Корреляционный анализ выясняет функциональную зависимость между переменными величинами, которая характеризуется тем, что каждому значению одной из них соответствует вполне определенное значение другой. Однако корреляционный анализ не предполагает выявления каузальных связей, поэтому при интерпретации результатов формулировки типа «переменная х влияет на переменную у» или «переменная х зависит от переменной у» недопустимы. Различают парную и множественную корреляции. Парная корреляция характеризует тип, форму и плотность связи между двумя признаками, множественная — между несколькими. Корреляционная зависимость возникает чаще всего там, где одно явление находится под воздействием большого числа факторов, действующих с разной силой, поэтому существуют специальные меры корреляционной связи, называемые коэффициентами корреляции. Коэффициенты (в статистике их общее количество исчисляется десятками) показывают степень взаимосвязи явлений (плотность корреляционной связи, иногда исследователи говорят об интенсивности связи) и характер этой связи (направленность). Связь может быть прямой и обратной. Например, чем старше избиратель, тем более активно он участвует в выборах. Чем выше уровень доходов людей, тем в меньшей степени они склонны участвовать в выборах в качестве избирателей (обратная связь). Чем выше коэффициент корреляции между двумя переменными, тем точнее можно предсказать значения одной из них по значениям другой. Характер связи также определяется в категориях «монотонная» (направление изменения одной переменной не меняется при изменении второй переменной) и «немонотонная» связь. Помимо оценки плотности и направленности связи необходимо учитывать надежность (достоверность) связи.

Корреляционный анализ последовательно решает три практические задачи:

1) определение корреляционного поля и составление корреляционной (в данном случае это комбинированная) таблицы;

2) вычисление выборочных корреляционных отношений или коэффициентов корреляции;

3) проверка статистической гипотезы значимости связи.

Коэффициент корреляции не содержит информации о том, является ли данная связь между ними причинно-следственной или сопутствующей (порожденной общей причиной).

Для установления корреляционной связи между двумя признаками необходимо доказать, что все другие переменные не оказывают воздействия на отношения двух переменных, являющихся предметом изучения. В противном случае возникает ситуация ложной корреляции. Секрет возникновения ложной корреляции заключается в том, что у двух явлений, связь которых формально подкрепляется наличием статистической связи, есть общая причина, в равной степени влияющая на каждое из них.

Во многих случаях статистически фиксируемая связь между признаками может быть объяснена третьей переменной.

Для выяснения типа связи является перспективным представление данных в виде графика, который позволяет визуально оценить степень рассеяния значений переменных. Особое внимание следует обратить на наличие «выбросов» (экстремально большие или малые значения признака), показывающих существенные отклонения от линии регрессии — условной прямой, которая показывает характер связи между

признаками на графике. Для выяснения факторов, определяющих причинно-следственную связь между переменными, прибегают к пат-анализу. Чтобы избежать ошибки в ситуации ложной корреляции, используют анализ взаимосвязи двух переменных с помощью контрольного (опосредующего) фактора. Итак, корреляционный анализ позволяет отбросить несуществующие или несущественные связи.

Специально следует оговорить, что для получения достоверных данных необходимо обеспечить достаточно большое число наблюдений, поскольку необоснованно сокращая объем выборки, мы снижаем уровень надежности полученных выводов о статистических зависимостях. Следовательно, необходимы специальные знания статистических расчетов. Операции по расчету коэффициентов корреляции осуществляют программы PC, но необходимо хотя бы иметь представление об элементарных процедурах анализа.

Корреляционному анализу предшествует стадия расчета статистики х2- Но на основании полученного значения статистики х2 мы ничего не можем сказать о плотности связи анализируемых переменных.

Для решения такой задачи необходимо обратиться к коэффициентам корреляционной связи.

Различные коэффициенты корреляции могут принимать значения от — 1 до + 1 или от 0 до +1. Специально следует оговорить, что значения коэффициентов, которые принимаются как статистически значимые, значительно разнятся между собой для различных видов коэффициентов корреляции

качестве предварительного замечания отметим, что принято признавать «сверхсильной» связью показатели корреляции свыше |±0,8|, «сильной» — от |±0,6| до |±0,8|, «умеренной» — от |±0,4| до |±0,6|, «слабой» — от |±0,2| до |±0,4|, связь отсутствует при показателях коэффициентов корреляции до |±0,2|. Применительно к значению коэффициента корреляции, приближающемуся к +1, обычно используют обозначение «строгая положительная корреляция» (perfect positive correlation), а к коэффициенту корреляции, равному —1, — «строгая отрицательная корреляция» {perfect negative correlation). А. Бююль и П. Цёфель, а также А. С. Ахременко предлагают несколько иной вариант интерпретации: до |±0,2| — очень слабая корреляция, от |+0,2| до |±0,5| — слабая корреляция, от |+0,5| до 1+0,7| — средняя корреляция, от |±0,7| до |±0,9| — высокая корреляция, свыше |±0,9| — очень высокая корреляция. Отметим, что высокие значения корреляции в реальных политических исследованиях встречаются крайне редко. И действительной исследовательской удачей является обнаружение просто статистически значимого коэффициента корреляции.

Важным показателем оценки коэффициента корреляции является показатель уровня значимости. Для корреляционного анализа он, как и для статистики хи-квадрат, не должен превышать 0,05 (р < 0,05), т.е. вероятность ошибки — подмена устойчивой статистически обоснованной случайной связи — не превышает 5%. Показатель уровня значимости является расчетным, однако как для статистики х2, так и для корреляционного анализа этот показатель формально принимают за константу.

Date: 2015-08-15; view: 12968; Нарушение авторских прав