Полный дифференциал, его нахождение, приложения»

Определение.

Функция 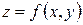называется дифференцируемой в точке (х, у), если ее полное приращение можно представить в виде:

,

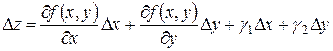где сумма 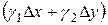– является бесконечно малой высшего порядка относительно

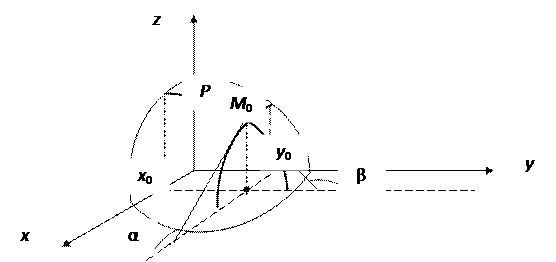
Определение.

Главная часть полного приращения функции, линейная относительно приращений аргументов, называется полным дифференциалом и обозначается через 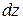или

.

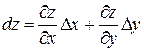Приращения независимых переменных 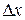и 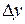мы будем называть дифференциалами независимых переменных и обозначать через dx и dy.

Тогда .

Найти полные дифференциалы функций

1.

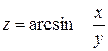
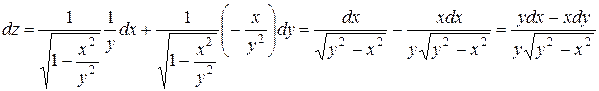
2.

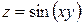
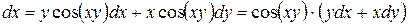
«Частные производные сложной функции»

Пусть z=f(u,v) – дифференцируемая функция.

Пусть при этом u=f₁(x)

v=f₂(x), где f₁(x) и f₂(x) – дифференцируемые функции от аргумента х.

Тогда z=f(f₁(x), f₂(x))=Ф(х) – сложная функция от х.

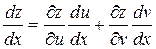(1)

1. Пусть z =F(f₁(x,y), f₂(x,y),

a u=f₁(x,y)

v=f₂(x,y).

Тогда z=F(f₁(x,y), f₂(x,y) – сложная функция двух независимых переменных х и у.

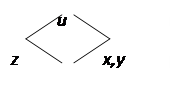Если z=F(u,v), u=f₁(x,y) и v=f₂(x,y) имеют непрерывные частные производные по всем своим аргументам, то

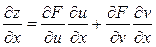
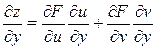
Эти формулы читаются так:

Частная производная сложной функции равна сумме произведений частных производных заданной функции по промежуточным аргументам (u и v) на частные производные этих промежуточных аргументов по соответствующей независимой переменой (х или у).

Типовые задачи, рекомендуемые для решения.

Найти частные производные

1.

u=e^x-2y, где x=sint, y= t³×du/dt

Решение.

Здесь u есть сложная функция одной независимой переменной t.

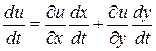
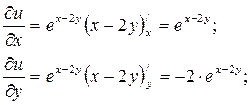
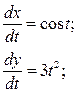
2.

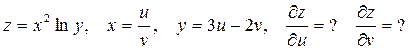
Решение.

z – сложная функция двух переменных u и v.

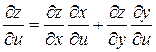
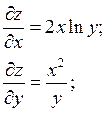
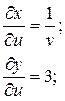
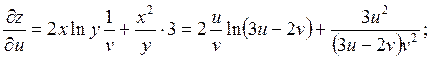
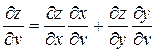
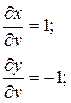
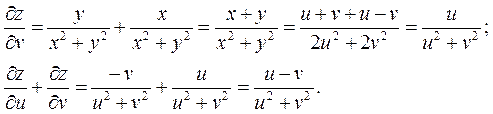
3. z=ln(u²+v²), где u=xcosy, v=ysinx

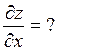
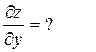
Решение.

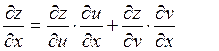
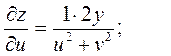
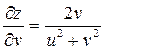
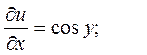
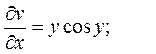
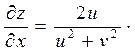
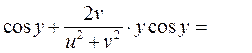
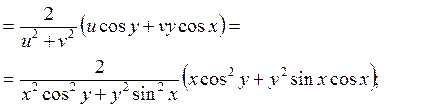
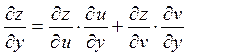
«Полная производная»

Пусть z=F(x,y,u,v),

где у=f₁(x),

u=f₂(x),

v=f₃(x).

Тогда z=F(x,f₁(x), f₂(x),f₃(x)) –я функция независимой переменной х.

–

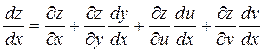– формула для вычисления полной производной.

Полный дифференциал функции z=f(u,v) сохраняется один и тот же вид независимо от того, являются ли ее аргументы u и v независимыми переменными или функциями от независимых переменных.

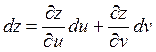
Типовые задачи, рекомендуемые для решения.

Найти полный дифференциал

1.

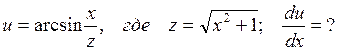
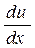– полная производная.

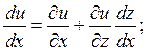
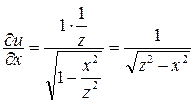, z = const.

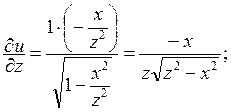x = const.

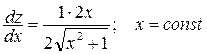
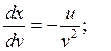
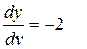
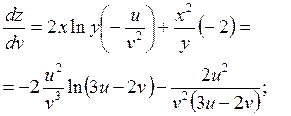
«Частные производные высших порядков»

Частными производными 2-го порядка функции 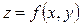называются производные от ее первых производных 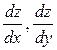, т.е.

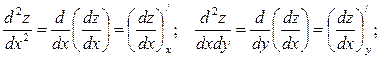
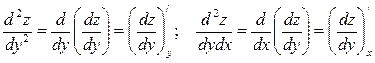
Смешанные производные 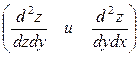, отличающиеся только порядком дифференцирования, равны между собой при условии их непрерывности.

1. .

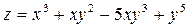Убедиться, что .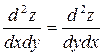

Решение.

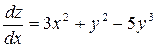
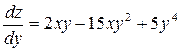
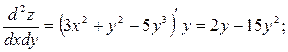
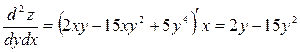
2. .

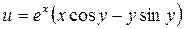Показать, что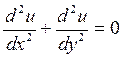

Решение.

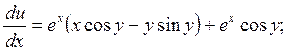
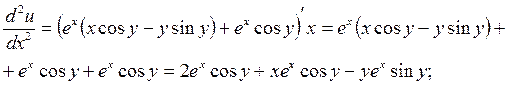
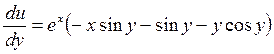
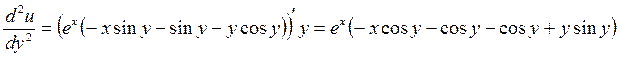
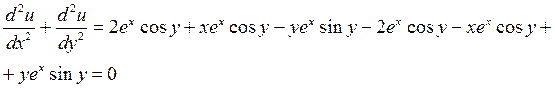
«Необходимое и достаточные условия существования экстремума»

Определение 1. Функция 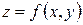в точке 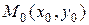имеет максимум, если 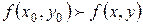для всех точек 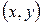, достаточно близких к точке 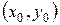и отличных от нее.

Определение 2. Функция 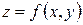в точке 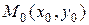имеет минимум, если 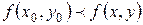для всех точек 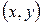, достаточно близких к точке 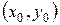и отличных от нее.

Максимум и минимум функции называется экстремумами функции.

Теорема 1. (Необходимые условия экстремума)

Если функция 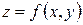в точке 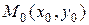имеет экстремум, то каждая частная производная первого порядка от z обращается в нуль при х=х₀, у=у₀ или не существует.

Определение 3. Точки, в которых 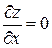(или не существует) и (или не существует), называются критическими точками функции .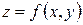

Точка 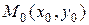, в которой 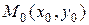и называется стационарной точкой функции .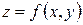

Теорема 2. (Достаточное условие экстремума)

Пусть функция 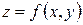непрерывна и имеет непрерывные производные 1-го и 2-го порядков в окрестности точки 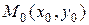и пусть кроме того 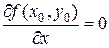и .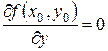

Тогда при х=х₀ , у=у₀:

1. 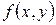имеет max, есл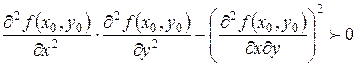и

и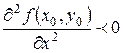

2. 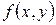имеет min, есл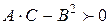и

и .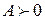

3. f(x, y) не имеет ни max ни min, если

.

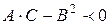4. если 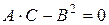, то экстремум может быть и может не быть (требуется дополнительное исследование).

Правило для отыскания наибольшего и наименьшего значений функции 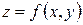в некоторой замкнутой области.

Для того чтобы найти наибольшее и наименьшее значения непрерывной функции 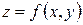в замкнутой области, нужно найти всем максимумы и минимумы этой функции внутри области, а также наибольшее из этих чисел будет наименьшим, наименьшее – наименьшем.

Задача нахождение наибольшего и наименьшего значений функции 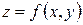на границе области сводится к отысканию наибольшего и наименьшего значений функции одной переменной.

«Нахождение экстремума функции двух переменных»

1. Найти стационарные точки функции:

.

Решение: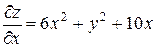

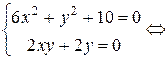
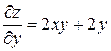
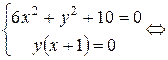
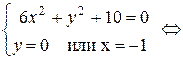
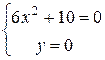или .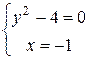

Решаем 1-ую систему: .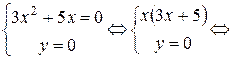

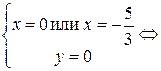
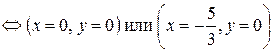Решаем 2-ую систему:

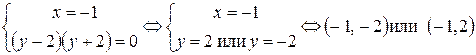
Ответ: (0, 0); 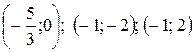– стационарная точка.

2. Найти точки экстремума функции

.

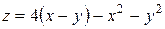Решение: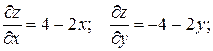

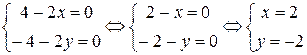
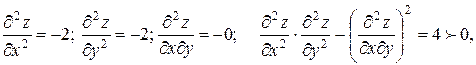
значит (2;–2) – точка экстремума

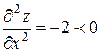, значит (2;–2) – точка max функции.

Date: 2015-08-07; view: 1475; Нарушение авторских прав