Балка на двух шарнирных опорах

2.1. Для балки, на которую действует сосредоточенная нагрузка посредине балки, определить изгибающий момент в любой точке поперечного сечения на левом участке балки проще простого: нужно умножить реакцию одной из опор на расстояние от этой опоры до точки приложения нагрузки (на участке балки от х=0 до х= l/2). В математическом выражении это будет выглядеть так:

М=(Q/2)x (2.1)

Так как в данном случае реакция каждой из опор равна половине от действующей нагрузки. Максимальное значение изгибающего момента также будет посредине, т.е. на расстоянии l/2 от начала балки и будет составлять:

M=(Q/2)(l/2) = Ql/4 (2.2)

Полное уравнение моментов, описывающее равновесие тела или системы, выглядит так:

∑_м= (Q/2)х - Q(х - l/2) + (Q/2)(х - l) =0 (2.3)

Под действием нагрузки и реакции опор на балку действует изгибающий момент, причем значение этого изгибающего момента для каждой точки, а правильнее выражаясь, поперечного сечения балки, разное. В точках опоры изгибающий момент равен 0, вне зависимости от того, где приложена нагрузка, максимальный изгибающий момент действует на балку, когда нагрузка приложена посредине. Для наглядности при решении задач расчета конструкций принято строить "эпюры" изгибающего момента и действующих сил, чтобы потом было проще определить положение поперечного сечения в котором действуют максимальная сила и изгибающий момент. По своей сути эпюры - это графики для функций описываемых соответствующими уравнениями. Например, если нагрузка приложена посредине балки, то эпюры будут выглядеть так:

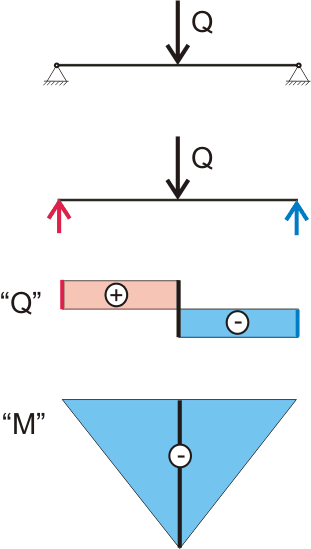
Рисунок №2.1. Эпюры сил и моментов, действующих в поперечных сечениях балки.

Эпюра "Q" отображает изменение сил, действующих на балку, а точнее - изменение касательных напряжений в поперечных сечениях балки. Так по нашей эпюре видно, что вначале балки значение эпюры резко изменяется с 0 на Q/2 - это вступает в действие реакция опоры. Посредине балки, там где приложена сила Q, значение эпюры резко изменяется на величину " Q " и теперь составляет - Q/2, в конце балки в действие вступает вторая реакция опоры равная Q/2, таким образом значение эпюры изменяется с - Q/2 на 0. Знаки "+" и "-" означают направление действия сил. Если сила направлена вверх (параллельно оси у), то такая сила считается положительной, если сила направлена вниз, то такая сила считается отрицательной.

Эпюра "М" отображает изменение изгибающего момента, действующего на балку, а точнее - изменение нормальных напряжений в поперечных сечениях балки (о внутренних напряжениях, нормальных и касательных, речь чуть ниже). Так по нашей эпюре видно, что вначале балки изгибающий момент равен 0 и это логично так как плечо силы, в данном случае опорной реакции, равно нулю, далее значение изгибающего момента увеличивается пропорционально изменению длины плеча силы. Посредине балки, там где приложена сила Q, на эпюре "М" наблюдается перелом, так как в действие вступает еще одна сила - приложенная сосредоточенная нагрузка, которая в 2 раза больше по значению реакции опоры. Далее под действием двух противоположно направленных, приложенных в разных точках и не одинаковых по значению сил значение изгибающего момента уменьшается и в конце балки на правой опоре значение изгибающего момента опять равно 0. По эпюре изгибающих моментов можно визуально определить значение максимального изгибающего момента в поперечном сечении балки. В данном случае все просто и без эпюр вполне можно было бы обойтись, но в дальнейшем, если придется учитывать действие разных нагрузок, в том числе и распределенных, для балки на нескольких опорах или с защемленными концами, наличие правильно построенной эпюры изгибающего момента поможет точно определить положение поперечного сечения балки (и не только балки), в котором изгибающий момент максимальный. Даже без долгих математических расчетов видно, что чем ближе точка приложения нагрузки к середине балки тем больше значение момента и чем ближе точка приложения силы к одной из опор, тем ближе значение момента к нулю и это логично, максимальный момент возникает при максимальном плече действия силы, поэтому при расчете балки на динамические сосредоточенные нагрузки (например по балке будут ходить люди или на балку будет опираться колесо автомобиля) нет необходимости рассчитывать сечение балки при всех положениях нагрузки, достаточно рассчитать балку на нагрузку, приложенную посредине. В данном случае значение момента считается отрицательным, если изгибающий момент пытается вращать балку по часовой стрелке относительно рассматриваемой точки сечения. В некоторых источниках считается наоборот, но это не более чем вопрос удобства. В данном случае по эпюре моментов уже видно, вверх или вниз будет прогибаться балка, без построения эпюр углов поворота и прогибов (об этих эпюрах поговорим чуть позже).

2.2. Если на балку на шарнирных опорах действует не сосредоточенная, а распределенная нагрузка, то эпюры будут выглядеть так:

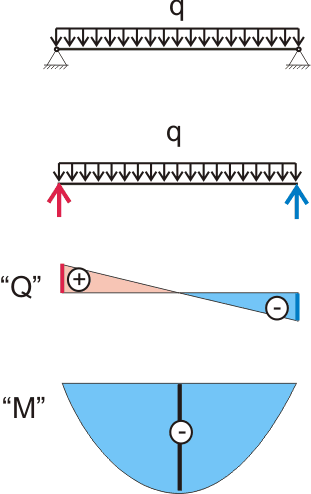
Рисунок №2.2. Эпюры сил и моментов, действующих в поперечных сечениях балки при распределенной нагрузке.

В этом случае, если нагрузка является равно распределенной, то значение максимального изгибающего момента будет составлять

M_max= ql²/ 8 (2.3)

Вывести данную формулу в общем-то несложно. Распределенная нагрузка рассматривается как очень много сосредоточенных нагрузок, приложенных на одинаковом расстоянии друг от друга. Далее для каждой нагрузки можно построить свою эпюру изгибающих моментов, а потом эти эпюры сложить или сразу строить эпюру, учитывающую действие сосредоточенных нагрузок. Чем больше будет сосредоточенных нагрузок, тем менее ломаным будет низ эпюры. Чтобы каждый раз не рисовать огромное количество эпюр используется интегральное вычисление, для этого его и придумали. Так как у нас на правой или на левой половине балки действуют две силы: рекция опоры и распределенная нагрузка, то значение изгибающего момента в некотором поперечном сечении балки можно определить, решив уравнение:

М = (ql/2)х - (qх)х/2 (2.3а)

в данном случае значение распределенной нагрузки сначала сводится к сосредоточенной нагрузке, действующей на некотором участке х, а затем умножается на плечо силы х/2. Таким образом посредине балки значение изгибающего момента будет составлять:

М = (ql/2)l/2 - (ql/2)l/(2·2) = ql²/4 -ql²/8= ql²/8 (2.3b)

В математике такая операция называется интегрированием уравнения в пределах от 0 до l/2. А это значит, что сосредоточенная нагрузка, действующая на балку, это производная изгибающего момента. Если еще раз посмотреть на построенные нами эпюры, то мы увидим, что, действительно, значение максимального изгибающего момента (посредине балки) равно площади прямоугольника эпюры "Q" (рисунок №2.1) или площади треугольника эпюры "Q" (рисунок №2.2). Кроме того сосредоточенная нагрузка - это производная равно распределенной нагрузки и таким образом равно распределенная нагрузка - это вторая производная изгибающего момента, а в свою очередь изгибающий момент - это вторая производная от величины прогиба балки (первая производная от величины прогиба - это угол поворота), и, значит, что все эти эпюры сил, моментов, углов поворотов и прогибов конструкции (здесь не приводятся) тесно связаны между собой, но не будем углубляться в теорию, хотя для меня в свое время это было чуть ли не первое наглядное применение совершенно абстрактных в школьную пору интегралов и производных. Вот такая математика.

Конечно же, вариантов нагрузок, приложения нагрузок, количества опор, видов опор и, соответственно, вариантов построения эпюр -великое множество, но для решения простых задач по расчету строительных конструкций в подробном рассмотрении других вариантов нет необходимости, хотя еще один пример все же приведу (для более логичного перехода к следующим положениям сопромата).