Пояснение 2

Пусть у нас есть прямая A, пересекающая некоторую прямую C под тем же углом, что и прямая B. (как показано на рисунке) – тогда A и B – параллельны.

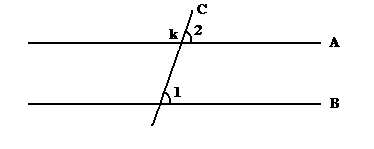
рисунок 24

Доказательство этого утверждения (1) Евклид проводит без обращения к одиннадцатой аксиоме. Аналогичное утверждение есть и в геометрии Лобачевского. (2)

Одиннадцатая же аксиома гласит, что если прямые пересекают C под разными – внешним и внутренним по одну сторону углами, угол1 ≠ угол2, то продолжаясь они обязательно встретятся (не параллельны). (3) *

рисунок 27

*Пояснение к аксиоме. У Евклида это формулируется так: < И если прямая, падающая на две прямые, образует внутренние по одну сторону углы, меньшие двух прямых (4), то продолженные эти две прямые неограниченно встретятся с той стороны, где углы меньше двух прямых >.

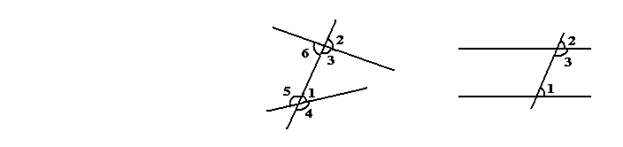
рисунок 28

Понятно, что в случае если с какой то стороны внутренние по одну сторону углы меньше двух прямых: угол1 + угол3 < 2∟, то так как угол1 + угол5 = 2∟ и угол3 + угол6 = 2∟, то угол1 + угол3 + угол5 + угол6 = 4∟ а угол1 + угол3 < 2∟ значит - угол5 + угол6 > 2∟. То есть с другой стороны углы больше двух прямых.

Также так как угол1 + угол3 < 2∟ и угол2 + угол3 = 2∟ то угол1 < угол2. (внешний больше внутреннего)

И так как угол1 + угол3 < 2∟ и угол1 + угол4 = 2∟ то угол3 < угол4.

И наоборот, если угол1 = угол2, то раз угол2 + угол3 = 2∟ значит и угол1 + угол3 = 2∟, а так как угол1 + угол3 + угол5 + угол6 = 4∟, то и угол5 + угол6 = 2∟.

Теперь ясно, что если параллельные и пересекаются некоторой прямой, то пересекаются ею под одинаковыми (внешним и внутренним с одной стороны) углами, ибо согласно одиннадцатой аксиоме если эти углы не будут равны, то продолжаясь, прямые встретятся, а данные прямые параллельны.

В геометрии, названной Лобачевским – воображаемой, роль одиннадцатой аксиомы выполняет непохожее утверждение. Пусть линии геометрии Лобачевского [2.1] образуют такую фигуру:

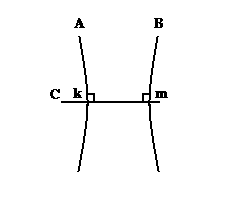
рисунок 29

тогда согласно аналогу одиннадцатой аксиомы действующему в геометрии Лобачевского (согласно этому непохожему на одиннадцатую аксиому утверждению) через точку k (тоже справедливо и для точки m) можно провести ещё и другие линии Лобачевского (кроме «линии» A) не пересекающие «линию» B. Все они располагаются так. Через точку k под углом α к «линии» С (как показано на рисунке) проходят ещё две «линии» не пересекающие «линию» B

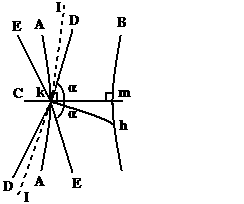
рисунок 30

– E и D – они (эти две особые «линии» - не пересекают «линию» B). Также, (согласно утверждению аналогичному девятой аксиоме (см. пояснение [2.1])) «линию» B не пересекают и все другие «линии» проходящие через точку k и лежащие между «линиями» E и D. При этом «линии» E и D в геометрии Лобачевского называются параллельными «линии» B, а все лежащие между ними – просто не пересекающими «линию» B. (в геометрии Лобачевского в понятие параллельных «линий» вкладывается несколько иной смысл.) Все же «линии» проходящие через точку k, под углом к «линии» С – меньшим, чем α, (как, например, «линия» kh) – пересекают «линию» B. [2.2]

Теперь, продолжая говорить о свойствах линий Лобачевского, вспомним о двух очень важных теоремах общей геометрии (абсолютной геометрии) (5). Первая из них это теорема о сумме углов треугольника (общей геометрии): сумма углов треугольника не может быть больше двух прямых углов. (не может быть больше π) Вот её доказательство: возьмём некоторую неограниченную линию A и постоем на ней один и тот же треугольник несколько раз (как на рисунке)

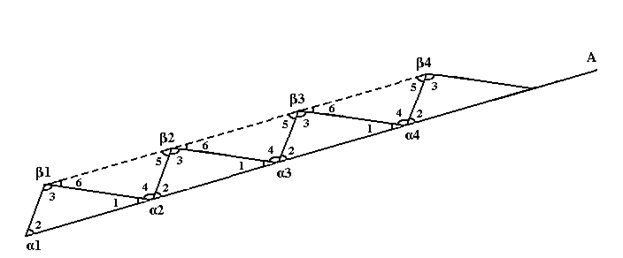
рисунок 31

тогда если сумма углов треугольника (α1 β1 α2) (далее ∑∆(α1 β1 α2)) > 2∟ то так как угол1 + угол2 + угол4 = 2∟, а угол1 + угол2 + угол3 > 2∟ → угол4 < угол3. Рассмотрим два треугольника ∆(α1 β1 α2) и ∆(β2 α2 β1)

β2α2 = α1β1, β1α2 = α2β1, угол4 > угол3

Значит согласно двадцать четвёртому предложению Начал (6): < Если два треугольника имеют две стороны, равные двум сторонам каждая каждой, но заключённый между равными сторонами угол > в одном < больше, > чем в другом <, то и основание > в первом < будет больше основания > во втором. – линия β1β2 меньше линии α1α2. Пусть величина на которую α1α2 больше β1β2 будет γ. Тоже касается и сторон α2α3 и β2β3: α2α3 больше β2β3 на ту же величину γ. – а значит и всех последующих отрезков α3α4 > β3β4 так что β3β4 + γ = α3α4, β4β5 + γ = α4α5 и так далее.

Значит линия α1αn больше суммы отрезков β1β2 + β2β3 + β3β4 + … + βn-1βn на величину γ взятую n раз. А так как всякую величину можно взять столько раз чтобы она превосходила заданную, то возьмём γ столько раз, чтобы она превосходила α1β1 и αnβn взятые вместе (или что то же самое α1β1 взятую дважды.)

Тогда β1β2 + β2β3 + β3β4 + … + βn-1βn + γ*n = α1αn (здесь * - знак умножения)

а так как γ*n > α1β1 + αnβn то

β1β2 + β2β3 + β3β4 + … + βn-1βn + α1β1 + αnβn < α1αn

Значит мы имеем цепочку отрезков.

α1β1 ↔ β1β2 ↔ β2β3 ↔ β3β4 ↔ … ↔ βn-1βn ↔ βnαn ↔ αnα1

Где β1β2 + β2β3 + β3β4 + … + βn-1βn – ломанная линия. Причём α1β1 + β1β2 + β2β3 + β3β4 + … + βn-1βn + βnαn < α1αn. (то есть одно из звеньев (α1αn) больше всей остальной цепочки) Значит согласно двадцатому предложению Начал: < Во всяком треугольнике две стороны, взятые вместе при всяком их выборе, больше оставшейся > и в треугольнике α1β1β2 α1β1 + β1β2 > α1β2. А значит и ломанная α1β2 + β2β3 + β3β4 + … + βn-1βn + βnαn меньше ломанной α1β1 + β1β2 + β2β3 + β3β4 + … + βn-1βn + βnαn и уж подавно значит меньше линии α1αn. Подобным же образом докажем и что α1β3 + β3β4 + … + βn-1βn + βnαn меньше α1αn и что α1β4 + β4β5 + … + βn-1βn + βnαn меньше α1αn и так далее. Значит α1βn + βnαn < α1αn что противоречит двадцатому предложению Начал. (которое как и двадцать четвёртое предложение относится к общей геометрии). Значит сумма углов треугольника не может быть больше двух прямых углов. Надо заметить, что предположения ∑∆(α1β1α2) < 2∟ и ∑∆(α1β1α2) = 2∟ не будут приводить к такому противоречию. В первом случае: так как угол1 + угол2 + угол4 = 2∟, а угол1 + угол2 + угол3 < 2∟, то угол4 > угол3, а значит β1β2 > α1α2 и противоречия не возникает. Не возникает его и во втором случае угол1 + угол2 + угол3 = 2∟ → угол4 = угол3 → β1β2 = α1α2. Другое доказательство этой теоремы приводит Лобачевский в самом начале своей работы – Геометрические исследования по теории параллельных линий – предложение 19.

Вторая теорема, которую мы здесь докажем гласит, что если сумма углов некоторого треугольника равна двум прямым (7), то и сумма углов любого другого треугольника также равна двум прямым. Отсюда конечно ясно, что если сумма углов какого-то треугольника меньше двух прямых (что она не может быть больше мы уже доказали) то и сумма углов любого другого треугольника тоже меньше двух прямых ибо если бы нашёлся хоть один треугольник имеющий сумму углов – два прямых, то и любой бы другой треугольник, также имел бы такую сумму углов. Поэтому докажем первое утверждение. Пусть у нас есть некоторый треугольник сумма углов которого – два прямых. Докажем сначала, что у всякого треугольника должны быть два острых угла – тоесть два угла, каждый из которых меньше прямого. Пусть

рисунок 32

- сумма углов треугольника. Тогда, если один из углов тупой (больше прямого) – случай А

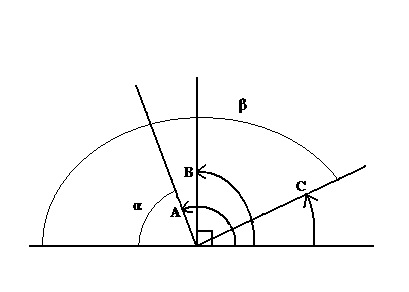
рисунок 33

то понятно, что каждый из двух оставшихся будет острый ибо даже в сумме оставшиеся составляют острый угол. (угол α) Если же один из углов прямой (случай B) то каждый из двух оставшихся будет острый (меньше прямого) ибо в сумме оставшиеся составляют прямой, а значит каждый из них должен быть меньше прямого (быть острым). И наконец если один из углов треугольника острый (случай C), то оставшийся угол β – меньше двух прямых, и значит как не разделяй его на две части – хотя бы одна из частей будет меньше прямого угла (то есть будет острым углом). Ибо невозможно из двух частей, каждая из которых больше или равна прямому (не острая) составит целое меньшее двух прямых. Значит во всяком треугольнике, сумма углов которого два прямых должны быть хотябы два острых угла. Подобным же образом можно доказать, что и во всяком треугольнике, сумма углов которого меньше двух прямых также должно быть хотя бы два острых угла. Значит во всяком треугольнике есть два острых угла. Это предварительное доказательство нам нужно было провести, чтобы разделить наш исходный треугольник (сумма углов которого - два прямых) на два прямоугольных треугольника. Для этого рассмотрим ту сторону треугольника, которая соединяет его острые углы A и B и из вершины ей противолежащей С опустим на неё перпендикуляр (8) (двенадцатое предложение Начал). Теперь благодаря нашему предварительному доказательству мы знаем, что опущенный перпендикуляр упадёт на неограниченную линию E между точками A и B.

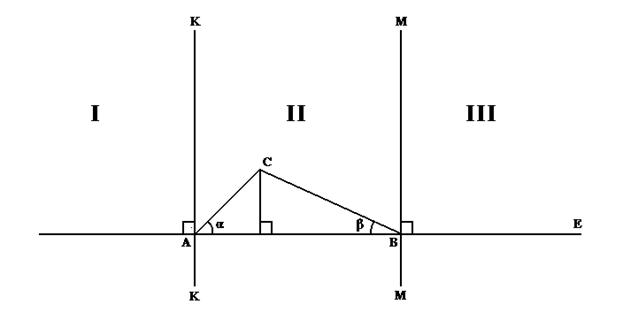
рисунок 34

Где α и β –острые углы.

Ибо перпендикуляры проведённые из точек A и B к неограниченной линии E делят всю плоскость на три части I, II и III. А так как точка C принадлежит части II (это видно из того, что углы α и β – острые), то перпендикуляр из неё опущенный, должен упасть на неограниченную линию E между точками A и B так как в противном случае мы бы имели перпендикуляр – восставленный из некоторой точки, которая пренадлежит неограниченной линии E, но не принадлежит отрезку AB – проходящий через точку C – а значит пересекающий один из перпендикуляров (K или M) – чего не может быть в силу того, что перпендикуляры к некоторой линии (линии E) не могут пересекаться

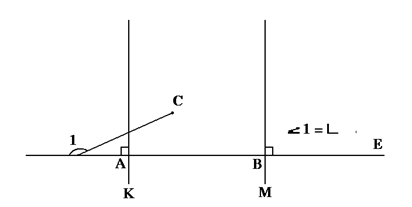
рисунок 35

Значит мы разделили наш треугольник ABC, сумма углов которого два прямых, на два прямоугольных треугольника ADC, DBC.

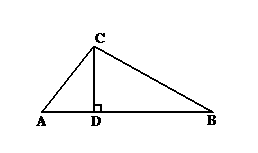
рисунок 36

Но если мы произвольным образом разбиваем некоторый треугольник на два других, то если сумма углов этого треугольника два прямых, то и сумма углов каждого из двух его составляющих также будет два прямых. Это видно из следующего рисунка:

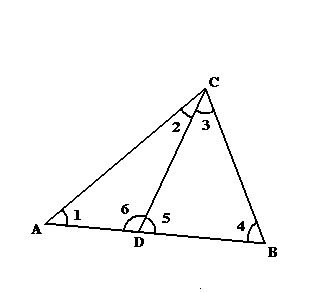
рисунок 37

Пусть ∑∆ABC = 2∟, тогда, угол1 + угол2 + угол3 + угол4 + угол5 + угол6 = 4∟(так как угол1 + угол2 + угол3 + угол4 = ∑∆ABC = 2∟, а угол5 + угол6 = 2∟), но угол1 + угол2 + угол3 + угол4 + угол5 + угол6 = (угол1 + угол2 + угол6) + (угол3 + угол4 + угол5) = ∑∆ADC + ∑∆DBC, значит ∑∆ADC + ∑∆DBC = 4∟. Значит не может быть, чтобы сумма углов хотя бы одного из этих треугольников ADC и DBC была меньше двух прямых – значит ∑∆ADC= 2∟ и ∑∆DBC= 2∟.

Справедливо и обратное утверждение: если некоторый треугольник – ABC разбит на два треугольника ADC и DBC сумма углов каждого из которых два прямых, то и сумма углов этого треугольника (ABC) также два прямых.

Пусть ∑∆ADC= 2∟ и ∑∆DBC= 2∟ (тот же рисунок) тогда угол1 + угол2 + угол6 = 2∟ и угол3 + угол4 + угол5 = 2∟. Значит угол1 + угол2 + угол6 + угол3 + угол4 + угол5 = 4∟, но угол5 + угол6 = 2∟ тогда вычтем из правой части два прямых, а из левой угол5 + угол6, и получим угол1 + угол2 + угол3 + угол4 = 2∟, но угол1 + угол2 + угол3 + угол4 = ∑∆ABC, значит ∑∆ABC = 2∟.

Возвращаясь к нашему треугольнику имеющему сумму углов два прямых и разделённому на два прямоугольных треугольника мы получаем, что каждый из этих прямоугольных треугольников имеет сумму углов два прямых. Значит если мы имеем некоторый произвольный треугольник имеющий сумму углов два прямых, то мы имеем и два прямоугольных треугольника, каждый из которых имеет сумму углов – два прямых. Возьмём один из этих прямоугольных треугольников (пусть например это будет треугольник ADC)

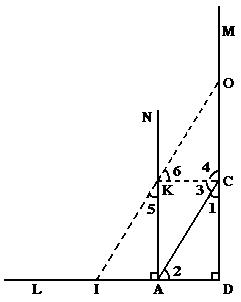
рисунок 38

и построим на нём равный ему треугольник AKC например так: восставим из точки A перпендикуляр AN (как на рисунке) и отложим на нём AK = DC, тогда так как угол1 + угол2 = ∟ (так как ∑∆ ADC = 2∟) то угол1 = ∟ - угол2 угол же KAD = ∟ значит угол KAC = ∟ - угол2, значит угол1 = уголKAC.

Теперь рассмотрим два треугольника: ∆ KAC и ∆DCA KA = DC по построению, угол1 = уголKAC, AC же общая, значит согласно четвёртому предложению Начал: < Если два треугольника имеют по две стороны, равные каждая каждой, и по равному углу, содержащемуся между равными прямыми, то они будут иметь и основание, равное основанию, и один треугольник будет равен другому, и остальные углы, стягиваемые равными сторонами, будут равны остальным углам каждый каждому. > - ∆ KAC = ∆DCA → KC = DA, уголACK = угол2, уголAKC = уголCDA = ∟. Значит мы постоили на треугольнике ADC равный ему треугольник. Теперь зная, что угол3 = угол2, а угол2 + угол1 = ∟, мы знаем, что и угол3 + угол1 = угол4 = ∟. Тогда постоим ещё два треугольника равных ADC: ∆IAK и ∆KCO, отложив на DL IA = AD и на DM отложив OC = CD. (∆IAK = ∆ADC (по четвёртому предложению Начал) так как уголIAK = уголADC = ∟, IA = AD, AK = DC, также и ∆KCO = ∆ADC). угол5 же равен угол1, угол6 = угол2, значит угол5 + угол6 = угол1 + угол2 = ∟, значит угол5 + угол6 + уголAKC = 2∟, так как уголAKC = ∟. Таким образом имея прямоугольный треугольник мы построили на нём другой прямоугольный треугольник каждая сторона которого вдвое больше каждой (соответствующей) стороны прежнего, причём сумма углов нового треугольника также равна двум прямым (так как уголAIK = угол2, а уголIOD = угол1). Продолжая построение можно построить сколь угодно большой (9) прямоугольный треугольник сумма углов которого будет два прямых (каждый раз удваивая построенный). Значит, имея первоначально произвольный треугольник, сумма углов которого равна двум прямым, мы можем построить сколь угодно большой прямоугольный треугольник с такой же суммой углов.

Теперь благодаря тому, что мы можем построить любой сколь угодно большой прямоугольный треугольник с суммой углов два прямых, можно и для любого произвольно взятого и произвольно расположенного прямоугольного треугольника – доказать, что его сумма углов также два прямых – следующим образом: пусть у нас есть некоторый произвольно взятый и произвольно расположенный прямоугольный треугольник O1O2O3. Построим такой большой прямоугольный треугольник ABC, с суммой углов два прямых, чтобы его наименьшая сторона

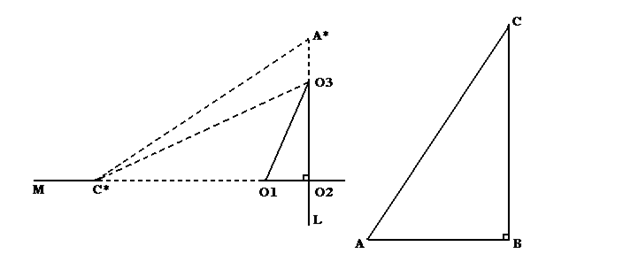
рисунок 39

AB превысила наибольший из катетов треугольника O1O2O3, - отрезок O3O2. Значит поскольку AB > O3O2, а BC > AB, то BC > O3O2, а так как O3O2 – наибольший катет то O3O2 > O1O2, значит BC > O1O2, значит, AB > O3O2 BC > O1O2. Теперь построим треугольник A*O2C* равный треугольнику ABC так, чтобы он включал треугольник O1O2O3, а именно на неограниченной линии L отложим O2A* = BA, а на неограниченной линии M отложим O2C* = BC (как показано на рисунке). И соединим C*A*. Треугольник A*O2C* равен треугольнику ABC согласно четвёртому предложению Начал. (O2A* = BA, уголA*O2C* = O3O2O1 = ∟ = угол ABC, O2C* = BC) и значит также как и треугольник ABC имеет сумму углов два прямых, кроме того он заключает треугольник O1O2O3 так как O2A* = BA, а BA > O3O2; O2C* = BC, а BC > O1O2. А так как ∑∆ (A*O2C*) = 2∟, значит ∑∆ (O3O2C*) = 2∟, а значит и ∑∆ (O1O2O3) = 2∟ (так как мы уже доказали, что если треугольник, сумма углов которого – два прямых – разбит на два треугольника, то сумма углов каждого из этих треугольников – также равна двум прямым.) Значит для любого произвольно взятого и произвольно расположенного прямоугольного треугольника можно доказать, что его сумма углов равна двум прямым – значит и для любого вообще треугольника можно доказать, что его сумма углов равна двум прямым, ибо любой вообще треугольник можно разбить на два прямоугольных треугольника (а мы уже доказали, что если некоторый треугольник, разбит на два треугольника, сумма углов каждого из которых – два прямых, то и сумма углов этого треугольника также – два прямых.)

Значит, если сумма углов некоторого треугольника равна двум прямым, то и сумма углов любого другого треугольника (произвольно взятого и произвольно расположенного) также равна двум прямым. А значит и если сумма углов какого то треугольника меньше двух прямых, то и сумма углов любого другого треугольника – меньше двух прямых. Это доказательство с незначительными изменениями взято из сочинения Н. И. Лобачевского - «Геометрические исследования по теории параллельных линий» - предложение 20.

Докажем теперь ещё одну важную теорему: сумма углов всякого прямолинейного треугольника (треугольника образованного прямыми) равна двум прямым.

Для доказательства этой теоремы обратимся к теореме полученной из одиннадцатой аксиомы в самом начале этого примечания: если некоторая прямая и пересекает параллельные прямые, то пересекает их под одинаковыми – внешним и внутренним по одну сторону углами.

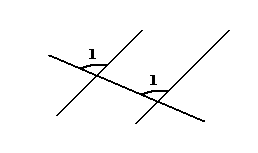
рисунок 40

Рассмотрим треугольник ABC и продолжим его стороны – как показано на рисунке – неограниченно. Построим теперь неограниченную прямую K, пересекающую неограниченную прямую D в точке B под тем же углом, что и неограниченная прямая L в точке A.

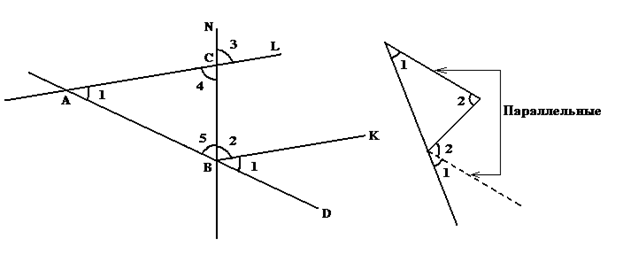
рисунок 41

Тогда K и L не имеют общей точки (параллельны) – Значит неограниченная прямая N пересекает параллельные прямые – значит пересекает их под одинаковыми углами: угол2 = угол3, а так как угол3 = угол4 (пятнадцатое предложение Начал) то угол2 = угол4.

Но угол1 + угол5 + угол2 = 2∟, а так как угол2 = угол4 то угол1 + угол5 + угол4 = 2∟

Но угол1 + угол5 + угол4 = ∑∆ABC → ∑∆ABC = 2∟.

Это доказательство – взятое с незначительными изменениями – (касающимися скорее изложения, нежели самой идеи доказательства) – тридцать второе предложение Начал. Там также доказывается, что внешний угол равен сумме двух внутренних ему противолежащих то есть на нашем рисунке угол1 + угол2 = угол1 + угол4. Это ясно из того, что угол2 = угол4. У Евклида эта теорема формулируется так: < Во всяком треугольнике по продолжении одной из сторон внешний угол равен двум внутренним и противолежащим, и внутренние три угла треугольника > вместе <равны двум прямым>. Второй рисунок тоже поясняет смысл этого доказательства. Докажем теперь, опираясь на эту теорему одиннадцатую аксиому Евклида. Прежде чем провести доказательство, докажем из одиннадцатой аксиомы и обратно следующее утверждение: через точку не лежащую на прямой можно провести одну и только одну прямую параллельную данной. Справедливость этого утверждения ясна из следующего. Возьмём на рассматриваемой прямой B некоторую точку D и соединим её с рассматриваемой, не лежащей на прямой точкой K. (как показано на рисунке) – прямой DK.

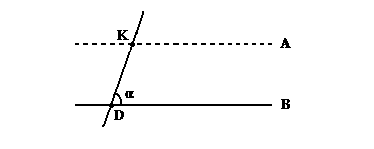
рисунок 42

Пусть угол пересечения этих прямых будет α. Очевидно, что из всех прямых проходящих через точку K, только одна проходит под тем же углом к прямой DK, что и прямая B (под углом α) остальные же под отличными от него углами. Значит эта прямая параллельна прямой B (согласно двадцать седьмому предложению Начал)*, остальные же, пересекая прямую DK не мод тем же углом, что и прямая B, пересекают и прямую B согласно одиннадцатой аксиоме. Значит из всех прямых проходящих через точку K не лежащую на прямой B одна и только одна параллельна данной прямой.

* Ещё раз возвращаясь к двадцать седьмому предложению Начал приведу его здесь: < Если прямая падающая на две прямые, образует накрестлежащие углы, равные между собой, то прямые будут параллельны друг другу >

Это можно проиллюстрировать следующим рисунком –

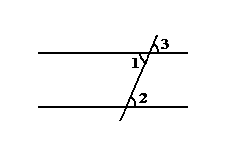
рисунок 43

-если угол 1 равен углу 2, то прямые параллельны, или, что тоже самое (пятнадцатое предложение Начал) если угол1 = угол3 то прямые параллельны. Евклид в Началах даёт этому предложению очень интересное доказательство восходящее (как я уже упоминал) к предложению 16 и предложению 4. Однако я думаю эта теорема может быть обоснована и из следующих соображений: пусть некоторую прямую, пересекают две другие (CE и DF) под равными (внешним и внутренним по одну сторону) углами. (как показано на рисунке)

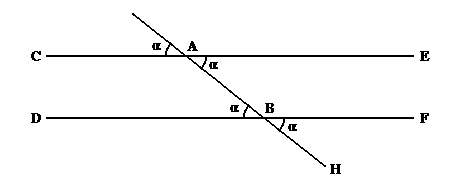
рисунок 44

Продолжим прямую AB неограниченно (обозначим эту неограниченную прямую H). Тогда мы имеем неограниченную прямую и восставленные на ней под одинаковыми углами (равными α) прямые BF и AE.

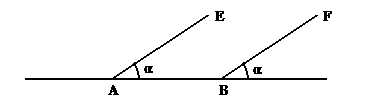
рисунок 45

Если же, продолжаясь, они пересекутся, то значит, продолжаясь, пересекутся и прямые AC и BD восставленные на неограниченной прямой под одинаковыми, также равными α углами. Если же и они, продолжаясь пересекаются, то прямые CE и DF продолжаясь каждая в обе стороны, пересекутся дважды и заключат пространство, что невозможно. Значит, если некоторую прямую, пересекают две другие, под равными, (внешним и внутренним по одну сторону) углами, то эти прямые параллельны. Похожим образом эта теорема обосновывается в комментариях к первой книге Начал принадлежащих Д. Д. Мордухай – Болтовскому (эти комментарии входят в используемое издание Начал: НАЧАЛА ЕВКЛИДА КНИГИ I – VI Перевод с греческого и комментарии Д. Д. Мордухай – Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского Государственное издательство технико – теоретической литературы Москва · Ленинград · 1950.) Там обоснование данной теоремы сходное с этим помещено в комментарии пятьдесят восьмом и называется – «Приём Ома», и дана ссылка – Ohm, Ebene Raumwissenschaft, 2 Aufl., Berlin, 1835, §26, стр. 111.

Также, почти идентичное данному обоснование дано в книге Прокла Диадоха «Комментарии к первой книге «Начал»» в самом начале «раздела» Предложения: Часть 2. Прокл ссылается на некого Птолимея и начинает собственно само доказательство со слов: «А Птолимей в книге, где он пытается доказать, что прямые образующие углы…» Прокл Диадох Перевод А. И. Щетникова.

Теперь, возвращаясь к нашему доказательству, проведём и обратное – из утверждения, что через точку не лежащую на прямой проходит одна и только одна прямая, параллельная данной, докажем одиннадцатую аксиому. Значит пусть у нас есть некоторая прямая B, пересекаемая прямой C под углом 1 (угол1) как показано на рисунке (в точке D)

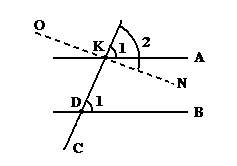
рисунок 46

Возьмём на прямой C некоторую точку K. И проведём через неё прямую A, под тем же углом к прямой С, что и прямая B. Значит она (прямая A) параллельна прямой B. Через точку же не лежащую на прямой, проходит только одна прямая параллельная данной. Значит прямая A единственная прямая проходящая через точку K и параллельная B. Она же проходит через точку K под тем же углом к прямой C, что и прямая B, через точку D. Значит среди всех, прямых проходящих через точку K под углом (к прямой C) отличным от угла 1 нет ни одной параллельной по отношению к B (ибо единственная проходящая через точку K, параллельная B прямая, проходит через неё под углом к прямой C, равным углу 1). Значит все, прямые проходящие через точку K под углом (к прямой С) отличным от угла 1 пересекают (не параллельны) прямую B.

Примечание же, «3» данное мной к одиннадцатой аксиоме не требует отдельного доказательства, так как доказывается из самой одиннадцатой аксиомы. Действительно возьмём некоторую прямую OKN проходящую через точку K под углом 2, причём угол2 > угол1. Ясно, что продолжаясь в обе стороны прямая OKN пересечёт неограниченную прямую B со стороны KN, так как продолжаясь в сторону KO прямая OKN не может пересечь B в силу девятой аксиомы.

Значит из утверждения, - что через точку не лежащую на прямой, можно провести одну и только одну прямую параллельную данной - можно доказать одиннадцатую аксиому и обратно. Значит доказав это утверждение мы докажем и одиннадцатую аксиому. Мы же хотели доказать одиннадцатую аксиому из утверждения, что сумма углов всякого треугольника два прямых. (или что то же самое из утверждения, что сумма углов некоторого треугольника два прямых угла, ибо как уже доказано, если сумма углов некоторого треугольника два прямых, то и сумма углов всякого треугольника – два прямых.)

Итак мы знаем, что сумма углов всякого прямолинейного треугольника два прямых, докажем отсюда одиннадцатую аксиому, доказав, что через точку не лежащую на прямой проходит одна и только одна прямая параллельная данной. Пусть у нас есть некоторая неограниченная прямая B и не лежащая на ней точка K. Опустим на прямую B из точки K перпендикуляр (двенадцатое предложение Начал). Теперь через точку K проведём ещё одну неограниченную прямую (прямую A) перпендикулярно опущенному перпендикуляру (как на рисунке)

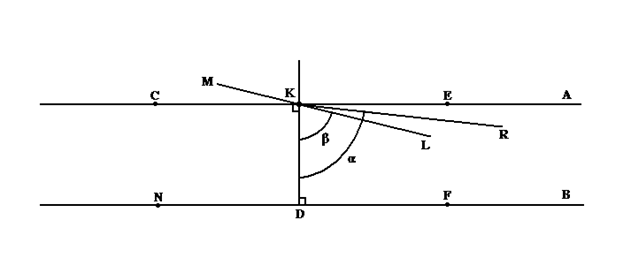
рисунок 47

Докажем, что все другие прямые проходящие через точку K пересекают прямую B. Отложим на прямых A и B по одну сторону от перпендикуляра соответственно точки E и F, а пор другую сторону, соответственно C и N. Ясно, что всякая прямая (10) проходящая через точку K проходит либо через угол CKD либо через угол EKD. Рассмотрим угол EKD (то же самое будет и для угла CKD) и докажем, что все прямые проходящие через этот угол, продолжаясь, пересекают неограниченную прямую B. Пусть через точку K, через угол EKD проходит прямая MKL. Ещё раз напомню, что продолжаясь в сторону KM она никак не может пересечь неограниченную прямую B в силу девятой аксиомы (ей бы тогда пришлось во второй раз пересечь неограниченную прямую A). Значит если MKL и пересекает неограниченную прямую B, то только продолжаясь в сторону KL. Пусть прямая MKL пересекает прямую DK под углом DKL = β. Теперь если для прямой KL существует такая прямая KR которая пересекает прямую DK под углом DKR = α, причём β < α < ∟, и при этом, продолжаясь пересекает и неограниченную прямую B, то и KL, продолжаясь, тоже пересекает прямую B. Так пусть прямая KR, продолжаясь, пересекает неограниченную прямую B в точке O тогда рассмотрим треугольник ODK.

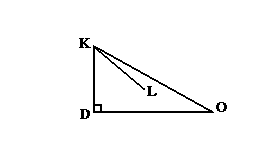
рисунок 48

Прямая же KL входит в его угол DKO и в силу девятой аксиомы, продолжаясь пересекает его сторону DO, то есть неограниченную прямую B, между точками D и O.

Докажем тогда, что для любой произвольно взятой прямой DKL проходящей через угол DKE под углом β к прямой DK (как показано на рисунке) (11) существует прямая KR, проходящая через этот угол под углом α > β и при этом не пераллельная неограниченной прямой B. Рассмотрим отдельно фигуру FDKE.

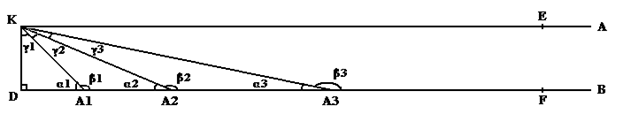
рисунок 49

И отложим на прямой DF DA1 = DK. Тогда ∆(DA1K) – равнобедренный и согласно пятому предложению Начал: < У равнобедренных треугольников углы при основании равны между собой, и по продолжении равных прямых углы под основанием будут равны между собой > (12) – угол γ1 = α1. Отложим теперь на прямой DF A1A2 = A1K рассмотрим ∆(A1A2K), в нём согласно пятому предложению Начал γ2 = α2. Кроме того, так как γ2 + α2 вместе с углом β1 составляют 2∟, и угол α1 вместе с углом β1 составляют 2∟, то α1 = γ2 + α2 и так как γ2 = α2, то α2 = α1 /2

То же самое касается и треугольника A2A3K (A2A3 = A2K): γ3 = α3, α3 = α2 /2, и всех остальных треугольников, которых можно построить сколь угодно много: ∆(DA1K), ∆(A1A2K), ∆(A2A3K), ∆(A3A4K) …… ∆(An-1AnK), а именно α2 = α1 /2, α3 = α2 /2, α4 = α3 /2, α5 = α4 /2 ….. αn = α(n-1) /2. Также мы знаем, что γ1 = α1, γ2 = α2, γ3 = α3, γ4 = α4 ….. γn = αn. Значит везде αi можно заменить на γi, значит γ2 = γ1 /2, γ3 = γ2 /2, γ4 = γ3 /2, γ5 = γ4 /2 ….. γn = γ(n-1) /2

А так как γ1 = ∟ /2 (13) далее для удобства примем прямой угол за единицу.

γ1 = ½, γ2 = ½ /2 = 1 /(2*2), γ3 = 1 /(2*2*2), γ4 = 1 /(2*2*2*2), γn = 1 /(2^n)

γ1 = ½, γ2 = 1/4, γ3 = 1/8, γ4 = 1/16, γ5 = 1/32, γ6 = 1/64, γ7 = 1/128

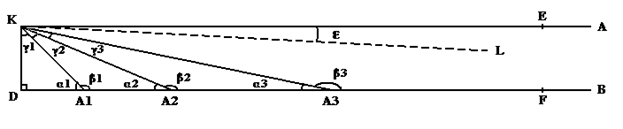
рисунок 51

Значит γn = 1 /(2^n)

Рассмотрим последовательность углов A1KE, A2KE, A3KE ….. AnKE, и будем их обозначать для краткости t1, t2, t3, …., tn

t1 = γ1 (так как t1 + γ1 = уголDKE = ∟, а γ1 = ∟ /2)

Поскольку теперь γ1 = t1, то γ2 будучи половиной γ1, является половиной и t1. Значит γ2 это половина t1. Будучи же половиной t1, γ2 равняется t2 (это видно из рисунка)

t2 = γ2.

Поскольку теперь γ2 = t2, то γ3 будучи половиной γ2, является половиной и t2. Значит γ3 это половина t2. Будучи же половиной t2, γ3 равняется t3.

t3 = γ3.

Подобным же образом можно доказать, что

t4 = γ4, t5 = γ5, t6 = γ6, t7 = γ7, ….., tn = γn

А так как γn = 1 /(2^n) то есть γ1 = ½, γ2 = ½ /2 = 1 /(2*2), γ3 = 1 /(2*2*2) и так далее

то tn = 1 /(2^n) Значит уголAnKE = 1 /(2^n)

Значит можно построить сколь угодно малый угол AnKE, то есть такой, что он будет меньше любого наперёд заданного угла.*
Значит для любой прямой KL, проходящей через угол DKE под углом ε к прямой KE (как показано на рисунке) существует точка An, (лежащая на неограниченной прямой B) такая, что прямая AnK проходит через угол DKE под углом AnKE меньшим чем ε и пересекает неограниченную прямую B в точке An. Значит и любая прямая KL проходящая через угол DKE пересекает неограниченную прямую B в силу девятой аксиомы.

То есть мы доказали, что для любой прямой KL проходящей через угол DKE (и через точку K) существует прямая, которая проходит через угол (DKE), под меньшим углом к прямой KE чем прямая KL и при этом пересекает неограниченную прямую B. Значит и прямая KL пересекает неограниченную прямую B. Значит через точку K не лежащую на неограниченной прямой B проходит только одна прямая (KE) параллельная данной. Таким образом мы доказали одиннадцатую аксиому из теоремы о сумме углов прямолинейного треугольника и теперь знаем, что из одиннадцатой аксиомы можно доказать эту теорему и обратно.

* То есть дробь 1 /(2^n) может принимать значения меньшие любой наперёд заданной величины. Это видно из того, что её знаменатель может принимать значения большие любой наперёд заданной величины - то есть для любого N существует n, такое что 2^n > N. (Так будем считать очевидным, что увеличивая любую величину (в том числе и 2) каждый раз в два раза можно за конечное число шагов превысить любую наперёд заданную величину.)

ЗАМЕЧАНИЯ К ДОКАЗАТЕЛЬСТВАМ

· Во первых, теперь мы доказали, что в геометрии Лобачевского сумма углов всякого треугольника меньше двух прямых углов. Это ясно из того, что если бы в геометрии Лобачевского сумма углов треугольника была бы равна двум прямым, то в ней можно было бы доказать и утверждение аналогичное одиннадцатой аксиоме, в то время как геометрия Лобачевского основывается на утверждении её (одиннадцатой аксиоме) противоположном. (14)

· Приведённое мною доказательство того, что сумма углов треугольника (и прямолинейного и треугольника Лобачевского – так как это теорема общей геометрии) не может быть больше двух прямых, а также доказательство одиннадцатой аксиомы из теоремы о сумме углов прямолинейного треугольника – взяты мною (с незначительными изменениями и дополнениями) с сайта: www.pm298.ru/lobachevski8.php страница 5 где ссылаются на А. М. Лежандра - его учебник «Начала геометрии»

· Надо заметить, что построение прямой BK (как на рисунке), выполняемое нами при доказательстве теоремы о сумме углов прямолинейного треугольника, всегда возможно. Так как угол β под которым она

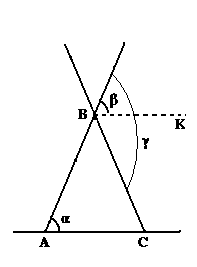
рисунок 52

строится, всегда меньше угла γ так как β = α, в то время как γ должен быть больше чем α так как прямые BC и AC пересекаются в точке С (то есть внешний угол γ должен быть больше - внутреннего α, а значит и γ > β так как β = α.)