Групповая скорость волн

7.1 Волновой пакет

Бесконечная гармоническая монохроматическая волна частоты 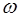, распространяющаяся в пространстве – это иде-ализация, необходимая для установления основных зако-номерностей. Помимо бесконечности в пространстве гар-моническая волна бесконечна во времени. Однако, беско-нечных волновых процессов в природе не происходит, вол-ны имеют начало и конец, и такие волны уже описываются другой функцией. Любая реальная волна может быть пред-ставлена как суперпозиция монохроматических волн с раз-личными амплитудами и частотами 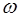в некотором интер-вале 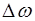. Поэтому любая волна имеет некоторую степень монохроматичности, ее частота имеет некоторый разброс 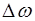около основной частоты 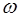. Суперпозицию волн, мало отличающихся друг от друга по частотам (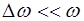) называют волновым пакетом или группой волн. (рис. 7.1).

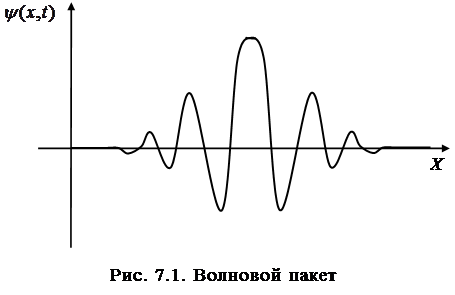В пределах волнового пакета волны усиливают друг друга, вне пакета – практически гасят друг друга.

Кроме того, гармоническая волна информации не пере-дает – ее n -й максимум (или минимум) ничем не отли-чается ни от n +1-го, ни от n –1-го. Для того, чтобы пере-дать информацию с помощью волны, ее надо модули-ровать – то есть изменять амплитуду, частоту или фазу волны. Для передачи сигнала и используется амплитуд-ная, частотная и фазовая модуляция.

Рассмотрим распространение волнового пакета на при-мере амплитудной модуляции.

Пусть в точке x =0 полубесконечной струны находится передатчик, который создает колебания, являющиеся су-перпозицией двух колебаний с разными частотам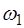и и :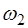

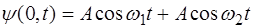. (7.1)

Преобразовав сумму косинусов согласно правилу (4.4), получим:

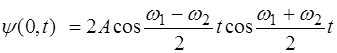. (7.2)

Полусумма частот образует среднюю частоту коле-баний:

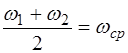, (7.3)

а полуразность – частоту модуляции:

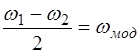. (7.4)

Таким образом, колебания (7.2) представляют собой колебания с переменной амплитудой 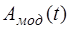, т.е. ампли-тудно-модулированные колебания, происходящие со сред-ней частотой:

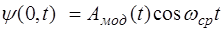. (7.5)

Амплитуда изменяется с частотой модуляции:

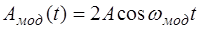. (7.6)

Передатчик, создающий амплитудно-модулированые ко-лебания, излучает по струне волну, бегущую в поло-жительном направлении оси X. Эта волна является супер-позицией двух волн с частотам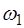и и :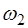

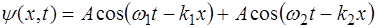. (7.7)

Применяя правило (4.4), получим:

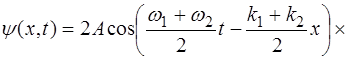
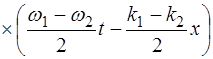. (7.8)

Введя обозначения для среднего волнового числа:

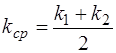, (7.9)

и волнового числа модуляции:

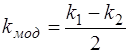, (7.10)

из (7.8) получим:

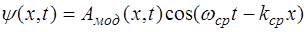, (7.11)

где

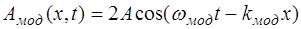. (7.12)

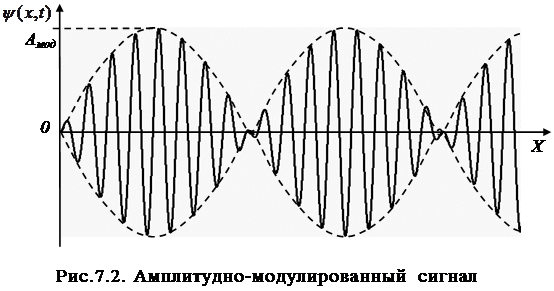
Уравнение (7.11) отражает распространение ампли-тудно-модулированного сигнала в виде серии волновых пакетов. На рис. 7.2 показан график такого сигнала в фиксированный момент времени.

7.2 Групповая скорость

Найдём скорость распространения максимума волново-го пакета, т.е. точки, в которой A_мод =2 A. Для этого зафик-сируем фазу волны распространения A_мод, описываемой уравнением (7.12):

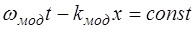. (7.13)

Продифференцировав (1.13) по времени, получим:

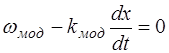, (7.14)

откуда получаем:

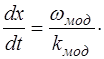(7.15)

Производная от координаты по времени и есть искомая скорость распространения волнового пакета, называемая групповой скоростью:

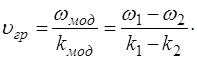(7.15)

Найдем более выражение для групповой скорости в диспергирующих средах. Пусть для такой среды задано дисперсионное отношение:

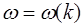. (7.16)

Тогда, разложив в ряд Тейлора и перенебрегая про-изводными высших порядков, запишем:

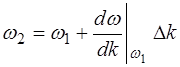. (7.17)

Учитывая, что 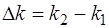, получим, учитывая (7.15), что групповая скорость волнового пакета равна:

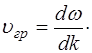(7.18)

В уравнении (7.11) есть еще одна составляющая, ко-торая описывает волну, распространяющуюся в положи-тельном направлении оси X. Зафиксировав фазу этой вол-ны:

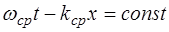, (7.19)

и проведя рассуждения, аналогичные тем, что мы прово-дили при определении групповой скорости, получим вы-ражение для фазовой скорости волны, составляющей вол-новой пакет:

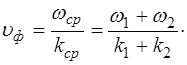(7.20)

Подведем итоги. Если есть диспергирующая среда, в ко-торой выполняется дисперсионное соотношение (7.16), то возникает понятие групповой скорости 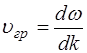, которая в общем случае отлична от фазовой .

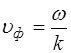В недиспергирующей среде групповая скорость оказы-вается равной фазовой, но возмущение не образуется, и передать информацию становится невозможным.

Date: 2015-07-27; view: 467; Нарушение авторских прав