Устойчивость системы при больших коэффициентах усиления

Передаточная функция для системы на рис. 6.2 имеет следующий вид:

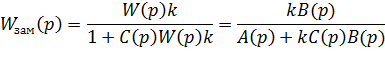
Запишем характеристическое уравнение этой системы.

Сделаем несколько предположений для уравнения (7.1).

Предположение 1: .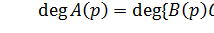

Тогда при k →∞ (k может быть как угодно большим) все коэффициенты А (р) будут мало заметны по сравнению с коэффициентами 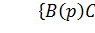Следовательно, можно коэффициентами А (р) пренебречь. Получим новое характеристическое уравнение:

Таким образом, имеем полную независимость свободных свойств системы от параметров объекта (его знаменателя А (р)). Это свойство было ожидаемым, так как было введено форсирующее звено.

Условие устойчивости нового характеристического уравнения (7.2) распадается на два условия: 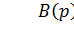и 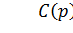. Для устойчивости системы с большим коэффициентом требуется устойчивость отдельно полинома В (р) и полинома С (р). Их корни должны быть левыми (с отрицательной вещественной частью). Так как полином С (р) конструируется нами, то он всегда устойчив. Полином В (р) берется из объекта. Следовательно, он может иметь правые корни. В таком случае числитель объекта себя проявит, и замкнутая система станет неустойчивой. Тогда система с большими коэффициентами будет неработоспособной.

Обычная система (без больших коэффициентов) может работать и при правых корнях числителя объекта.

Предположение 2: .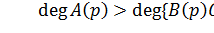

Имеем .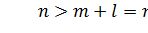

Допустим, сэкономили и порядок l выбрали не (n-m), а меньше.

Тогда, пренебрегая членами А (р), получим новое характеристическое уравнение

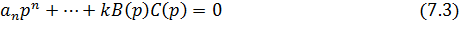
Уравнение (7.3) имеет порядок n. В таком случае, если зависит от t, то невозможно компенсировать переменные параметры. Если порядок С (р) будет ещё ниже, то большее количество коэффициентов полинома А (р) будут проявляться в динамике системы.

Рассмотрим свойства полинома (7.3) на высоких частотах (р →∞). Тогда в полиноме (7.3) останутся только старшие коэффициенты.

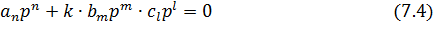
Пусть 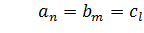Уравнение (7.4) распадается на два уравнение (выносятся нулевые корни):

Из уравнения (7.5) имеем корни p ₁=0 кратности (n-1) и р ₂= - k. Как видим, на высоких частотах преобладает один корень р ₂= - k. Таким образом, эта система всегда устойчива (так как k >0) и работоспособна.

Рассмотрим случай, когда порядок C (p) ниже на 1. Следовательно, получим уравнение второго порядка (в нем нет демпфирования, так как система с большим коэффициентом) .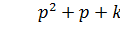

Вывод: Если 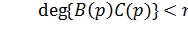, то есть 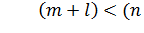, то система неработоспособна при больших коэффициентах.

Иначе: Чтобы система была устойчива необходимо ввести инерционность С (р) такого порядка, чтобы порядок 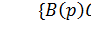был не ниже (n -1).

Date: 2015-07-27; view: 464; Нарушение авторских прав