Наибольшее и наименьшее значения функции двух переменных в замкнутой области (глобальный экстремум)

Правило нахождения наибольшего и наименьшего значений дифференцируемой

в области D функции z= f(х; у) состоит в следующем:

1. Найти все критические точки функции, принадлежащие D, и

вычислить значения функции в них;

2. Найти наибольшее и наименьшее значения функции z = f(x;y)

на границах области;

3. Сравнить все найденные значения функции и выбрать из них

наибольшее M и наименьшее m.

21. Основные методы вычисления определенного интеграла.

Формула-Ньютона –Лейбница.

Если F(x) – одна из первообразных непрерывной на [a;b] функция 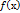, то справедлива следующая формула 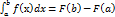(1)

Замена переменной (подстановка) в определенном интеграле.

Если функция 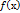непрерывна на [a;b], а функция х=φ(t) непрерывна дифференцируема на [t1;t2], причем φ([t1;t2])= [a;b], то справедлива формула 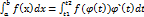(2) – формула замены переменных в определенном интеграле. φ(t1)=a φ(t2)=b.

Интегрирование по частям в определенном интеграле.

Пусть u(x) и v(x) дифференцируемые на отрезке [a;b] функция переменой х, тогда дифференциал d(u;v)=udv+vdu. Проинтегрируем обе части данного равенства на [a;b] 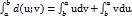(3) По формуле Ньютона-Лейбница 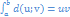следовательно (3) имеет вид 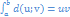(4) Формула (4) называется формулой интегрирования по частям в определенном интеграле.

22.Несобственные интегралы с бесконечнымиверхними пределами (первого рода).

Пусть функция f(x) непрерывна при а ≤х<+∞,также пусть функция интегрируема на любом конечном отрезке [а;А], А>а. Тогда на отрезке [а;А] существует определенный интеграл Римана. Этот определенный интеграл является функцией верхнего предела А: F(x)= 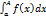. Рассмотрим предел функции F(A) при А стремящемся к +∞:

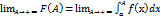(1)

Предел (1), если он существует называется несобственным интегралом первого рода от функции f(x) на полупрямой [а;+∞] и обозначается 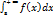(2).

При этом говорят, что (2) сходится и интеграл = .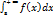

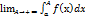Если предел (1) не существует, то говорят, что несобственный интеграл (2) расходится.

Геометрически для неотрицательной при х≥а функции f(x) несобственный интеграл (2) представляет собой площадь фигуры ограниченной сверху графиком функции у= f(x), слева отрезком прямой х=а, снизу осью Ох.

Аналогично определяется и несобственный интеграл 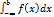для функции f(x) определённый на полупрямой х≤и и интегрируемый по Риману [В;b]

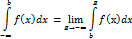
Несобственный интеграл с двумя бесконечными пределами интегрируя от непрерывной функции f(x) на интервале ]-∞;∞[ предварительно представим в виде 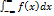= 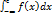+ 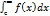,с€]-∞;∞[. Тогда по определению + 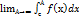(3).Причем этот интеграл называется сходящимся, если оба предела существуют. Если хотя бы один из пределов не существует или бесконечен, то (3) называется расходящимся.

Теорема 1

Пусть на полупрямой а ≤х<+∞ выполняется неравенство /f(x)/≤g(x). Тогда из сходимости интегралов .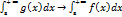

Теорема 2

Пусть функция f(x) является ограниченной по сравнению с функцией g(x) при х стремящемся к +∞.Тогда если 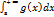сходится, то сходится и 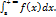А если первый расходится, то и второй расходится.

23. Несобственные интегралы от неограниченных функций (второго рода).

Пусть функция f(x) определена на промежутке [a;b] и не ограничена в левосторонней окрестности точки. Т.е. .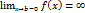

Будем считать, что функция f(x) интегрируема на отрезке [a;b-ɛ].Т.е. существует 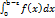зависящий от переменного верхнего предела интегрирования.

Несобственный интеграл от функции f(x) непрерывный на отрезке [a;b[ и имеющий бесконечный разрыв в точке х=и(несобственный интеграл второго рода) называется

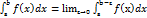(1)

Аналогично, если функция f(x) имеет бесконечный разрыв в точке х=а, то полагают 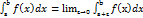(2)

Если же функция f(x) имеет разрыв второго рода, в которой внутренняя точка С определена промежутке [a;b],то данный интеграл можно представить в виде суммы двух интегралов: 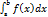= = 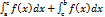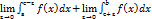(3)

Если пределы в правых частях формул (1),(2),(3) существуют и конечны,то соответственно неопределенный интегралы от разрывной функции в точках а,в,с называются сходящимися. В противном случае – расходящимися.

С геометрической точке зрения сходящийся несобственный интеграл второго рода означает, что фигура ограниченная кривой у= f(x),прямыми х=а и х=в и бесконечно вытянутая в направлении оси Оу, при х стремящемся к в-0 имеет конечную плоскость S.

24. Геометрические приложения определенного интеграла. Вычисление площадей плоских фигур в прямоугольной и полярной системах координат

Из геометрического смысла определенного интеграла следует, что если f(x)≥0, то площадь криволинейной трапеции, ограниченной кривой у= f(x) осью Ох и прямыми х=а и х=b, может быть вычислена по формулам S= 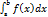= 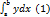, S≥0.

Если f(x)<0, то 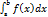<0, если а<b.Следовательно в этом случае S= 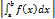= 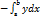. Если криволинейная трапеция ограничена кривой х=z(y) осью ординат Оу и прямыми у=с и у=d, то ее площадь определяется формулой S= 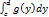= 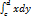.(2)

Если подынтегральная функция f(x) конечное число раз меняет знак на отрезке [a;b], то интеграл (1) равен алгебраической сумме площадей соответствующих криволинейных трапеций, лежащих под осью Ох(+) и под этой осью (-).

Для того чтобы получить общую площадь данной фигуры отрезок интегрирования нужно разбить на частные отрезки, на которых функция 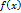сохраняет знак и применить формулы (1) (2),тогда S= .

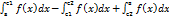Площадь плоской фигуры ограниченной прямыми х=а и х=и и двумя непрерывными кривыми у= f1(x) и у= f2(x) (f1(x) ≤ f2(x),вычисляется по формуле S= .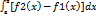

Если фигура ограничена прямыми у=с и у=в и кривыми х= g1(y) и x= g2(y), то ее площадь определяется формулой S= .(g1(y)≤ g2(y))

Если криволинейная трапеция ограничена линиями заданными в параметрической форме: х=х(t) y=y(t) t1≤t≤t2 осью Ох и прямыми х=а и х=и причем х(t1)=а и х(t2)=b, то ее площадь находится по формуле S=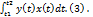

Площадь криволинейного сектора одной прямой заданной в полярных координатах уравнением r=r(φ) и двумя полярными радиусами φ1=α и φ2=β(α<β) выражается S= .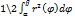

Если фигура ограничена двумя полярными радиусами φ=α и φ=β и кривыми r=r1(φ)и r=r2(φ), где r1(φ)≤ r2(φ), то ее площадь находится по формуле S= .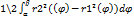

25. Геометрические приложения определенного интеграла. Вычисление длины дуги плоской кривой.

Пусть функция у= f(x) определена и непрерывна на отрезке [a;b], и кривая L- график этой функции. Требуется найти длину дуги плоской кривой, ограниченную прямыми х=а и х=b.

Разобьем отрезок [a;b] произвольным образом на n частей точками а=х0<х1<х2…<хn= с.

Обозначим Δхi=xi-xi-1, i=1,n.

Через точки xi проведем вертикальные прямые параллельные оси Оу до пересечения с кривой L. Тогда дуга аb разобьется на n частей. Соединив каждые две соседние точки разбиения кривой L отрезками, получим ломанную АМ1М2…Мn-1В вписанную дугу АВ.

Обозначим длину ломанной Ln= ΙАМ1Ι+ΙМ1М2Ι+…+ΙМn-1ВΙ= 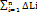, где 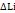-длина хорды стягивающей дугу. Длина ломанной является приближенным значением длины дуги АВ.

Если увеличивать число точек разбиения отрезка [a;b] на частные отрезки так, чтобы длина max из них стремилась к 0, то длина вписанной ломанной стремится к длине дуги прямой АВ.

Если существует конечный предел Lnпри λ стремящейся к 0, λ= maxΔхi, то этот предел принимается за длину дуги L основную дугу называют спрямляющейL 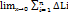(1)

Если конечный предел Ln не существует, то и длина дуги не существует, а сама дуга называется не спрямляемой. Длина стягивающей хорды L= 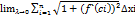(2).

В правой части (2) стоит интегрированная сумма для функции 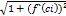на отрезке [a;b]. Предел такой суммы существует и равен определенному интегралу от этой функции на [a;b] L= . Если уравнение кривой задано параметрически х=х(t) y=y(t) t€[ t1t2],то для нахождения длины дуги плоской фигуры воспользуемся (3) выполнив замену переменных х=x(t), dx=x`(t)dt, y`(x)=y`(t)\x`(t), L= (4). В полярной системе координат r=r(φ) предположим, что r(φ) и r`(φ) непрерывны на [α<β]. Эту кривую можно задать параметрически, т. к. между полярными и декртовой системамисуществует следующая зависимость 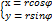Т.к. 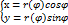φ€[α<β].

Эти уравнения можно рассматривать как параметрические уравнения кривой и для вычисления длины дуги можно применить формулу (4) ,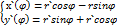

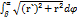( ²=(r`)²+r², L= (5).

26.Геометрические приложения определенного интеграла. Вычисление объёмов тел по площадям его параллельных сечений. Объём тела вращения

Если площадь сечения тела S плоскостью перпендикулярной оси Охявляется непрерывной функцией на отрезке [a;b], то объем части тела заключенной между плоскостями х=а, х=и параллельные к оси Ох находятся по формуле V= 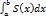, т.е.при изменении х на величину dx дифференциал объема тела равен объему прямого цилиндра с высотой dx и площадью основания 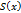. Если криволинейная трапеция ограниченная кривой y=f(x) и прямыми у=0 и х=а и х=b вращается вокруг оси Ох, то объем тела вращения вычисляется по формуле: V= 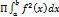. Если фигура ограничена прямыми х=а и х=b и кривыми у=f1(x) и у= f2(x), то объем тела вращения находится по формуле V=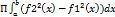

27.Физические приложения определенного интеграла.

Статистическим моментом материальной точки находящейся в плоскости Оху, относительно координатной о си Ох лил Оу, называется произведение массы этой точки на ее ординату (абсциссу).

Статистическим моментом системы таких точек относительно координатныхосей называется сумма статических моментов всех точек относительно этой оси.

Центром тяжести (центром масс)системы материальных точек называется точка Мс(Хс;Ус) плоскости, обладающая тем свойством, что если в Мс сосредоточить всю массу системы m=m1+..mn, то ее статический момент по отношению к любой оси равен статическому моменту системы точек относительно той же оси.

Если обозначить через и 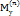статистические моменты системы точек относительно осей Ох и Оу, то координаты центра тяжести удовлетворяют соотношению

mXc= 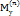=m1X1+…mnXn

mYc= = m1Y1+…mnYn

Следовательно центр тяжести данной системы материальных точек имеет координаты

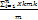Xc= Yc= 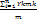. Статистические моменты и координаты центра тяжести дуги плоской линии можно выразить через определенный интеграл.

Пусть дуга АВ задана уравнением y=f(x),где f(x) – дифференцируемая функция на отрезке [a;b], И на этой дуге распределено вещество с плотностью р=р(х). Разделим дугу АВ на n частных дуг в одной ее точке. Тогда получим приближенное выражение элемента массы Δmk=p(Хк)(Мк-1Мк).Элементы статических мометов относительно координтных осей (ΔМх)к=УкΔmk, (ΔМy)к=XкΔmkСуммируя и переходя к пределу, λ стремится к 0, получим выражение массы материальной дуги m= 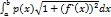и ее статистических моментов относительно координатных осей Мх= 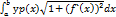и Му= 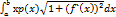. Для нахождения центра тяжести материальной дуги в соответствии с определением составим равенство mXc=My, mYc=Mx. Xc=My\m, Yc=Mx\m

Момент инерции материальной кривой АВ с линейной плотностью р(х), заданной уравнением y=f(x) имеющей непрерывную производную y`=f`(x) на [a;b] относительно начала координат вычисляется по формуле Jo= 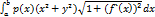, при этом

Jх= 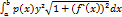и Jу= 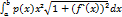– моменты инерции кривой относительно осей Ох и Оу соответственно и Jo= Jх₊Jу.

30. Криволинейные координаты на плоскости. Якобиан. Замена переменных в двойном интеграле

Криволинейные координаты на плоскости.

Рассмотрим непрерывно дифференцируемые функцииu иvв прямоугольной декартовой системе координат (х;у)

u=φ(x;у) и v=ᴪ(x;у) (1). Предположим, что ур. (1) однозначно разрешимы относительно х и у: х=φ1(u;v) и у=ᴪ1(u;v) (2). Передавая поочередно uv различные возможные для них постоянные значения,получаем два семейства линий на плоскости. Эти линии называют координатными линиями.Положение точки М на плоскости определяется парой чисел x;у или парой чисел u;v. Числа u;v – криволинейные координаты точки М на плоскости. Примером криволинейных координат являются полярные координаты(координатные линии – концентрические окружности и полу кривые исходящие из начала координат). Также частным случаем криволинейных координат являются прямоугольные координаты(координатные линии – прямые параллельные осям координат)

Если непрерывно дифференцируемые функции (2) осуществляют взаимно-однозначное отображение области Д на область G, то

(3)

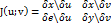(4)– функциональный определитель (ЯКОБИАН)

Рассмотрим частный случай замены переменных часто используемый при вычислении двойного интеграла:замену декартовых координат полярными, которые связаны с декартовыми соотношениями x=rcosφ и у=rsinφ

Правые части этих равенств непрерывно-дифференцируемые функции. Якобиан преобразования определяется из (4) J(r;φ)= 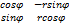=г

Формула замены переменных (3) принимает вид (5). Для вычисления двойного интеграла в полярных координатах тоже правило сведения его к повторному интегралу.

28. Определение двойного интеграла и его свойства, Физический и геометрический смысл двойного интеграла.

Двойной интеграл представляет собой обобщение понятий определенного интеграла на двумерный случай. Вместо функции одной переменной y=f(x) будем рассматривать функцию двух переменных z=f(x;у) определенную на некоторой ограниченной области Д декартовой плоскости Оху.

Потребуем, чтобы область Д обладала конечной плоскостью. Замыканием 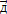области Д назовем объединение области и ее границы

Будем считать, что для всех точек из Д определена и непрерывна функция f(у). Рассмотрим разбиение области Д на подобласти Д1,Д2,Д3…Дn удовлетворяющие следующим условиям 1)объединение подобластей Дi полностью покрывет область Д.2)подобласти Дi могут пересекаться только по своим граничным точкам 3) определены площади подобластей Дi

Определим диаметр множества Дi как наибольшее из расстояний между двумя точками множества Дi след. Образом d(Дi)=supp(M;N) (sup-наивысший)

Диаметр dt всего разбиения назов. Наибольшее из чисел d(Дi), dt=maxd(Дi)

Выберем в каждой части (Дi), произвольным образом точку pi(ϝi;Ϟi) и составим сумму St= 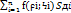(1), которую назовем интегральной суммой для функции f(x;у) в области Д.

Если существует предел интегральный сумме (1) при стремлении к 0 диаметра разбиения dt, причем он не зависит не от выбора разбиений не от выбора точек pi в областях Дi, то такой предел называется двойным интегралом от функции f(x;у) до области Д: (2)

Кривая называется гладкой если к каждой ее точке существует касательная и при переходе от точки к точке положение этой касательной меняется непрерывно. Непрерывная прямая составленная из конечного числа гладких прямых называется кусочно-гладкой.

Теорема 1(о существовании и единственности двойного интеграла)

Если область Д с кусочно-гладкой кривой ограничена и замкнута, а функция f(x;у) непрерывна в области Д,то эта функция интегрируема в области Д.

Геометрический смысл двойного интеграла-в случае не отрицательной функции f(x;у) двойной интеграл по области Д представляет собой объем криволинейного цилиндра построенного на области Д и ограниченного сверху поверхностью z= f(x;у)

Свойства

1)свойство линейности

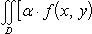
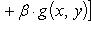
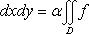
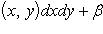
2) свойство аддитивности

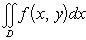
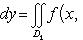
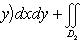
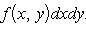
3)Знак интеграла совпадает со знаком функции

4)Двойной интеграл от еденичной функции по области Дчисленно равен площади интегрирования Sд=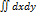

.5)Теорема о среднем

Если обе функции f(x, y) и g(x, y) интегрируемы в области D, функция g(x, y) неотрицательна (неположительна) всюду в этой области, M и m - точная верхняя и точная нижняя грани функции f(x, y) в области D, то найдется число μ, удовлетворяющее неравенству m ≤ μ ≤ M и такое, что справедлива формула

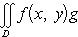
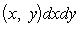
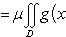
29.Вычисление двойных интегралов в декартовой системе координат. Перемена порядка интегрирования в повторном интеграле.

Рассмотрим на плоскости Оху область Д ограниченную прямыми х=а и х=b и кривыми у=φ1(х) и у=φ2(х), где φ1 и φ2 непрерывны на отрезке 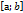причем φ1(х)≤ φ2(х). Такую область будем называть правильной областью первого типа.

Пусть также задана f(x;y) непрерывная по Д. Для любого фиксированного значения х€ 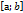можно определить функцию F(x)= 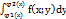. Функция F(x) непрерывна и следовательно интегрируема на отрезке 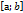.Назовем повторным интегралом значение определенного интеграла от F(x) на отрезке 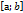Iд= 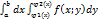(1).Аналогично может быть рассмотрена область Д`, ограниченная прямыми у=с и у=d и кривыми х=ᴪ1(у) и х=ᴪ2(у). Функции ᴪ1 и ᴪ2 непрерывны на отрезке [с;d] причем ᴪ1(у)≤ ᴪ2(у). Такая область называется правильной областью второго типа.

Для непрерывной функции f(x;y) можно определить повторный интеграл аналогично (1), но с другим порядком интегрирования Iд`= 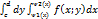(2)

Теорема 1

Пусть правильная область Д(первого типа) ограничена линиями х=а и х= b у=f1(x) и у= f2(x), где функции f1 и f2 непрерывны на отрезке 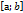, а функция f(x;y) непрерывна на замыкании 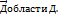Тогда двойной интеграл от этой функции совпадает по области Д с повторным 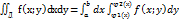(3), аналогично для правильной области второго типа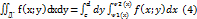

15.Многочлены и рациональные функции. Теорема Безу. Основная теорема алгебры.

Остаток от дел. Мн-на(х-а)---знач этого мн-на при х=а.

Следствие(безу) Мн-н Р(х) дел без остатка наь (х-а) только в том случ, когда а есть его корень.

Основные теоремы Алгебры:Всякий множ отличн от постоян имЕЕТ по крайне мере один корень. Из осн теоремы алгебры и т-мы Безу след, что всякий многочлен степени п разл по п-лин. Множителей…т.к. Р(х) имеет нек.корень а1=(х-а1)Р₁(х), где Р₁(х) многочлен степени п-1.Р₁(х) имеент нек. Корень а1, кот дел на а2 поэтому:Р (х)=(х-а1)(х-а2)Р₂(х), Р₂(х)=п-2..продолжая рассуждл получим:Р (х)=А(х-а1)(х-а2)…(х-ап), А-степ коэф многочлена В(х), т.к. разложен един, то мн-н п-степени имеет не более п-корнней.

Корень кратности 1 наз простым, 2-двойным,0-не явл корнем.из сказ след что всякий множ имеет ровно п-корней, если кажд корень считать столько раз какова его кратность.

Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид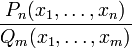

где 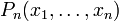, 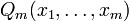— многочлены от любого числа переменных.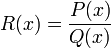

Частным случаем являются рациональные функции одного переменного:

, где P(x) и Q(x) — многочлены.

Функция называется рациональной функцией, или рациональной дробью, если она представляет собой отношение двух многочленов и:

Пусть степень многочлена равна, а степень равна, то есть где и. Разделив числитель и знаменатель на число, мы получим, что коэффициент при старшей степени в знаменателе равен 1. Для дальнейшего нам будет удобно предполагать, что эта операция уже произведена, то есть что. Далее мы будем предполагать, что все коэффициенты и -- вещественные числа.

Если, то дробь называется правильной, а если, то неправильной. Если дробь неправильная, то её числитель можно поделить на знаменатель, получив при этом частное и остаток, степень которого меньше. Это означает, что

или что где -- некоторый многочлен, называемый целой частью рациональной дроби. Если остаток тождественно равен 0, то многочлен делится на без остатка, и функция является многочленом, то есть совпадает со своей целой частью.С интегрированием целой части дроби, то есть многочлена, не возникает никаких проблем, так что в дальнейшем мы можем заняться выяснением способов интегрирования лишь правильных рациональных

дробей.

11.Условный экстремум ФНП (метод множителей Лагранжа). Метод наименьших квадратов.

.функция и=F(M)=f(x1,x2…xn) иммет усл. Миним(максим) в т М₀(x₁^0/…x_n⁰) если сущ такая окр. точки М₀длоя всех т М которой М не = М₀ удовлет ур-я связи 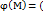x1,x2…xn.)=0 задача нахожд усл.экстр свод к исслед. Нам обычн. Экспер ф.Лагранжа:

\

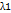- множитенль лагранжа.

:если 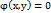то ф-ла лагранжа имеет вид L(x,y, 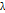)=F(x,y)+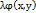

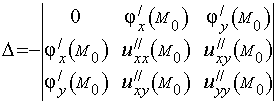
Если определитель, то M0 есть точка условного минимума, если, то M0 – точка условного максимума.

МНК:

Пусть проведено н-экстрем по измер 2-ух велич. Х и У в рез. Кот получ значение (х1……хn)(y1….yn)При анализе зависим перем у(х) установл, что неиз ф-ции завис y=F(x) можно опис с пом. Многочлена:

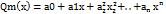
Для оценки близ.f(x) и Q(x) ввод величину:

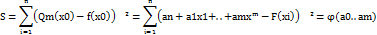
Кот явл ф-цией m+1 пер.коэф..Если эти коэф выбрать так, чтобы ф. S была миним., то наша задача будет решена.Величина Qm(xi)-F(xi) –отклонение.Для определения а0…ат необх усл экстремума: 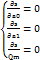введем обозначения:S_k=x₁^k+..+ x_n^k иt_k=x₁^ky₁+..+x_n^xy_n

Тогда можно преобр:

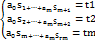
Пусть а1=а0+а1х, тогда ,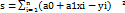

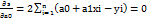, cистему можно записать в виде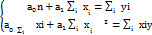

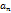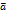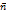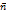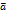48. Потоком векторного поля через поверхность S в сторону определенную единичным вектором нормали к поверхности S называют интеграл: где -проекция вектора на направление нормали . dS-(элемент площади поверхности)диференциал. В декальтовой системе коорд.,если имеет координаты cosα,cosβ,cosγ, то . Поток вектора – скалярная величина. Величина потока равна объему жидкости, который протекает поверхность S за единицу времени(физический смысл потока). Если поверхность замкнута и ограничивает некоторый объем V, то поток вектора записывается в виде: 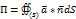В этом случае за направление вектора n берут направление внешней нормали и говорят о потоке внутри поверхности S. Диввергенцией (расходимостью ) векторного поля a(M) в точке М области V называется 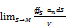если он существует. Теорема. Если функции P,Q,R непрерывные вместе со своими частными производными в области V,то дивергенция поля a существует во всех точках области V и в любой декальтовой системе координат выражается формулой: 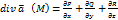Некоторые свойства дивенгерции: 1)Если 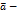const, то div 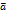=0 2)div(c- 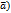=cdiv

.

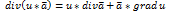
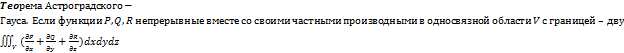Эта формула носит название формулы Астроградского-Гауса и выражает следующий результат: поток векторного поля через замкнутую поверхность в направлении к внешней нормали к ней равен тройному интегралу от дивергенции этого поля, взятой по области, ограниченной этой поверхностью

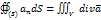dV.

47.Скалярные и векторные поля. Скалярные. По лем называется область пространства, в каждой точке которой определено значение нек. величины. Если в каждой точке М области соответствует определенное число u=u(M), то говорят, что в области определено(задано) скалярное поле или функция точки. Если функция U(M) зависит от времени, то скалярное поле называется стационарным.пример:u=u(x,y,z,τ). Поле, которое меняется с течением времени, называется нестационарным. Обычно предполагается, что функция поля непрерывна и имеет непрерывные частные производные. Графически скалярное поле можно изобразить с помощью пов-ти уровня,где С-const, f(x,y,z)=C. Или если скалярное поле плоское f(x,y)=C. Производной скалярного поля в точке М по направлению вектора L называется предел,если он существует, отношением прирощением 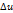функции u(M) при смещении точки М в направлении вектора L к величине этого смещения d=(M 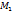), когда d 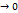. МLM

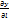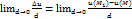= Еслиx,y,z- координаты фиксированной точки М; cosα,cosβ,cosγ- направляющие cos 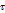, то 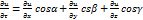Подобно тому,как частные производные 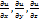характеризуют скорость изменения функции U в направлении осей координат, так и производная по направлению 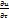будет являться скороcтью изменения функции U в точке М по направлению L.

ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ ПО НАПРАВЛЕНИЮ. Абсолютная величина производной по напрвлениюL определяет величину скорости, а знак производной характеризует изменения функции U.

Вектор с координатами 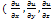) направлен по нормали поверхности уровня и называется градиентом скалярного поля. Обозначим через 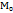(cosα,cosβ,cosγ) единичный вектор направления L. Тогда 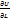– угол между векторами gradu и L. Т.е. производная скалярного поля U(M) в точке М в данном направлении равна проекции градиента поля в точке М на этом направлении. Отсюда следует, что 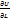в точке М имеет наибольшее значение в направлении gradиента.ФИЗИЧЕСКИЙ СМЫСЛ ГРАДИЕНТА. 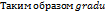– есть вектор,указывающий направление наибольшего возрастания скалярного поля в данной точке и имеющий модуль равный скорости этого возрастания. Векторные. Пусть В – область в пространстве.Если каждой точке М(x,y,z) из В сопоставлен вектор 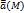, то говорят, что в области В задано векторное поле . Векторное поле, координаты которого не зависят от времени называется установившимся или стационарным. В прямоугольной системе координат Оxyz векторное поле записывается следующим образом: . P,Q,R – проекции вектора, заданного в точке М соответственно на коорд. OxOyOz. Предположим, что функции P,Q,R непрерывны вместе со своими частными производными. Векторное поле называется однородным если – постоянный вектор, т.е. P,Q и R постоянные величины. Векторное поле называется плоским, если проекция вектора не зависит от одной из трех переменных x,y,z и одна из проекций равна нулю. 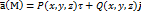Важной характеристикой стационарного векторного поля является семейство векторных полей, в каждой точке которых касательная направлена по вектору поля. Семейство векторных линий поля определяется системой дифференциальных уравнений: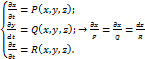

Векторные линии поля называют также силовыми линиями или линиями тока. Часть пространства, в которой задано векторное поле а(М),ограниченное некоторой поверхностью S, называется векторной трубкой. Векторная трубка- это часть пространства, состоящая из целых векторных линий,каждая из которых или целиком лежит в векторной трубке или целиком вне её.

49.циркуляция и ротор векторного

поля

Пусть векторное поле образовано вектором ā=P(x,y,z)ī + Q(x,y,z)j̄ +R(x,y,z)k̄. Возьмем в этом поле некоторую замкнутую кривую L и выберем на ней определенное направление. Пусть R=xī+yī+zk̄ радиус вектор в точке М на поле…известно, что dr̄=dxi+dyj+dzk, направлен по касательной кривой и │dr̄│=dl,где dl дифференциал дуги кривой. dl = корень из √ (dx)²+ (dy)²+ (dz)².

Криволинейный интеграл по замкнутому контуру L от скалярного произведения а̄ на dr̄касат. контуру L называется циркуляцией, а вдоль L: С=∫ᾱ*dr̄(1),Т.к. ᾱ*dr̄=│dr̄│* пр_L=α_r*dl=Pdx+Qdy+Rdz,где α_r–проекция ᾱ на касат. R. То равенство (1) можно записать в виде

С=∫ᾱ*dl(2) илиС=∫Pdx+Qdy+Rdz(3)

Циркуляция записанная в виде …имеет простой физический смысл, если крив.L расположена в силовом поле, то цирк. Это работа силы поля при перемещении точки до L вдоль рамки векторных линий цирк. Отлична от 0 пот. В каждой точке векторные линии скалярное произведение ᾱ*dr̄ сохраняет знак.полож.если направление ᾱ совпадает с направлением обхода вект.линии отриц. В противоположной точке.

Ротором или вихрем вект.поляā(М)= Р(x,y,z)ī+ Q(x,y,z)j̄+R(x,y,z)k̄на вектор обозначаемый rotā(M) и определяется формулой 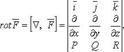.некоторые свойства ротора:

1.если ā пост.вектор, то rotā=0

2. rot(с*ā)=с* rotā (с-константа)

3. rot (а+в)= rota+ rotв

4.если U скалярная функция, а ā(М)-векторная., то rot(U*ā(U))=U* rotā+gradU 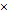ā

50.формула стокса

Теорема:

Если функции Р(x,y,z), Q(x,y,z), R(x,y,z) непрерывны вместе со своими частными производными 1-го порядка в точках ориентированных пов. ∫, то имеет место формула:

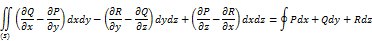
L-граница пов. ∫ и интегриров. Вдоль кривой Lпроизвод. В полож.напр.т.е. при обходе Lпов. Интеграла должна оставаться все время слева.

Доказательство

Пусть t=f(x,y), f(x,y), f’_x(x,y), f’_y(x,y) непрерывны в замкнутой обл. Д проекции поверхности ∫ на плоскость Оху, L₁ граница обл. Д.

Будем считать, что поверхностный интеграл пересекается с любой прямой параллельной оси Oz не более чем в 1 точке. Выберем верхнюю сторону пов. Интеграла. Рассмотрим сначала 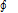Р(x,y,z) dx значение функции Р(x,y,z) L на L= значению функции Р(x,y,z(х,у)) на L_1.интегрирование суммы для криволинейного интеграла 2-го родаL₁ и L совпадают. Поэтому 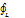Р(x,y,z) dx= 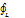Р(x,y,z(х,у)) dx, применяем к этому интегралу формулу градского, получим

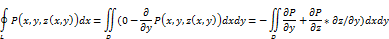
Преобразим полученный двойной интеграл в поверхностный интеграл 2-го рода.для этого последнее равенство перепишем в виде:

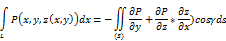
И используем уравнение нормали ∫, т.к. выбрана верхняя сторона ∫, т.е. cosᴕ>0 (ᴕуголмежду нормалью пов. ∫ и осью Oz), то нормаль N имеет проекции - ,- ,1

Направляющие cosпропорц. Cosβcosαcosᴕ=- ,- ,1

Отсюда 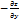, тогда - 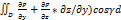S= , следовательно

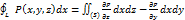
Аналогично получается при соответствующих условиях еще 2 равенства

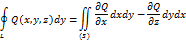
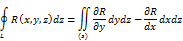
Складывая,почленно 3 последовательно равенства получим формулу стокса. Правая часть формулы представляет собой циркуляцию ᾱ по контуру L

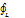Pdx+Qdy+Rdz= 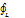α_r*dl.

Интеграл в левой части представляет собой поток вектора ротор ᾱ, через поверхность S ограниченную контуром 2? Следовательно формулу стокса можно записать в виде

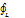α_r*dl=∫∫ rotā*dS

51. Простейшие векторные поля и их свойства

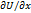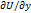Векторное поле а(М) наз. Потенциальным, если оно является градиентом некоторого скалярного поля, т.е. а̄(М)= grad а̄(М). В случае, если поле а̄ потенциально выполняется равенство Р= , Q= , R= 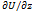это эквивалентно тому. что выражение Pdx+Qdy+Rdz=du является полным дифференциалом некоторой функции u. Эта функция называется потенциальным вектором поля а(М). векторное поле а̄(М) потенц. Обл. u тогда и только тогда когда rota(М)=о

Основные свойства потенциального поля

1.циркуляция потенциального поля по любому замкнутому контуру в этом поле=0

2.в потенциальном поле а криволин.∫

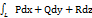вдоль любой кривой L с началом в М₁и концом в М₂ и зависит от положения т. М₁ и М₂ и не зависит от формулы кривой.

3. поле является полем некоторой функции U, т.е. если rota=0, то существует U(x,y,z):a=gradU

Замечание: из равенства rotgradU=0, обратное утверждение-поле град. Скал. ФункциUявлпотенц. Поле опред. Заданием 1 скал. Функции Uего потенциалом. Потенциал может быть найден:

U(x,y,z)=

Где x₀y₀z₀—координаты фиксированной точки,xyz—коорд. произв. точки.

52.Операторы Лапласа и Гамильтона. Операции второго порядка в векторном анализе

Основными дифференцированными операциями над скалярными полями U и в поля,явлgradU, rot и дивиргенцией, назвнут. Операцией 1-го порядка.эти операции удобно записывать с помощью оператора гамильтона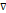

Этот символический вектор наз. Также оператором Набла.онпреобретает смысл лишь

Применяя оператор Набла получим диф.опертаор 1—го порядка

1. =gradU

2.

3.

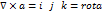
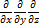
PQR

После применения оператора гамильтона скалярному или к векторному полю получим новое поле, к которому снова можно применить этот оператор. В результате получим дифферен.оператор 2-го порядка

1. dV(gradU)= +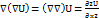

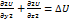
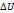Наз оператор лапласа скалярной функции Uи обозначается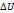

2. Rot(gradU)= 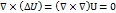,т.к.векторное произведение 2-ух одинаковых векторов=0 это означает, что поле градиента безвихревое

3. gradU(divā)=

4. div(rotā)= 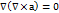, т.к. смешанное произведение 3-ех вект. Из которых 2 одинаковых=0

5. rot(rotā)= - векторная величина полученная в результате применения операт. Лапласа век.ст

Date: 2015-07-27; view: 1061; Нарушение авторских прав