Далее рассмотрим примеры

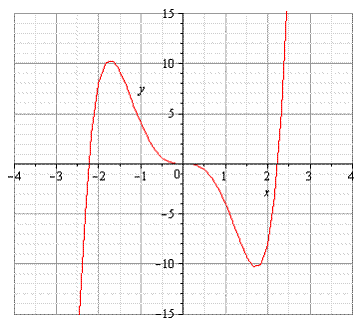
Пример 2.1. Исследовать функцию 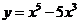и построить её график

1. Данная функция есть многочлен пятой степени. Область определения D многочлена интервал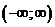

2. Определим нули функции. В данном случае это возможно

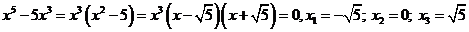
3. Функция нечётная, так как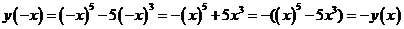

4. Определим участки монотонности и локальные экстремумы. Вычислим критические точки функции. У многочлена у всех критических точек 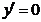. Отсюда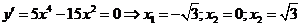

Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

Производная 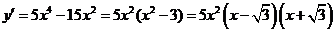положительна

на интервалах 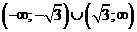. Производная отрицательна на интервалах

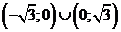. Вычисляем значения функции в критических точках

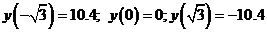и заполняем таблицу.

x		-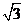
	+		-		-		+
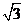
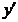
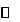
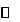
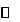
y		10.4				-10.4

Используя правило 1.1 нахождения локальных экстремумов с помощью первой производной

получаем. При х =- 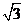локальный максимум, при х=0 экстремума нет, при х= 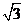локальный минимум.

5. Исследуем функцию на выпуклость. Для этого используем правило 1.2. Вычисляем вторую производную, приравниваем её нулю и находим точки «подозрительные на перегиб».

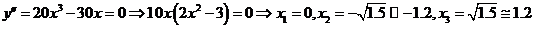
Вторая производная 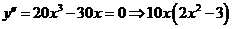положительна

на интервалах 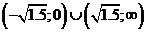Производная отрицательна на интервалах

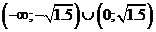.Определяем точки подозрительные на перегиб.

Вычисляем значения функции в точках подозрительных на перегиб

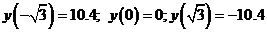и заполняем таблицу.

Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

x		-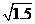
	-		+		-		+
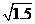
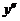
y		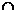-6.4				6.4

Используя правило 1.2 нахождения точек перегиба с помощью второй производной, получаем, что точки 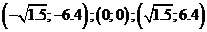являются точками перегиба графика функции.

6. Исследуем функцию на асимптотическое поведение. Многочлен не имеет асимптот.

7. График пересекает ось ОУ в точке (0,0).

8. Используя таблицы, строим график функции

Пример 1.2. Исследовать функцию 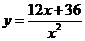и построить её график

1. Данная функция это дробно- рациональная функция. Область определения D есть множество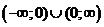

2. Определим нули функции. В данном случае это возможно

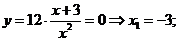
3.Функция общего вида

4. Определим участки монотонности и локальные экстремумы. Вычислим критические точки функции. В этих точках либо 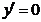, либо 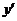не существует.

Вычисляем производную функции .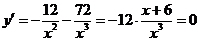

В точке 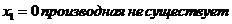. В точке .

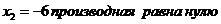Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

Производная 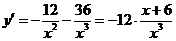положительна

на интервале 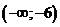. Производная отрицательна на интервалах

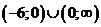. Вычисляем значения функции в критических точках.

В точке 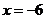, , 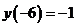в точке 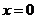значения функции не существует.

Заполняем таблицу.

x		-6
	+		-		-
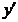
y		-1

Используя правило 1.1 (нахождения локальных экстремумов с помощью первой производной)

получаем. При 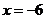локальный минимум, при х=0 экстремума нет.

5. Исследуем функцию на выпуклость. Для этого используем правило 1.2. Вычисляем вторую производную, приравниваем её нулю и находим точки «подозрительные на перегиб». Вторая производная равна 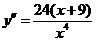. В точке 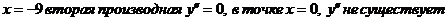. Точка подозрительная

на перегиб имеет координаты 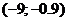. Определяем знаки 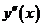на интервалах.

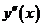положительна на интервалах 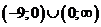. 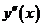отрицательна на интервале 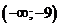. Согласно правилу 1.2 точка 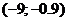является точкой перегиба графика.

Для определения знаков второй производной применяем метод интервалов и заполняем соответствующую таблицу

x		-9
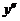
	-		+	нет	+
y		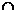-0,9		нет

6. Находим асимптоты графика функции. Асимптота это прямая, к которой неограниченно приближается график функции при 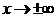. Наклонная асимптота имеет уравнение 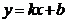. Алгоритм нахождения параметров 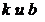известен.

Сначала определяем .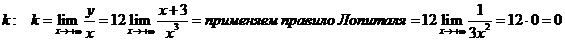

Затем определяем

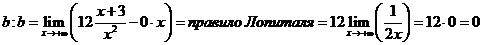
Уравнение наклонной асимптоты найдено .

При график также имеет асимптоту .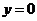

Легко находим, что 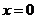есть уравнение вертикальной асимптоты

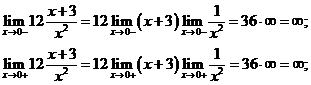
7. График не пересекает ось ОУ.

8. Используя таблицы, строим график функции

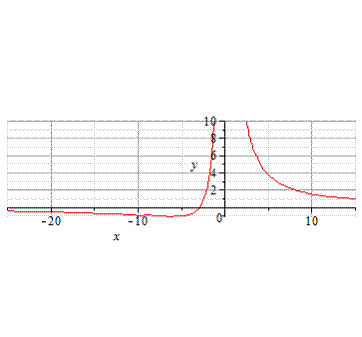
Пример 1.3. Исследовать функцию 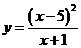и построить её график

1. Данная функция это дробно- рациональная функция. Область определения D есть множество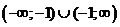

2. Определим нули функции. В данном случае это возможно

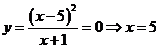
3.Функция общего вида.

4.с помощью первой производной определяем участки монотонности и локальные экстремумы. Вычисляем критические точки функции. Стационарными точками являются точки, в которых :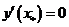

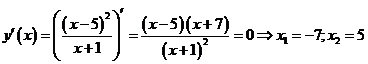
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

x		-7
	+		-		+
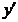
y		-24

Используя правило 1.1 нахождения локальных экстремумов получаем. При х=-7 локальный максимум, при х=5 локальный минимум.

5. С помощью второй производной 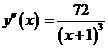исследуем функцию на выпуклость. Находим точки «подозрительные на перегиб»

Точки, в которых производная равна нулю отсутствуют 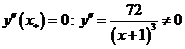. Точка, в которых вторая производная не существует .

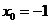Для определения знаков второй производной слева и справа от точки 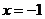применяем метод интервалов и заполняем соответствующую таблицу

x		-1
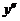
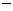
		нет	+
y		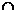нет

Точек перегиба графика нет.

6. Исследуем поведение функции на бесконечности.

Находим наклонную асимптоту. Асимптота это прямая, к которой неограниченно приближается график функции при 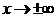. Наклонная асимптота имеет уравнение 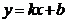. Алгоритм нахождения параметров 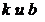известен. Сначала определяем .

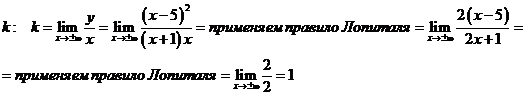Затем

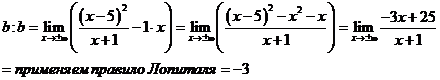
Уравнение наклонной асимптоты найдено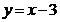

Проверим, имеет ли данная функция вертикальную асимптоту.

Прямая, имеющая уравнение 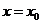называется вертикальной асимптотой графика функци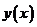и если 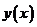бесконечно большая при .

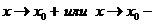Так как 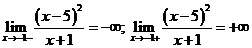, то

прямая 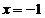является вертикальной асимптотой.

7.График пересекает ось ОУ в точке (5,0).

8. Строим график функции.

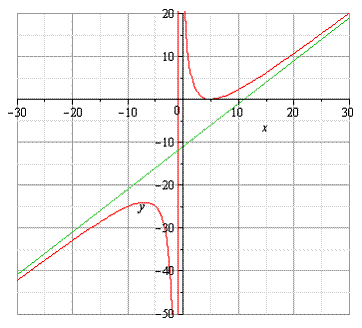
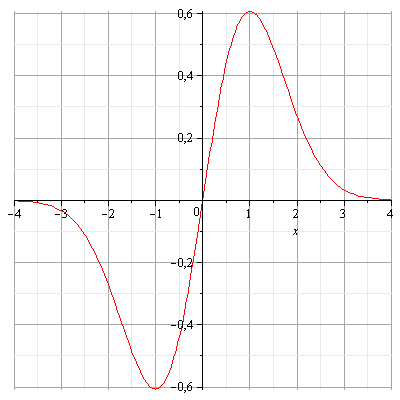
Пример 1.4. Исследовать функцию 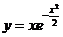и построить её график

1. Область определения D функции интервал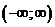

2.Определим нули функции. В данном случае это возможно

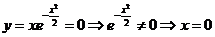
3.Так как 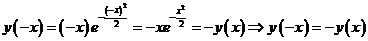, то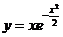

функция нечётная.

4.С помощью первой производной определяем участки монотонности и локальные экстремумы. Вычисляем критические точки функции. Такими точками являются точки в которых :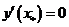

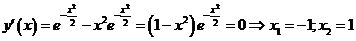
Для определения знаков производной применяем метод интервалов и заполняем соответствующую таблицу

x		-1
			+
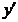
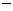
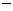
y		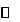-0,6		0,6

Используя правило 1.1 нахождения локальных экстремумов с помощью первой производной

получаем. При х=-1 локальный минимум, при х=1 локальный максимум.

5.С помощью второй производной исследуем функцию на выпуклость. Находим точки «подозрительные на перегиб».В этих точках 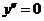или не существует

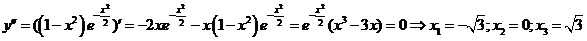
Для определения знаков второй производной слева и справа от этих точек применяем метод интервалов и заполняем соответствующую таблицу

x		-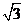
			+				+
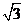
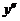
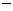
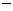
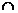
y		нет

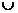
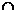
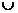
4. Исследуем функцию на асимптотическое поведение.

Находим наклонную асимптоту. Асимптота это прямая, к которой неограниченно приближается график функции при 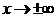. Наклонная асимптота имеет уравнение 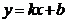. Алгоритм нахождения параметров 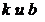известен

Сначала всегда определяем .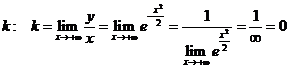

Затем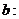

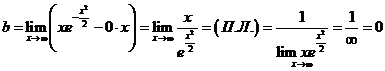
П. Уравнение наклонной асимптоты найдено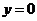

Так как функция 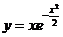непрерывна, то вертикальных асимптот нет.

7. График пересекает ось ОУ в точке (0,0).

8. Строим график функции.

Date: 2015-07-27; view: 418; Нарушение авторских прав