Понятие рекурсивных функций

Определение. Функции, которые могут быть получены из простейших о(x)=0, s(x)=x+1, I_n^m(x₁,...,x_n)=x применением конечного числа раз операторов суперпозиции, примитивной рекурсии и минимизации, называются рекурсивными.

Класс рекурсивных функций шире класса примитивно рекурсивных функций хотя бы по тому, что он содержит не только всюду определённые функции. Докажем, например, что функция

является рекурсивной. Действительно, f(x,y)=min(z|y+z=x), а ранее было установлено, что функция u(x,y)=x+y примитивно рекурсивна.

Рекурсивные функции отражают наше интуитивное представление о функциях, вычислимых некоторым механическим устройством. В частности, они вычислимы на машинах Тьюринга. Наоборот, всякая функция, вычислимая на машине Тьюринга является рекурсивной. Мы не будем проверять этот факт, так как это потребовало бы слишком много времени и места.
Отметим, что не всякая функция натуральных аргументов является рекурсивной, даже не всякая функция одного аргумента. Существование нерекурсивных функций и является "математической причиной" наличия алгоритмически неразрешимых задач.

Приступим к построению класса рекурсивных функций в соответствии с изложенными принципами. Напомним, что рассматриваются функции, заданные на множестве натуральных чисел и принимающие натуральные значения. Функции предполагается брать частичные, т. е. определенные, вообще говоря, не для всех значений аргументов. В качестве исходных простейших функций выберем следующие:

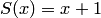(функция следования);
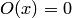(нуль-функция);
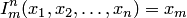(функции-проекторы, ).

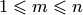Вычислимость (более того, правильная вычислимость) этих функций с помощью машины Тьюринга установлена в примерах 32.7 и 32.10. Далее, в качестве операторов, с помощью которых будут строиться новые функции, выберем следующие три: операторы суперпозиции, примитивной рекурсии и минимизации.

Определение 33.1 (оператор суперпозиции). Будем говорить, что n-местная функция 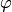получена из m-местной функции 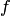и n-местных функций 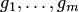с помощью оператора суперпозиции, если для всех 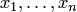, справедливо равенство:

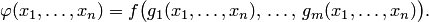
Понятие суперпозиции функций и сложной функции хорошо известно, но нас сейчас этот оператор интересует с точки зрения его взаимоотношений с процессом вычислимости функций с помощью машин Тьюринга.

Теорема 33.2. Если функции 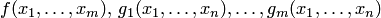правильно вычислимы по Тьюрингу, то правильно вычислима и сложная функция (суперпозиция функций):

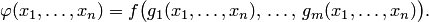
Определение 33.3. Говорят, что (n+1)-местная функция 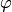получена из n-местной функции 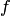и (n +2)-местной функции 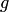с помощью оператора примитивной рекурсии, если для любых 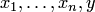справедливы равенства:

Пара этих равенств называется схемой примитивной рекурсии.

Здесь важно отметить то, что, независимо от числа аргументов в 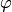, рекурсия ведется только по одной переменной 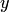; остальные 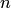переменных 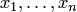, на момент применения схемы примитивной рекурсии зафиксированы и играют роль параметров. Кроме того, схема примитивной рекурсии выражает каждое значение определяемой функции 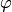не только через данные функци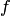и и 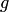, но и через так называемые предыдущие значения определяемой функции 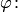прежде чем получить значение 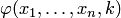, придется проделать 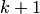вычисление по указанной схеме — для .

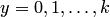Определение 33.4. Функция называется примитивно рекурсивной, если она может быть получена из простейших функций 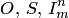с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии.

Наконец, введем заключительный, третий, оператор.

Определение 33.5 (оператор минимизации). Будем говорить, что n-местная функция 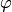получается из (n+1)-местных функци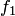й и 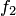с помощью оператора минимизации, или оператора наименьшего числа, если для любых 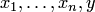равенство 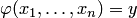выполнено тогда и только тогда, когда значения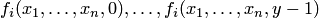 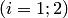определены и попарно неравны:

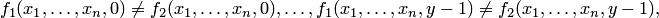
а 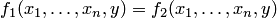. Коротко говоря, величина равна наименьшему значению аргумента 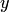, при котором выполняется последнее равенство. Используется следующее обозначение:

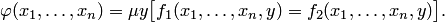
В частном случае может быть 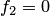. Тогда 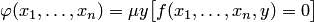. Оператор минимизации называется также µ-оператором. Этот оператор предназначен для порождения следующего важного класса рекурсивных функций.

Определение 33.6. Функция называется частично рекурсивной, если она может быть получена из простейших функций 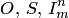с помощью конечного числа применений суперпозиции, примитивной рекурсии и µ-оператора. Если функция всюду определена и частично рекурсивна, то она называется общерекурсивной. (Отметим, что не всегда частично рекурсивную функцию можно эффективно доопределить до общерекурсивной.)

Ясно, что всякая примитивно рекурсивная функция будет и частично рекурсивной (и даже общерекурсивной, так как каждая примитивно рекурсивная функция всюду определена), поскольку для построения частично рекурсивных функций из простейших используется больше средств, чем для построения примитивно рекурсивных функций. В то же время класс частично рекурсивных функций шире класса примитивно рекурсивных функций, так как все примитивно рекурсивные функции всюду определены, а среди частично рекурсивных функций встречаются и функции не всюду определенные.

Понятие частично рекурсивной функции оказалось исчерпывающей формализацией понятия вычислимой функции. При построении аксиоматической теории высказываний исходные формулы (аксиомы) и правила вывода выбирались так, чтобы полученные в теории формулы исчерпали бы все тавтологии алгебры высказываний. К чему же стремимся мы в теории рекурсивных функций, почему именно так выбрали простейшие функции и операторы для получения новых функций? Рекурсивными функциями мы стремимся исчерпать все мыслимые функции, поддающиеся вычислению с помощью какой-нибудь определенной процедуры механического характера. Подобно тезису Тьюринга, в теории рекурсивных функций выдвигается соответствующая естественно-научная гипотеза, носящая название тезиса Чёрча:

Числовая функция тогда и только тогда алгоритмически (или машинно) вычислима, когда она частично рекурсивна.

Date: 2015-07-27; view: 1289; Нарушение авторских прав