п°3.3 Примеры решения задач на построение методом подобия

Стоит отметить, что при решении задач на построение этим методом часто бывает целесообразно объединять этапы «Анализ» и «Построение». Так как любое по­добие есть композиция некоторого движения и гомотетии, мы будем поль­зоваться при решении задач методом подобия гомотетией.

Задача №1 (Метод подобия)

Построить общую касательную к двум данным окружностям.

1) АНАЛИЗ

Предположим, что задача решена и l – общая касательная к окружностям 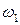и 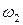(рис. 12), тогда 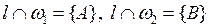. Проведем (О₁О₂) – линия центров,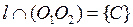

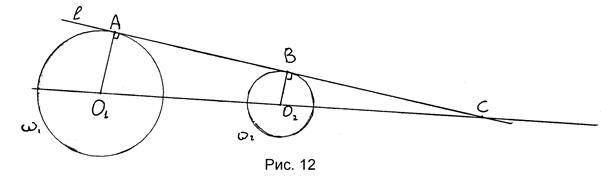Рассмотрим треугольники АО₁С и ВО₂С: угол С – общий, О₁АС = О₂ВС = 90⁰, так как радиус, проведенный в точку касания, перпендикулярен к касательной, следовательно треугольники АО₁С и ВО₂С подобны. Отсюда 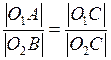, а так как 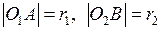, то 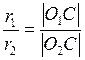. Значит точка С делит отрезок [О₁О₂] в отношении r₁: r₂ и является центром подобия. Таким образом, для построения касательной l, общей к окружностям 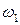и 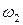, необходимо построить касательную, проходящую через эту точку к одной из окружностей, которая также будет являться касательной и ко второй окружности.

2) ПОСТРОЕНИЕ (Рис. 13)

Строим:

1. (О₁О₂) – линия центров

2. [АВ]: [АВ] – диаметр 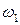и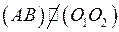

3. [А₁В₁]: [А₁В₁] – диаметр ,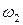

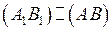
4. (АВ₁), (АА₁)

5. ,

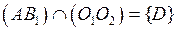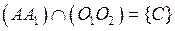
С, D – центры подобия.

6. l₁: l₁ – касательная к ,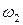

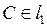
7. l₂: l₂ – касательная к ,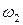

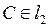
8. l₃: l₃ – касательная к ,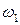

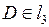
9. l₄: l₄ – касательная к ,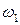

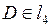
l₁, l₂, l₃, l₄ – искомые касательные.

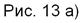
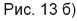
3) ДОКАЗАТЕЛЬСТВО

а) l₁ (l₂) – касательная к 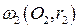по построению. Докажем, что l₁ (l₂) является также касательной к .

Так как С – центр подобия окружносте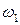й и 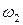, то существует гомотетия с центром в точке С, переводящая окружность 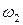в 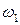: 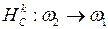. Следовательно, .

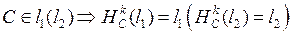Так как l₁ (l₂) касается окружности 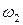, то ее образ (та же прямая) касается окружности 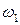, то есть l₁, l₂ – искомые касательные.

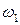б) l₃ (l₄) – касательная к по построению. D – центр подобия и 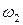, следовательно:

, .

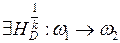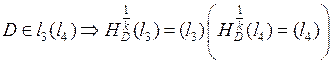Так как l₃ (l₄) касается окружности 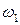, то ее образ (та же прямая) касается 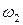, то есть l₃, l₄ – искомые касательные.

4) ИССЛЕДОВАНИЕ

Если О₁ = О₂, то задача имеет бесконечное множество решений при r ₁ = r ₂, либо не имеет решений при r ₁ ≠ r ₂.

Рассмотрим случай, когда О₁ ≠ О₂:

1. r ₁ ≠ r ₂. Пусть для определенности r ₁ > r ₂.

Из анализа следует, что любая общая касательная окружносте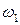й и 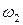проходит через из центров подобия. Из доказательства следует, что если прямая проходит через центр подобия и касается одной окружности, то она касается и другой. Таким образом, число решений определяется числом всех касательных, проходящих через центр подобия и касающихся одной из окружностей.

а) |О₁О₂| > r ₁ + r ₂ задача имеет 4 решения;

б) |О₁О₂| = r ₁ + r ₂ задача имеет 3 решения;

в) |О₁О₂| < r ₁ + r ₂ или |О₁О₂| > r ₁ - r ₂ задача имеет 2 решения;

г) |О₁О₂| = r ₁ - r ₂ задача имеет 1 решение;

д) |О₁О₂| < r ₁ - r ₂ решений нет.

2. r ₁ = r ₂. В этом подслучае задача всегда имеет 4, 3, или 2 решения.

§4. Алгебраический метод решения задач на построение.

При решении задач на построение алгебраическим методом решение задачи сводят к построению некоторого отрезка, длину которого выражают через длины данных отрезков с помощью некоторой формулы. Анализ при решении алгебраическим методом сводится к нахождению этой формулы, а также к выяснению, какими простейшими построениями нужно воспользоваться, чтобы построить отрезок по полученной формуле. Алгебраический метод является универсальным. С его помощью можно решить любую раз­решимую задачу на построение, но из-за громоздких выкладок его следует применять лишь к тем задачам, которые не поддаются решению другими методами.

При решении задач на построение алгебраическим методом использу­ются следующие простейшие построения отрезков, заданных формулами, где a,b,c,d - длины данных отрезков, х - длина искомого отрезка:

1. х = a + b;

2. х = a – b, где а > b;

3. х = n∙a, где n – натуральное число;

4. 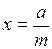, где m – натуральное;

5. 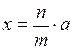, где n, m – натуральные;

6. ;

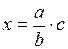7. ;

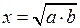8. ;

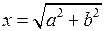9. 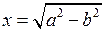, где а > b;

Построения отрезков по формулам 1 - 9 считаются известными, к ним сводятся построения по более сложным формулам, и при решении задачи они просто выполняются, но не описываются.

Построение отрезков по формулам 1 - 5 и 8 - 9 очевидны. Остано­вимся более подробно на построениях отрезков по формулам 6 и 7.

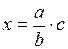- построение четвертого пропорционального

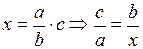. Для построения отрезка воспользуемся теоремой Фалеса.

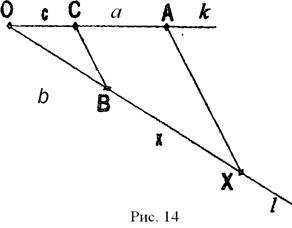Строим:

1. k, l – два луча с общим началом О;

2. С, ;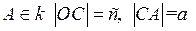

3. ;

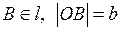4. (СВ);

5. ;

6. [ВХ] – искомый отрезок. |ВХ| = х.

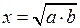- построение среднего геометрического длин отрезков а и b.

Строим:

1. Луч l с началом А;

2. ;

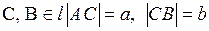3. О – середина [АВ];

4. ;

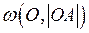5. ;

6. ;

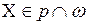7. [СХ] – искомый отрезок. |СХ| = х.

Докажем, что полученный отрезок действительно искомый.

[СХ] – высота, проведенная из вершины прямого угла треугольника АХВ. Как известно |СХ|² = |АС|∙|СВ| = а∙b, |СХ| = 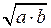= х, следовательно [СХ] – искомый отрезок.

Задача.

От данного квадрата отсечь равные прямоугольные треугольники так, чтобы получился правильный восьмиугольник.

1) АНАЛИЗ

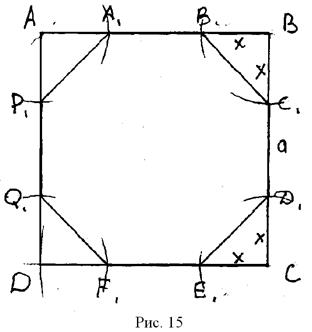Предположим задача решена и восьмиугольник А₁В₁С₁D₁E₁F₁P₁Q₁ – искомый, то есть у него все стороны равны (рис. 15). Пусть прямоугольные треугольники, которые надо отсечь – AA₁P₁, B₁BC₁, D₁CE₁, F₁DQ₁. Так как нам не сказано ничего о катетах прямоугольных треугольников, то будем считать, что треугольники равнобедренные. Тогда обозначим через х – сторону такого треугольника. D₁C = CE₁ = х, тогда сторона восьмиугольника |D₁E₁| = 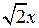. Теперь рассмотрим сторону квадрата [ВС] и обозначим ее длину через а, тогда сторона восьмиугольника |D₁C₁| = а - 2 х. Но так как восьмиугольник правильный, то |D₁E₁| = |D₁C₁|, 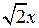= а - 2 х. Преобразовав формулу:

Построив х и отложив от каждой вершины на каждой из сторон квадрата, получим искомый восьмиугольник.

2) ПОСТРОЕНИЕ (Рис. 16)

Строим:

1. [ОЕ) и [OF) – два луча с общим началом О;

2. [ОК]: |ОК| = 2 а, К [ОЕ);

3. 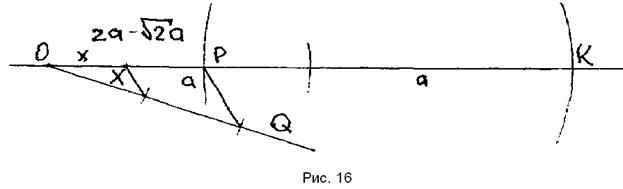[РК]: |РК| = 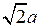, Р [ОЕ);

|ОР| = 2 а -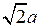

4. [ОХ]: |ОХ| = ½|ОР|

[ОХ] – искомый. |ОХ| = х.

5. [АА₁] = [ВВ₁] = [ВС₁] = [СD₁] = [CE₁] = [DF₁] = [DQ₁] = [AP₁] = x, где А₁, В₁ [АВ]; С₁, D₁ [ВС]; E₁, F₁ [СD]; Q₁, P₁ [АD]

А₁В₁С₁D₁E₁F₁P₁Q₁ – искомый.

3) ДОКАЗАТЕЛЬСТВО

Оно следует из анализа и построения.

4) ИССЛЕДОВАНИЕ

Так как отрезок по заданной формуле всегда можно построить, то задача всегда имеет решение, причем единственное.

Заключение.

Рассмотренные в курсовой работе задачи на построение являются достаточно сложными для ученика средней школы, но, тем не менее, могут быть с легкостью рассмотрены как дополнительный материал при изучении этой темы на уроке.

Геометрические построения не связаны непосредственно с наиболее актуальными проблемами математики. Но в процессе их изучения усваиваются понятия и приобретаются некоторые навыки, имеющие значение и за пределами этого вопроса.

В завершении хочется отметить, что я не стал рассматривать такие вопросы, как разрешимость задачи на построение, построение с помощью одного циркуля или линейки, теоремы конструктивной геометрии и т. д., поскольку не ставил своей целью создать некий учебник по построению циркулем и линейкой. За более обширным теоретическим курсом можно обратиться к книгам, которые указаны в списке литературы.

Литература

1. Аргунов Б.И. и Балк М.Б. Геометрические построения на плоскости. – М.:УЧПЕДГИЗ, 1952,268с.

2. Лотарева И.В., Ершов Д.А. Методика решения задач на построение (В помощь студентам очного и заочного отделений) Курск: КГУ, 2001, 38с.

3. Четверухин Н.Ф. Методы геометрических построений. – М.: УЧПЕДГИЗ, 1952, 146с.

4. Глаголев Н.А. Сборник геометрических задач на построение. – М.: 1903

5. Александров И.И. Сборник геометрических задач на построение. – М.: УЧПЕДГИЗ, 1950, 226с.

Date: 2015-07-27; view: 2744; Нарушение авторских прав